这里来一发需要开毒瘤优化，并且几率很小一遍过的模拟退火题解...

友情提醒：如果你很久很久没有过某一个点，您可以加上特判

可以像 P1337 [JSOI2004]平衡点 / 吊打XXX 那道题目一样

如果不会退火可以拿那道题练手...

个人看来这题和那题差不多，主要区别在get_ans()的函数上面

如何get_ans呢？
（图很垃圾，别介意）
先看这张图：

假设中间的黑点是目前确定的圆心，要get的ans是离这个点最远的圆上的点

那么初中数学老师就会教你：距离=两个圆心的距离+选中圆的半径

像这样：

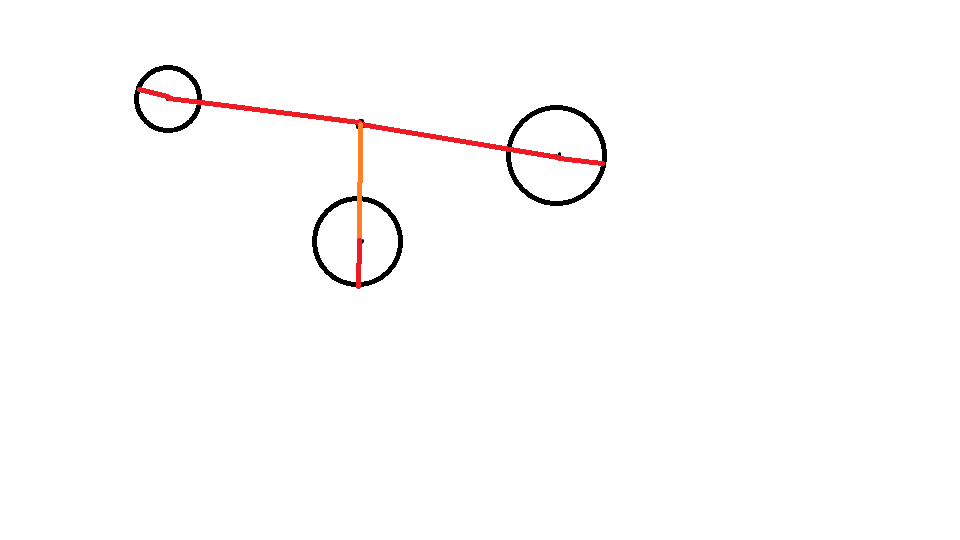
显然最远的点只要O（n）遍历取最大值就好了

然后套上退火的模板就好了吧

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("inline")
#pragma GCC optimize("Ofast")
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib> 
#include<ctime>
using namespace std;
inline int read(){
    int ans=0,f=1; char chr=getchar();
    while(!isdigit(chr)){if(chr=='-') f=-1;chr=getchar();}
    while(isdigit(chr)) {ans=(ans<<3)+(ans<<1)+chr-48;chr=getchar();}
    return ans*f;
}
int n;
double x[50005],y[50005],z[50005],ansx,ansy,BR;
double dis(double x,double y,double a,double b){return sqrt((x-a)*(x-a)+(y-b)*(y-b));}
double get(double q,double p){
    double ans=0;
    for(register int i=1;i<=n;++i)
        ans=max(dis(x[i],y[i],q,p)+z[i],ans) ;
    return ans;
}
const double delta=0.999;
double ans=1e20,maxn=-54564564;
int lim;
void Fire(){
    register double fx=ansx,fy=ansy;
    register double t=12180.0;
    while(t>1e-14){
        register double tx=fx+(rand()*2-RAND_MAX)*t;
        register double ty=fy+(rand()*2-RAND_MAX)*t;
        register double tans=get(tx,ty);
        register double DE=tans-ans;
        if(DE<0){
            fx=tx;
            fy=ty;
            ansx=tx;
            ansy=ty;
            ans=tans;
        }else if(exp(-DE/t)*RAND_MAX>rand())
            fx=tx,fy=ty;
        t*=delta;
        if(clock()-BR>=lim){printf("%.7lf %.7lf %.7lf",ansx,ansy,ans);exit(0);}
    }       
}
int main(){
    BR=clock();
    srand(unsigned(time(0)));
    n=read();
    for(register int i=1;i<=n;++i)  scanf("%lf%lf%lf",&x[i],&y[i],&z[i]),ansx+=x[i],ansy+=y[i],maxn=max(maxn,z[i]);
    ansx/=1.0*n;
    ansy/=1.0*n;
    lim=(n<=1000||maxn==0)?995:3995;
    lim*=1000;
    while(1) Fire();
    return 0;
}