描述
题目描述
首先我们把题目抽象一下,说我们的密码是一个对称的密码,那么很简单呀,我们可以直接考虑一下其实这个题目的含义是不是就是我们可以删除前缀或者是后缀,然后问我们的最长回文子串
题解
解法一:动态规划
实现思路
首先这个题目既然上面标注了是动态规划的题目,那么我们就是可以向着动态规划的角度来考虑这个问题
然后我们这里使用一个最为直白的动态规划的方法
首先我们先确定这么一个思路:回文串两边加上两个相同字符,会形成一个新的回文串
比如:

那么我们的方法就是建立一个二维数组, 然后我们找出来所有的回文子串
dp[i][j]记录子串i--j是否为回文串
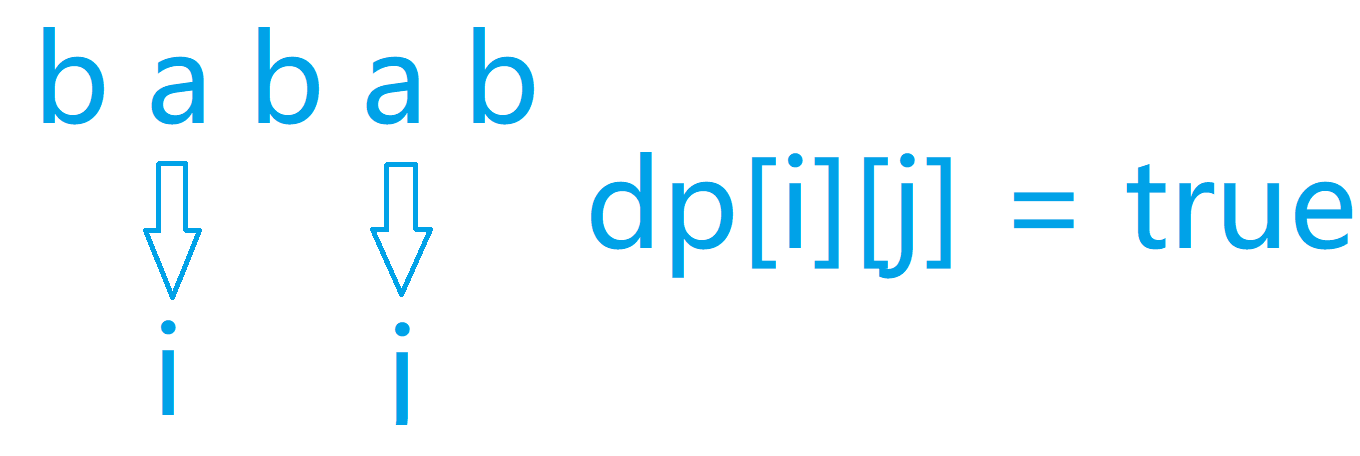
然后我们还可以知道, 单个字符本身就是一个回文串所以
然后我们可以得到递推关系式:
if (s[i] == s[j] && dp[i + 1][j - 1] == true) dp[i][j] = true;
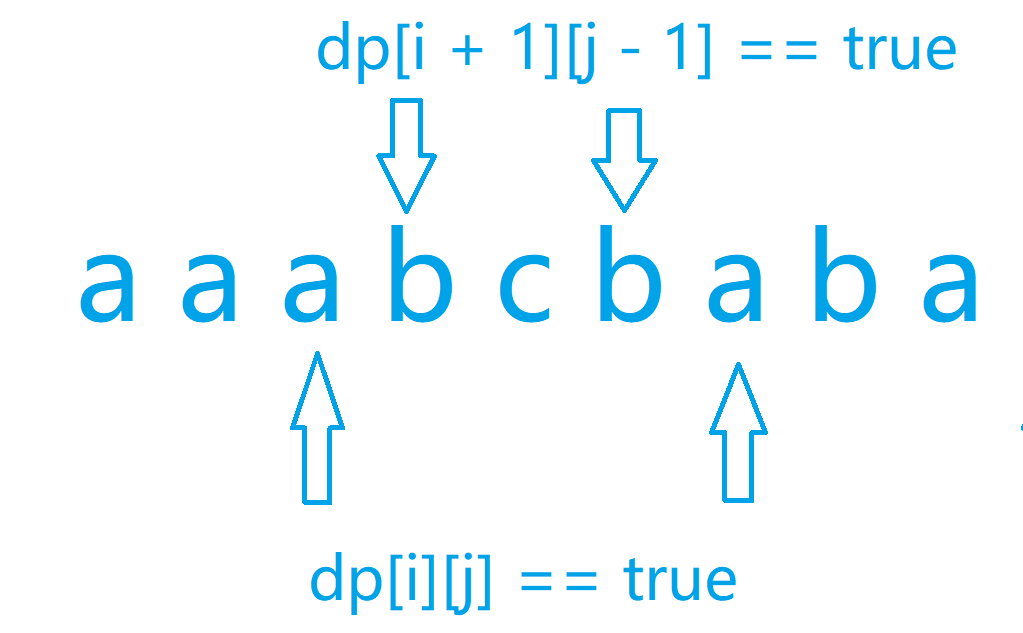
然后我们仍然是需要注意我们边界问题, 就是只有时的时候有效
然后我们迭代的过程需要反序迭代变量, 正向迭代
最后上面的递推方程和方向问题都确定好了之后, 我们可以去考虑初始化的问题了
- 一开始所有的地方都是false
- 对角线时true
- 自对角线右下角开始, 自下而上, 自左而右而进行递推
代码实现
#include <bits/stdc++.h>
using namespace std;
signed main() {
string s;
while (cin >> s) {
int n = s.size();
vector<vector<bool>> dp(n, vector<bool> (n, 0));
for (int i = 0; i < n; i++) dp[i][i] = true;
// 初始化我们的dp数组
int res = 1;
// 我们的最大的回文子串的长度
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (s[i] == s[j]) {
if (j - 1 >= i + 1) {
// 子串s[i + 1 ... j - 1]保证有效性
if (dp[i + 1][j - 1]) dp[i][j] = true;
} else {
// 此时的j < i + 2 即 j <= i + 1
// 再之 s[i] == s[j] 肯定是回文
dp[i][j] = true;
}
}
if (dp[i][j]) {
// 更新的最大长度
res = max(res, j - i + 1);
}
}
}
cout << res << "\n";
}
return 0;
}
时空复杂度分析
时间复杂度:
理由如下: 其实我们就是两重循环
空间复杂度:
理由如下: 其实我们这里是假设编译器正常运行没有任何优化, 在某些条件下我们的编译器会把我们的的空间优化成类似于的空间复杂度, 但是这里我们只考虑一般的普遍的情况
解法二:Manacher算法
相关题目
裸的板子题: 最长回文子串
相关题解: 牛客我的博客
实现思路
我们想要求取最长回文子串的话, 我们这里给出专门解决这个问题的一个方法就是算法, 当然我们也可以使用二分加哈希或者后缀数组和快速来做, 但是这里我们引入一个时间和空间上有更小常数的算法
首先我们可以肯定的第一点就是我们的字符串一共是两种, 一种是偶数串, 一种是奇数串, 这给我们求取最长回文子串造成了困难, 那么我们可以把我们的偶数串和奇数串统一变成奇数串, 如何实现呢? 如图所示

我们可以保证这个字符串就是奇数长度的
然后我们可以得到转换过后的一个性质: 长度的回文串转换后得到的回文串半径为
然后我们记录指以为中心的最大回文串的半径长度
我们求取: 从前向后遍历, 同时维护一个有边界最靠右的回文串, 记录其和递推到时, 找关于的对称点, 有这么一个图参考
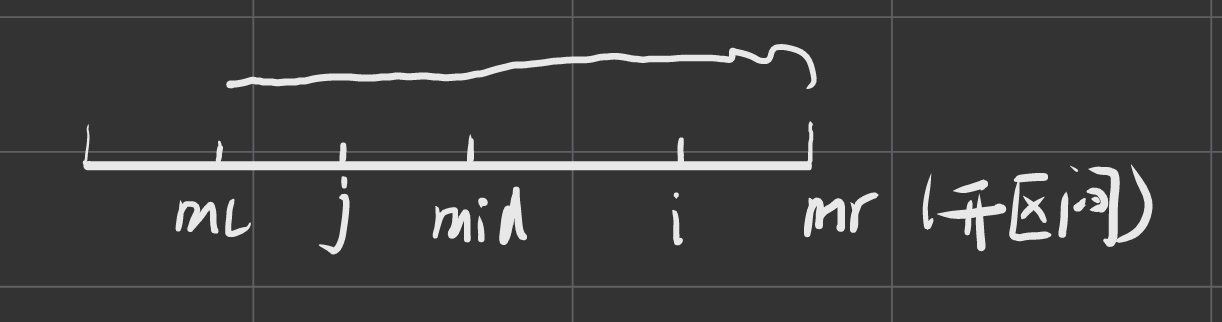
如果我们的在之间,
若我们的在处, 然后我们暴力扩张同时更新
然后我们可以书写我们的代码了
代码实现
#include <bits/stdc++.h>
using namespace std;
string init(string &s) {
string res = "";
res += "$#";
for (int i = 0; i < s.size(); i++) res += s[i], res += '#';
res += '^';
return res;
// 这个是在开始和结束加上通配符, 然后我们中间每个分割的地方加上#
}
void manacher(vector<int> &p, string &s) {
int mr = 0, mid;
// mr代表以mid为中心的最长回文的有边界
// mid为i和j的中心点, i以mid为对称点翻折到j的位置
for (int i = 1; i < s.size(); i++) {
if (i < mr)
p[i] = min(p[mid * 2 - i], mr - i);
// 2 * mid - i为i关于mid的对称点
else
p[i] = 1;
// 超过边界总共就不是回文了
while (s[i - p[i]] == s[i + p[i]]) p[i]++;
// 不需要判断边界, 因为我们有通配符
if (i + p[i] > mr) {
mr = i + p[i];
mid = i;
}
// 我们每走一步i, 都要和mx比较, 我们希望mx尽可能的远
}
}
signed main() {
string s;
while (cin >> s) {
cin >> s;
s = init(s);
vector<int> p(s.size());
manacher(p, s);
// 初始化字符串和求取出来我们的每一个位置的最长长度
int maxx = INT_MIN;
for (auto &it : p) maxx = max(maxx, it);
cout << maxx - 1 << "\n";
}
return 0;
}
时空复杂度分析:
时间复杂度:
理由如下: 我们的内层循环有两种情况, 如果我们的在内部, 我们的次数是小于等于的, 如果在边界, 那么我们向外扩张的时候右边界是单调的, 我们运行的过程中从不减少, 这个是线性的, 所以我们的时间复杂度就是的
空间复杂度:
理由如下: 我们其他地方也就是扩展了我们的字符串, 也就是扩展大概倍左右, 其实也是级别的






 京公网安备 11010502036488号
京公网安备 11010502036488号