一、关于浮点数与精度

这一部分，我们要明确c++的三种浮点类型，以及为什么会有精度误差，怎么降低精度误差。

float double 以及long double

随着计算机的发展，我们基本以及淘汰了 float，所以我们只讲 double 和 long double。（~~不会把？不会吧！不会还有人在用float吧！！~~），在 IEEE-754 标准中，规定 double 是 64bit，其中一个 bit 用于表示正负，11位用于表示科学计数法，剩下的表示内容，附上图片。

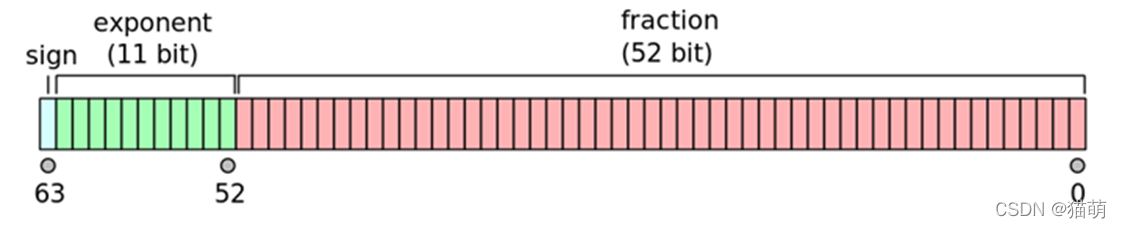
IEEE-754标准

由于在计算机内部是用二进制表示数字的，当我们要表示 $\dfrac{1}{4}$ 的时候，计算机可以用 $2^{- 2}$ 来表示。但是，当我们想表示 $\dfrac{1}{3}$ 的时候，计算机会采用 $2^{-2}+2^{-3}+2^{-4}+\cdots +2^{-\infty}$ ，按照极限理论，只要位数无限多，这两式子就相等。

那么问题来了，计算机只给了 52 位用于存储数据，我们就只能含泪丧失精度，在运算的时候这个损失还会进一步加大。在计算几何里，经常会有精度问题导致答案错误，为了降低精度误差，我们采用以下原则

能使用整数就不使用浮点数；
别用 float，视情况使用 long double；
减少数学函数的使用（如三角函数，开方）；
比较时加入容限；
尽量通过判定而非计算去得到答案（这里你可能看不懂，但我下面会讲一个例子来解释它）。

关于 long double，不同编译器实现不一样，而且跟编译器的位数有关，但一般都比 double 位数多,所以当精度达不到你预期的时候请开 long double。

二、关于除 0

请大家务必记住 double 运算中编译器是不会对你的除 0 操作进行报错的！请大家务必记住 double 运算中编译器是不会对你的除 0 操作进行报错的！请大家务必记住 double 运算中编译器是不会对你的除 0 操作进行报错的！重要的事情说三遍！在 double 类运算中，除以 0 一般会产生两种结果，一种是无穷数 inf，另一种是非数 NaN，具体如何触发请移步百度。下面是关于 NaN 的比较的一张表

在这里插入图片描述

可以看到，除了 == 操作，其他的操作都返回的 false。当你发现你的运行程序有一些奇怪的 bug 的时候，你应该排查下是否有除 0 问题。

3、关于模板

写计算几何板子必须高度可靠，请大伙努力尝试构建属于自己的板子，在理解的基础上有限度的使用别人的板子。

4、一些关于点，线，多边形你必须知道的基础知识

1、关于向量

向量的点积（Dot product）相信大家在中学都学过向量的点，这里就不做赘述。

向量的叉积（Cross product）叉积的几何意义为一条方向垂直两线平面大小，其大小为 $|\vec{a}| |\vec{b}| \sin \alpha$ 。，四指由 $\vec{a}$ 开始，指向 $\vec{b}$ ，拇指的指向就是 $\vec{a}\times \vec{b}$ 的方向，这一性质被称作 to-left 测试，是计算几何经常运用的向量性质之一。

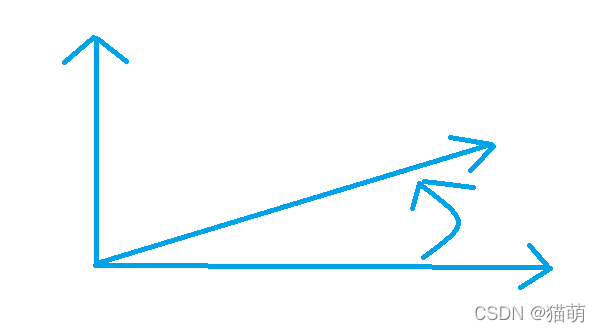
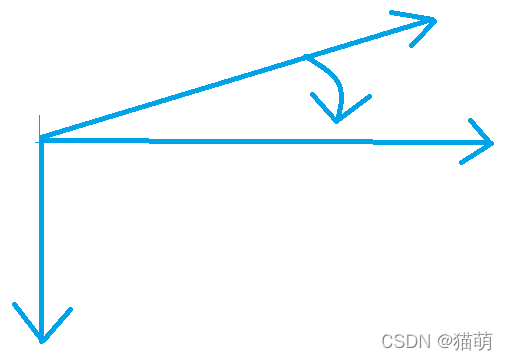
在这里插入图片描述

2、点，线的定义

我们通常这样子来定义线段和点

struc Point
{	
	double x,y;
}
struct Line
{
	Point s,v;
}

值得注意的是，由于计算几何中大量运用了向量的性质，在线以及线段的定义里，我们推荐使用的是用一个端点一个向量的方法来定义。

3、比较常见的点线关系判断以及线线关系判断

判断点与直线的关系 通过 to-letf 测试，我们可以得知，如果一个点不在直线上，那么该点与直线上任意一点的所连成的直线的向量（我们命名为 $\vec{a}$ ），与该直线的向量（我们命名为 $\vec{b}$ ）， $\vec{a}\times \vec{b}$ 的叉积不为0。反之我们判断其处于直线上。

判断点与线段的关系 我们先判断点是否处于直线上，在判断点的坐标是否处于线段的范围内，即可判断点是否处于直线
判断点与射线 同样的，我们先判断点是否处于与射线相同的直线上，然后利用向量叉积，注意是叉积的性质，来判断出发点到点构成的向量在射线上的投影，如果是负数就不处于，反之处于。
线线相交 直接 to-left 我相信你们懂的
线与线段相交 判断线段的两个端点是否在直线的两侧
线段与线段相交 这是一个重点，请手动画图去理解。为了加强理解我将先抛出一个错误的做法。假设给你直线AB,CD，按照上面线与线段相交的例子，那我们是不是可以分别判断 AB 在 CD 两侧，CD 在 AB 两侧，这样子我们就可以判断线段是否相交了。

考虑不到位

你没考虑以下特殊情况，即三点共线四点共线网上流传的做法是先进行快速排斥实验，再 AB、CD 互相判断是否在相互在直线两侧。快速排斥实验是用于快速判断两矩形是否相交的实验如下图

当以 AB、CD 为对角线的矩阵不相交的时候，那么两线段必然不相交，这包括了上面四点共线的特殊情况但是看看这代码量吧

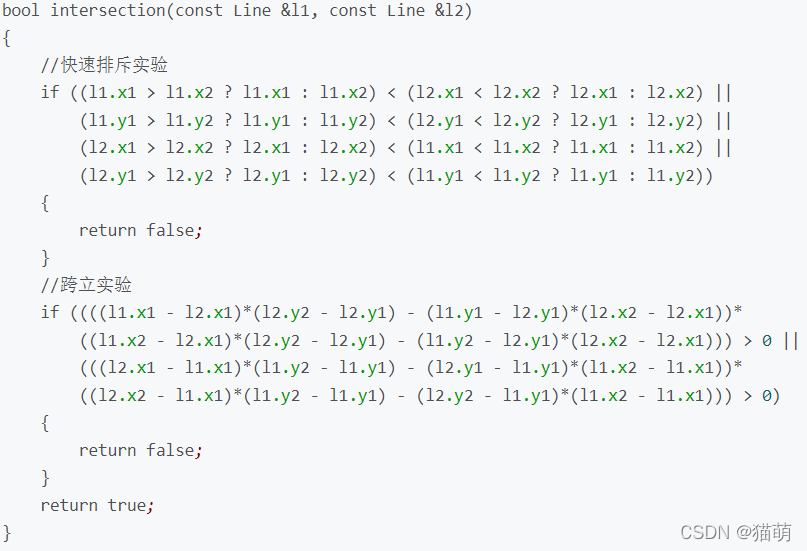
所以我们为什么不直接选择特判呢，当线段 $A$ 与 $B$ 处于同一直线的时候，看他们是否有一个端点在某另一个线段上，代量不就小多了。

求线与线，线与线段，线段与线段的交点 首先第一步要做的就是判断是否有交点。然后再求交，网上常用的是一般式求交点，代码长，计算多，一般都是用面积之比的方法推导出交点的式子俊杰老师用正弦推导了类似的的式子

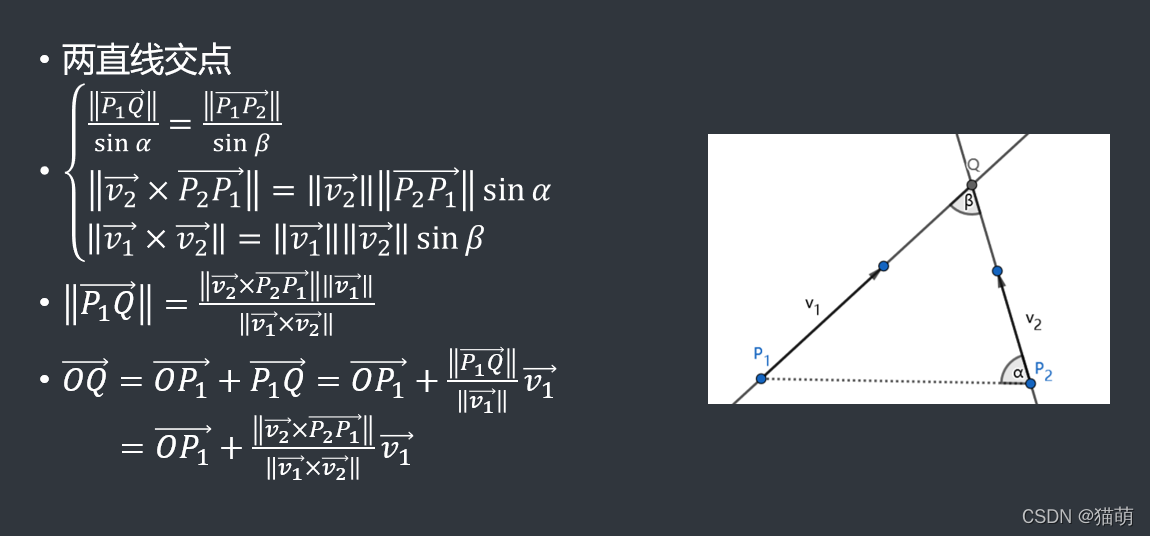
以上就是点与线，相关的练习可以看下方链接戳这里课程的第一章里其实还涉及到部分点与多边形的知识，同时也有对应的题目，其中讲了一个判断点在多边形内部的重要算法——光线回转法，对此我想专门写一个博客，到时候和关于牛客的练习的题解一起放出来，所以本博客到此为止。

如有想购买牛客计算几何的，戳这里链接后排推销其他牛客竞赛各类课程 dp 数学（强烈推荐）字符串（强烈推荐）数据结构

从0开始的计算几何（一）———点与线