描述

题目描述

给了我们一个二维数组, 和他的行和列, 给定我们一个值, 让我们在这个矩阵中找到等于这个值的横纵坐标, 并作为一个$vectorvector$返回

样例解释

样例输入

[[1,2,3],[4,5,6]],2,3,6

如图所示

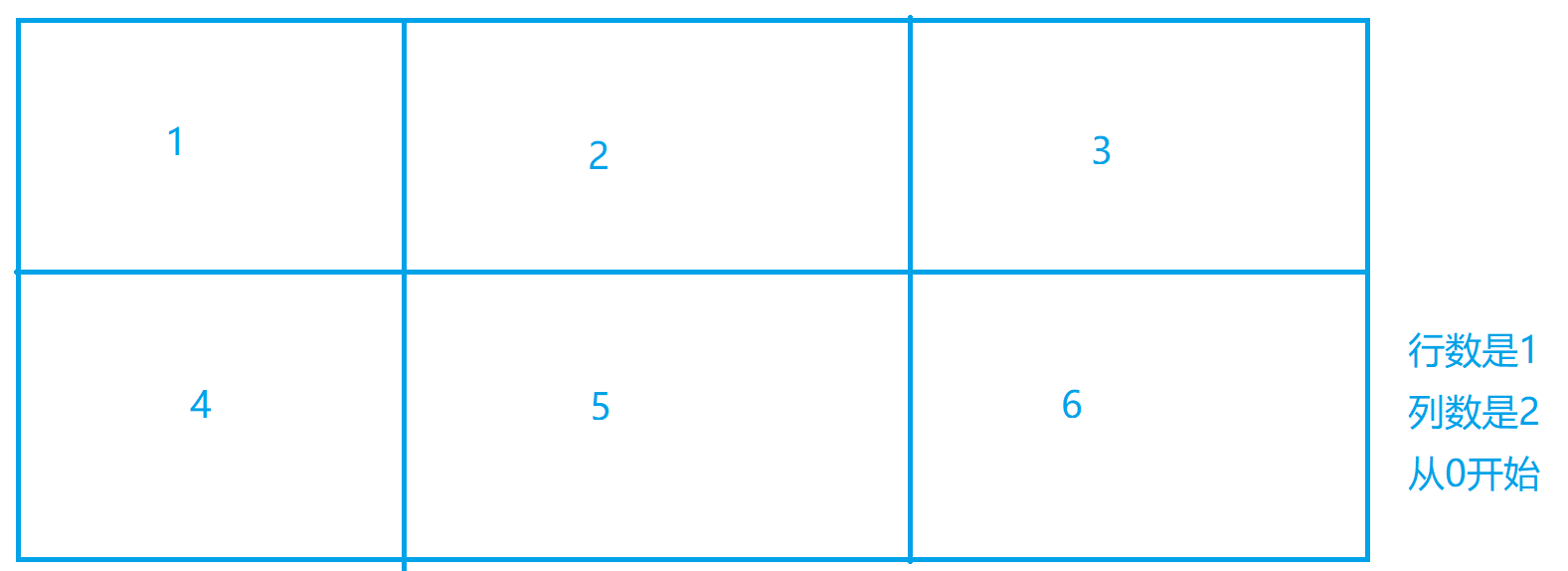
所以我们的样例输出就是

[1,2]

题解

解法一:

实现思路

我们可以直接暴力遍历我们的这个矩阵, 然后我们直接找到位置的时候返回

代码实现

class Solution {
   public:
    vector<int> findElement(vector<vector<int> > mat, int n, int m, int x) {
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                if (mat[i][j] == x) return {i, j};
//         遍历我们的循环，如果找到直接返回
        return {};
//         没有找到的话，就返回空
    }
};

时空复杂度分析

时间复杂度: $O(n\ast m)O(n\; *\; m)$

理由如下: 遍历了一个$n\ast mn\; *\; m$的矩阵

空间复杂度: $O(1)O(1)$

理由如下: 未使用额外空间

解法二:

实现思路

我们根据题意可以得知, 我们的这个矩阵的行和列都可以保证是从大到小的, 那么我们也就是要寻找这样的一个满足条件的行, 行的第一个元素要比$xx$小, 然后我们的最后一个元素一定要比$xx$大, 然后我们直接在这个行中二分查找我们第一个大于等于$xx$的位置, 然后判断这个位置的值是不是等于$xx$, 如果等于我们直接返回我们的横纵坐标

代码实现

class Solution {
   public:
    vector<int> findElement(vector<vector<int>> mat, int n, int m, int x) {
        for (int i = 0; i < n; i++) {
            if (*mat[i].begin() > x or mat[i].back() < x) continue;
//             如果这列的第一个比x大,或者最后一个比x小那么我们一定是不可以的
            int pos = lower_bound(mat[i].begin(), mat[i].end(), x) - mat[i].begin();
//             二分找到满足答案的位置
            if (mat[i][pos] == x) return {i, pos};
//             如果这个位置正好就是等于x,那么我们可以把这个位置返回
        }
        return {};
    }
};

时空复杂度分析

时间复杂度: $O(nlogm)O(nlogm)$

理由如下: 我们遍历了所有的行, 然后我们对每一行二分查找

空间复杂度: $O(1)O(1)$

理由如下: 我们未使用额外的空间