今日小结：今天上午考试考得不太好，第三题思路是对的，但不会写代码，第一题没开long long丢了30分，然后下午和晚上复习了LCA和负环的有关知识，但是做题有点少，所以准备明天再拿出一个小时来练习一下，明天的任务是拓扑排序和并查集。

一. 今日完成的题目：

洛谷P2912，洛谷P2971，洛谷P3884，洛谷P2136

二.

1. 当天完成题目数：4道。

2. 未完成6个题目的原因：上午考试了，时间不足

3. 复习的知识点：LCA，负环。

4.不会题目：洛谷P3398

三：

1. 洛谷P2912 牧场散步Pasture Walking

题目描述

The $N$ cows ($2 \leq N \leq 1,000$) conveniently numbered $1..N$ are grazing among the N pastures also conveniently numbered $1..N$. Most conveniently of all, cow i is grazing in pasture i.

Some pairs of pastures are connected by one of $N-1$bidirectional walkways that the cows can traverse. Walkway i connects pastures $A_i$and $B_i$ ($1 \leq A_i \leq N; 1 \leq B_i \leq N$) and has a length of $L_i$ ($1 \leq L_i \leq 10,000$).

The walkways are set up in such a way that between any two distinct pastures, there is exactly one path of walkways that travels between them. Thus, the walkways form a tree.

The cows are very social and wish to visit each other often. Ever in a hurry, they want you to help them schedule their visits by computing the lengths of the paths between $1 \leq L_i \leq 10,000$ pairs of pastures (each pair given as a query p1,p2 ($1 \leq p1 \leq N; 1 \leq p2 \leq N$).

POINTS: 200

有$N(2<=N<=1000)$头奶牛，编号为$1$到$W$，它们正在同样编号为$1$到$N$的牧场上行走.为了方便，我们假设编号为i的牛恰好在第$i$号牧场上.

有一些牧场间每两个牧场用一条双向道路相连，道路总共有$N - 1$条，奶牛可以在这些道路上行走.第i条道路把第Ai个牧场和第Bi个牧场连了起来($1 \leq A_i \leq N; 1 \leq B_i \leq N$)，而它的长度是 $1 \leq L_i \leq 10,000$.在任意两个牧场间，有且仅有一条由若干道路组成的路径相连.也就是说，所有的道路构成了一棵树.

奶牛们十分希望经常互相见面.它们十分着急，所以希望你帮助它们计划它们的行程，你只需要计算出Q(1 < Q < 1000)对点之间的路径长度•每对点以一个询问$p1,p2$ ($1 \leq p1 \leq N; 1 \leq p2 \leq N$). 的形式给出.

输入输出格式

输入格式：

Line 1: Two space-separated integers: $N$ and $Q$
Lines 2..N: Line i+1 contains three space-separated integers: $A_i, B_i$, and $L_i$
Lines $N+1..N+Q$: Each line contains two space-separated integers representing two distinct pastures between which the cows wish to travel: $p1$ and $p2$

输出格式：

Lines $1..Q$: Line i contains the length of the path between the two pastures in query $i$.

输入输出样例

输入样例#1：

输出样例#1：

2 
7

说明

Query $1$: The walkway between pastures $1$ and $2$ has length $2$.

Query $2$: Travel through the walkway between pastures $3$ and $4$, then the one between $4$ and 1, and finally the one between $1$ and $2$, for a total length of $7$.

思路：题意就是让你求树上两点之间的距离，我们可以先求出这两个点的$LCA$，然后发现它们之间的距离其实就是这两个点到根结点距离的和减去两倍的它们的$LCA$到根结点的距离。

代码：

#include<cstdio>
#include<algorithm>
#define maxn 1007
using namespace std;
int n,m,head[maxn],d[maxn],f[maxn][22],num,dis[maxn];
struct node {
  int v,w,nxt;
}e[maxn<<1];
inline void ct(int u, int v, int w) {
  e[++num].v=v;
  e[num].w=w;
  e[num].nxt=head[u];
  head[u]=num;
}
void dfs(int u, int fa) {
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(v!=fa) {
      f[v][0]=u;
      d[v]=d[u]+1;
      dis[v]=dis[u]+e[i].w;
      dfs(v,u);
    }
  }
}
inline int lca(int a, int b) {
  if(d[a]>d[b]) swap(a,b);
  for(int i=20;i>=0;--i) 
  if(d[a]<=d[b]-(1<<i)) b=f[b][i];
  if(a==b) return a;
  for(int i=20;i>=0;--i)
  if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
  return f[a][0];
}
int main() {
  scanf("%d%d",&n,&m);
  for(int i=1,u,v,w;i<n;++i) {
    scanf("%d%d%d",&u,&v,&w);
    ct(u,v,w);ct(v,u,w);
  }
  dfs(1,0);
  for(int j=1;j<=20;++j)
  for(int i=1;i<=n;++i)
  f[i][j]=f[f[i][j-1]][j-1];
  for(int i=1,u,v;i<=m;++i) {
    scanf("%d%d",&u,&v);
    printf("%d\n",dis[u]+dis[v]-2*dis[lca(u,v)]);
  }
  return 0;
}

2. 洛谷P2971 牛的政治Cow Politics

题目描述

Farmer John's cows are living on $N (2 \leq N \leq 200,000)$different pastures conveniently numbered $1..N$. Exactly $N-1$ bidirectional cow paths (of unit length) connect these pastures in various ways, and each pasture is reachable from any other cow pasture by traversing one or more of these paths (thus, the pastures and paths form a graph called a tree).

The input for a particular set of pastures will specify the parent node $P_i (0 \leq P_i \leq N)$ for each pasture. The root node will specify parent $P_i == 0$, which means it has no parent.

The cows have organized K$ (1 \leq K \leq N/2)$ different political parties conveniently numbered $1..K$. Each cow identifies with a single

political party; cow i identifies with political party $A_i (1 \leq A_i \leq K)$. Each political party includes at least two cows.

The political parties are feuding and would like to know how much 'range' each party covers. The range of a party is the largest distance between any two cows within that party (over cow paths).

For example, suppose political party $1$ consists of cows $1, 3$, and $6$, political party $2$ consists of cows $2, 4$, and $5$, and the pastures are connected as follows (party 1 members are marked as -$n$-):

$-3- | -1- / | \ 2 4 5$

$| -6-$ The greatest distance between any two pastures of political party $1$ is $3$ (between cows $3$ and $6$), and the greatest distance for political party 2 is 2 (between cows $2$ and $4$, between cows $4$ and $5$, and between cows $5$ and $2$).

Help the cows determine party ranges.

TIME LIMIT: $2$ seconds

MEMORY LIMIT: $64$MB

农夫约翰的奶牛住在$N (2 \leq N \leq 200,000)$片不同的草地上，标号为$1$到$N$。恰好有$N-1$条单位长度的双向道路，用各种各样的方法连接这些草地。而且从每片草地出发都可以抵达其他所有草地。也就是说，这些草地和道路构成了一种叫做树的图。输入包含一个详细的草地的集合，详细说明了每个草地的父节点$P_i (0 \leq P_i \leq N)$。根节点的$P_i == 0$, 表示它没有父节点。因为奶牛建立了$1$到$K$一共$K (1 \leq K \leq N/2)$个政党。每只奶牛都要加入某一个政党，其中，第i只奶牛属于第$A_i (1 \leq A_i \leq K)$个政党。而且每个政党至少有两只奶牛。这些政党互相吵闹争。每个政党都想知道自己的“范围”有多大。其中，定义一个政党的范围是这个政党离得最远的两只奶牛（沿着双向道路行走）的距离。

输入输出格式

输入格式：

Line $1$: Two space-separated integers: $N$ and $K$
Lines $2..N+1$: Line $i+1$ contains two space-separated integers: $A_i$ and $P_i$

输出格式：

Lines $1..K$: Line i contains a single integer that is the range of party $i$.

输入输出样例

输入样例#1：

输出样例#1：

3 
2

思路：题意是让你求在树上每个政党的两点间的最远距离，我们可以考虑先把每个政党的最大深度的点找出来，然后$O(n)$更新每个政党两点间的最大值，这里还是要通过$LCA$求两点间的树上距离。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 200007
using namespace std;
int n,k,num,rt,head[maxn],f[maxn][22],d[maxn],dis[maxn>>1],a[maxn],b[maxn],c[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct Edge {
  int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
  e[++num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
void dfs(int u, int fa) {
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(v!=fa) {
      f[v][0]=u;
      d[v]=d[u]+1;
      dfs(v,u);
    }
  }
}
inline int lca(int a,int b) {
  if(d[a]>d[b]) swap(a,b);
  for(int i=20;i>=0;--i)
  if(d[a]<=d[b]-(1<<i)) b=f[b][i];
  if(a==b) return a;
  for(int i=20;i>=0;--i)
  if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
  return f[a][0];
}
int main() {
  n=qread(),k=qread();
  for(int i=1,u;i<=n;++i) {
    a[i]=qread(),u=qread();
    if(!u) {rt=i;continue;}
    ct(u,i);ct(i,u);
  }
  dfs(rt,0);
  for(int i=1;i<=n;++i) {
    if(d[i]>b[a[i]]) {
      c[a[i]]=i;
      b[a[i]]=d[i];
    }
  }
  for(int j=1;j<=20;++j)
  for(int i=1;i<=n;++i)
  f[i][j]=f[f[i][j-1]][j-1];
  for(int i=1;i<=n;++i) 
  dis[a[i]]=max(b[a[i]]+d[i]-2*d[lca(c[a[i]],i)],dis[a[i]]);
  for(int i=1;i<=k;++i)
  printf("%d\n",dis[i]);
  return 0;
}

3. 洛谷P3884 二叉树问题

题目描述

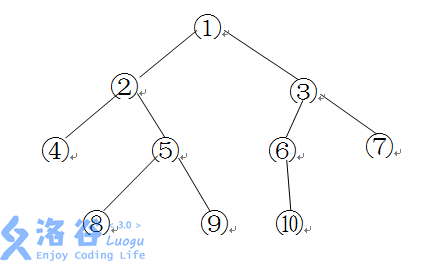
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：$4$ 宽度：$4$（同一层最多结点个数）

结点间距离： $⑧→⑥为8 (3×2+2=8)$

$⑥→⑦为3 （1×2+1=3）$

注：结点间距离的定义：由结点向根方向（上行方向）时的边数$×2$，

与由根向叶结点方向（下行方向）时的边数之和。

输入输出格式

输入格式：

输入文件第一行为一个整数$n(1≤n≤100)$，表示二叉树结点个数。接下来的$n-1$行，表示从结点$x$到结点$y$（约定根结点为$1$），最后一行两个整数$u、v$，表示求从结点$u$到结点$v$的距离。

输出格式：

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点$u$到结点$v$间距离。

输入输出样例

输入样例#1：

输出样例#1：

4
4
8

思路：对于第一个子问题，就是找树上最深的点，一遍$dfs$即可实现，对于第二个子问题，就是看看相同深度的点数目的最大值是多少，对于对三个子问题，就是通过$LCA$求两点间的树上距离。

代码：

#include<cstdio>
#include<algorithm>
#define maxn 107
using namespace std;
int f[maxn][7],n,x,y,js[maxn],maxx,head[maxn],num,d[maxn],zrj;
struct node {
  int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
  e[++num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
void dfs(int u, int fa) {
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(v!=fa) {
      f[v][0]=u;
      d[v]=d[u]+1;
      maxx=max(maxx,d[v]);
      dfs(v,u);
    }
  }
}
inline int lca(int a, int b) {
  if(d[a]>d[b]) swap(a,b);
  for(int i=6;i>=0;--i) 
  if(d[a]<=d[b]-(1<<i)) b=f[b][i];
  if(a==b) return a;
  for(int i=6;i>=0;--i)
  if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
  return f[a][0];
}
int main() {
  scanf("%d",&n);
  for(int i=1,u,v;i<n;++i) {
    scanf("%d%d",&u,&v);
    ct(u,v);ct(v,u);
  }
  dfs(1,0);
  for(int i=1;i<=n;++i) js[d[i]]++;
  for(int i=1;i<=maxx;++i) zrj=max(zrj,js[i]);
  for(int j=1;j<=6;++j)
  for(int i=1;i<=n;++i)
  f[i][j]=f[f[i][j-1]][j-1];
  scanf("%d%d",&x,&y);
  printf("%d\n%d\n%d\n",maxx+1,zrj,(d[x]-d[lca(x,y)])*2-d[lca(x,y)]+d[y]);
  return 0;
}

4. 洛谷P2136 拉近距离

题目背景

我是源点，你是终点。我们之间有负权环。 ——小明

题目描述

在小明和小红的生活中，有$N$个关键的节点。有$M$个事件，记为一个三元组$（S_i，T_i，W_i）$，表示从节点$S_i$有一个事件可以转移到$T_i$，事件的效果就是使他们之间的距离减少$W_i$。

这些节点构成了一个网络，其中节点$1$和$N$是特殊的，节点$1$代表小明，节点$N$代表小红，其他代表进展的阶段。所有事件可以自由选择是否进行，但每次只能进行当前节点邻接的。请你帮他们写一个程序，计算出他们之间可能的最短距离。

输入输出格式

输入格式：

第$1$行，两个正整数$N,M$.

之后$M$行，每行$3$个空格隔开的整数$S_i，T_i，W_i$。

输出格式：

一行，一个整数表示他们之间可能的最短距离。如果这个距离可以无限缩小，输出$“Forever love”$（不含引号）。

输入输出样例

输入样例#1：

输出样例#1：

-2

说明

对于$20\%$数据，$N \leq 10,M \leq 50$。

对于$50\%$数据，$N \leq 300,M \leq 5000$。

对于全部数据，$N \leq 1000,M \leq 10000,|W_i| \leq 100$，保证从节点$1$到$N$有路径。

思路：题意就是让你在一张图上找一条从$1$号点到$n$号点的最短路径，如果这条路径可以无限缩小，那么就输出$“Forever love”$，即存在负环，所以我们可以用$spfa$判断负环，如果一个点入队列超过$n$次，那么一定存在负环，这时直接输出$“Forever love”$并退出程序，然后spfa的过程中更新$dis$数组，即$1$号点到其它点的最短距离，然后这道题还有一个坑点就是距离不一定只有$1$号点能拉近，$n$号点也能，所以我们要用两遍$spfa$，分别以$1$号点和$n$号点为起点，然后取两次$dis[end]$的最大值，其中$end$表示两次$spfa$的重点。

代码：

#include<cstdio>
#include<cctype>
#include<queue>
#include<cstring>
#include<algorithm>
#define maxn 1007
using namespace std;
int n,m,head[maxn],in[maxn],dis[maxn],num;
bool vis[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct node {
  int v,w,nxt;
}e[20007];
inline void ct(int u, int v, int w) {
  e[++num].v=v;
  e[num].w=w;
  e[num].nxt=head[u];
  head[u]=num;
}
inline void spfa(int s) {
  memset(dis,0x3f,sizeof(dis));
  queue<int>q;
  q.push(s);
  dis[s]=0,in[s]=1,vis[s]=1;
  while(!q.empty()) {
    int u=q.front();q.pop();
    vis[u]=0;
    for(int i=head[u];i;i=e[i].nxt) {
      int v=e[i].v;
      if(dis[v]>dis[u]+e[i].w) {
        dis[v]=dis[u]+e[i].w;
        if(!vis[v]) {
          q.push(v),vis[v]=1;
          in[v]++;
          if(in[v]>n) {printf("Forever love\n");exit(0);} 
        }
      }
    }
  }
}
int main() {
  n=qread(),m=qread();
  for(int i=1,u,v,w;i<=m;++i) {
    u=qread(),v=qread(),w=qread();
    ct(u,v,-w);
  }
  spfa(1);int zrj=dis[n];
  spfa(n);int cyh=dis[1];
  printf("%d\n",min(zrj,cyh));
  return 0; 
}

2018年12月19日

一. 今日完成的题目：

二.

1. 当天完成题目数：4道。

2. 未完成6个题目的原因：上午考试了，时间不足

3. 复习的知识点：LCA，负环。

4.不会题目：洛谷P3398

三：

1. 洛谷P2912 牧场散步Pasture Walking

题目描述

输入输出格式

输入输出样例

说明

2. 洛谷P2971 牛的政治Cow Politics

题目描述

输入输出格式

输入输出样例

3. 洛谷P3884 二叉树问题

题目描述

输入输出格式

输入输出样例

4. 洛谷P2136 拉近距离

题目背景

题目描述

输入输出格式

输入输出样例

说明