牛客小白月赛 42 官方题解
恭喜上百位同学 AK ! ! 你们太强辣 ! !
A 冰狱寒岚
考虑找规律,第 个位置是 ,也就是说第 个位置就又变回了 。
据此循环节是 ,首先令 。
然后考虑分类讨论:
-
当 时:直接输出 即可。
-
当 时:观察到 ,直接输出 即可。
B 光之屏障
考虑预处理出所有 内 的幂次,即:
接着考虑对于每组询问,直接枚举每个答案 是否在 范围内即可。
预处理数组 表示 ,一开始 ,以后每一项 ,递推即可。
查询时枚举 ,直接提取出 的值判断其是否满足 即可。
C 寒潭烟光
记 的 值为 , 的 值为 。
根据定义可以知道:
同理:
联立 两式:
D 金蛇狂舞
考虑 的变化,阶乘可以使其数值大幅增加,而开方不论上取整下取整,均会使其数值大幅减少(但不如阶乘明显)。
对于 ,连续 次开根才能使其到达 的位置,算上 次阶乘恰好是 步。
据此我们知道,当 的值能使其一次阶乘之后超过 我们就可以剪枝。
直接考虑 BFS(广度优先搜索),当 很大时合理剪枝即可。
E 暗灭侵蚀
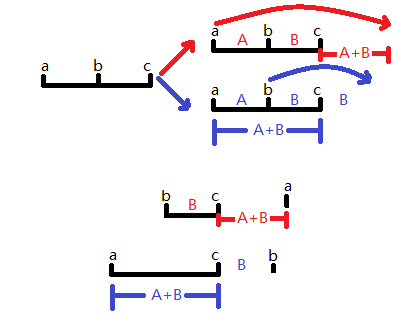
结论:每次以最左边的 向右跳即可。
证明:考虑分别设 。
一次以最左边向右的步,本质是将距离变成了
而以中间向右的步,本质上是将距离变成了
由于坐标增长的速率显然与相对距离呈正相关,所以前者的能使 坐标更靠前方式显然更优。
F 火凤燎原
sol:https://www.luogu.com.cn/paste/vg035rgp
对于一个点 ,假设 的孩子结点有 个,它们分别是 ,首先特判掉 不产生贡献的情况。
然后考虑枚举点 不作为 单点的子树,作为链的起点:
- 此时这个 对于点 的贡献,是以 为根的子树大小减一(链的长度不少于 ,所以 自己作为链的情况需要去除)。
考虑列出式子:
其中 表示以 为根的子树大小, 表示点 的度。
这个等式就是考虑容斥,把不可能作为“链”的末端的点(所有与 直接相连的点和 本身)去掉即可。
总复杂度 。
用等式左边直接做换根 dp 是内测时很受欢迎的解法,但我这个解法好写多了,不是吗?
std
A 冰狱寒岚
int main(){
int n = init();
while (n--) {
int x = init();
x %= 2048;
if (x > 1023) print(x - 2048), putchar(' ');
else print(x), putchar(' ');
}
}
B 光之屏障
int a[31];
int main(){
for (int i = 0; i < 31; ++i)
a[i] = 1 << i;
int T = init();
while (T--) {
int x = init(), y = init();
int ans = -1;
for (int i = 0; i < 31; ++i)
if (x <= a[i] && a[i] <= y)
ans = a[i];
print(ans), putchar('\n');
}
}
C 寒潭烟光
#define int long long
signed main(){
int T = init();
while (T--) {
int n = init(), Tn = init(), x1 = init();
print((n * Tn + (n + 1) * x1) / (n + 1)), putchar('\n');
}
}
D 金蛇狂舞
#define int long long
int factorial(int n){
if (n == 0) return 1;
return n * factorial(n - 1);
}
std::map<int, int>dis; std::queue<int>queue;
signed main(){
int x = init(), y = init();
dis[x] = 0; queue.push(x);
while (!queue.empty()) {
int u = queue.front(); queue.pop();
if (dis[u] >= 7 || u == y) break;
if (u <= 19) {
int v = factorial(u);
if (!dis.count(v)) dis[v] = dis[u] + 1, queue.push(v);
}
int w1 = floor(sqrt((double) u)), w2 = ceil(sqrt((double) u));
if (!dis.count(w1)) dis[w1] = dis[u] + 1, queue.push(w1);
if (!dis.count(w2)) dis[w2] = dis[u] + 1, queue.push(w2);
}
if (dis.count(y)) print(dis[y]), putchar('\n');
else print(-1), putchar('\n');
}
E 暗灭侵蚀
#define int long long
struct Node{
int a, b, c;
};
Node R(Node p){
return (Node){p.b, p.c, p.c * 2 - p.a};
}
signed main(){
int T = init();
while (T--) {
int a = init(), b = init(), c = init(), N = init();
Node p = (Node){a, b, c};
int ans = 0;
while (p.c < N) ++ans, p = R(p);
print(ans), putchar('\n');
}
}
F 火凤燎原
typedef long long ll;
int main(){
int T = init();
while (T--) {
memset(du, 0, sizeof(du));
int n = init();
for (int i = 1; i < n; ++i)
++du[init()], ++du[init()];
ll ans = 0;
for (int i = 1; i <= n; ++i)
if (du[i] >= 3)
ans += n - 1 - du[i];
print(ans), putchar('\n');
}
}
彩蛋
Problem A Problem B


Problem D Problem E
爱,是生命的扩充。
而且,是最有效、最良性的扩充。
爱上一个人,你的生命就结束了孑然一身的孤独状态,至少扩充了一倍。爱的对象有家人,有朋友,有职业,有单位,那就还会爱屋及乌,使爱意广泛弥散开来。因为相关的这一切都会让你入心,让你微笑,已经成为你生命的延伸地带。
如果你爱的人相当优秀,那事情就更大了。你从他的谈吐,亲近了冷漠历史、陌生远方;你从她的容貌,拥有了远山浅黛、秋云初雪。
更重要的是,一旦投入了这样的爱,你们就立即能与自古以来中外一切表述人间至情的作品心心相印。也就是说,你们的生命扩充到了人类最美好的领域,无边无际。
杂谈
感谢 CSP_Sept 提供 C 题的优质 idea。
D 题 idea 来源于《数学万花筒》系列,但是记不清是哪一本了。
事实上 E 题有个 “小哥哥”,但它并不是 D 题,而是这个题:https://www.luogu.com.cn/problem/U174241 。
这个结构的思路来源,是一道古典的 LCA 练习题,一些老年人都知道。
F 题 idea 来源于《八仙过海》系列树论题单,是不是很带劲?
一些个表情包




赛后评价
征集赛后评价:
- 题目描述需要改进的地方?(除广播过的内容之外,统一回复下 F 题关于“度”的定义,当时内测时经群内讨论,由于互联网上有很多关于该概念的定义,并且说法一致,并无争议,因此内测群当时即认为不需要解释,若因此为您带来不便,深感抱歉)
- 数据是否有过水的地方?(根据各题的性质,可能只有 F 题需要卡的没卡掉吧?)
- 答疑是否有需要改进的地方?(很重要)
- 题目名字和题目背景写的咋样啊?(很重要很重要)
- 其他想对出题人说的话,仅限与这场比赛的赛题或其背景有关的。
赛后第三天会在楼下以回复的形式展示本次调查的结果,为了之后的比赛做得更好,请您多多提出建议!感谢!
均为非必答题 ^_^
The Last but not least





 京公网安备 11010502036488号
京公网安备 11010502036488号