2022-08-18:每一个序列都是[a,b]的形式，a ＜ b 序列连接的方式为，前一个序列的b

2022-08-18:每一个序列都是[a,b]的形式，a < b 序列连接的方式为，前一个序列的b，要等于后一个序列的a 比如 : [3, 7]、[7, 13]、[13, 26]这三个序列就可以依次连接 给定若干个序列，求最大连接的数量 定义尝试过程如下 arr[i] = {4, 9}表示，第i个序列4开始，9结束 pre : 代表选择的上一个序列，的，index是多少 比如选择的上一个序列如果是(4,9)，是第5个序列，那么pre==5 特别注意：如果从来没有选过序列，那么pre == -1 这个函数含义 : index....所有的序列，随便选择。index之前的序列，不能选择 上一个选择的序列，是pre号，如果pre==-1,说明之前没有选择过序列 返回题目要求的那种连接方式下，最大的序列数量 [5,13] [1,19] [2, 3] [79, 81] ... [1,19] [2, 3] [5, 13] [79, 81] arr[i][0] : 开头 arr[i][1] : 结尾 arr已经根据开头排过序了！ preEnd index [1, 3] [2, 4] [4, 7] 0 1 2 maxLen(0, -1) 0（选） -> maxLen(1, 0) 在arr[index...]选择序列，之前选的，离index最近的序列，位置在preIndex 请返回，index...能链接起来的，序列数量的最大值

答案2022-08-18：

递归。要i还是不要i。 时间复杂度：O(N**2)。

代码用rust编写。代码如下：

fn main() {
    let mut arr: Vec<Vec<i32>> = vec![vec![1, 3], vec![3, 4], vec![4, 7]];
    let ans1 = max_len(&mut arr, 0, -1);
    println!("ans1 = {}", ans1);
    let ans1 = max_number_subsequence(&mut arr, 0, -1);
    println!("ans2 = {}", ans1);
}

fn max_len(arr: &mut Vec<Vec<i32>>, index: i32, pre_index: i32) -> i32 {
    if index == arr.len() as i32 {
        return 0;
    }
    // 还有序列可以选
    // index号序列
    // 不选
    let p1 = max_len(arr, index + 1, pre_index);
    // 选
    let mut p2 = 0;
    // [3,17] index(9,24)
    if pre_index == -1 || arr[pre_index as usize][1] == arr[index as usize][0] {
        // 才能选
        p2 = 1 + max_len(arr, index + 1, index);
    }
    return get_max(p1, p2);
}

// O(N^2)
fn max_number_subsequence(arr: &mut Vec<Vec<i32>>, index: i32, pre: i32) -> i32 {
    if index == arr.len() as i32 {
        return 0;
    }
    // 就是不要当前序列
    let p1 = max_number_subsequence(arr, index + 1, pre);
    // 要当前序列
    let mut p2 = -1;
    if pre == -1 || arr[pre as usize][1] == arr[index as usize][0] {
        p2 = 1 + max_number_subsequence(arr, index + 1, index);
    }
    return get_max(p1, p2);
}

fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a > b {
        a
    } else {
        b
    }
}

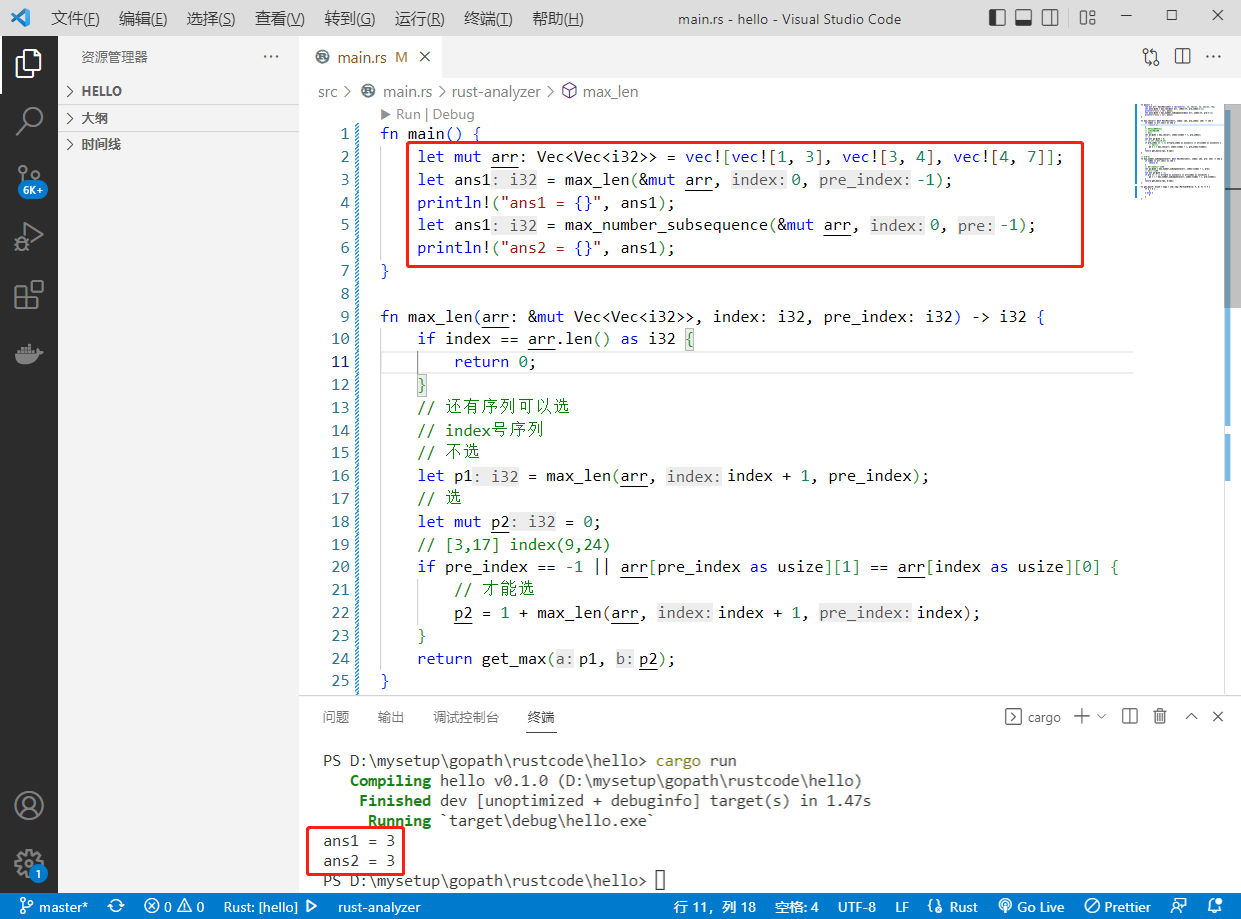
执行结果如下：

左神java代码