描述

题目描述

首先给定我们一个排列，让我们求出来他的下一个排列是多少，如果当前已经是最大的排列了，我们直接输出最小的排列就可以了

什么是排列的顺序，假设我们从1...n那么我们按照字典序的顺序，构造我们的排列，按位比较小的字典序小，并且排列更小

样例解释

样例输入'[1,2,3]'

这里我们给出我们的这个的所有可能的一个排列

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

这个就是我们的所有排列，我们很容易找到他的下一个排列是'[1,3,2]'

所以我们最后的样例输出就是'[1,3,2]'

题解

解法一：使用C++库函数

解法思路

我们可以直接使用C++内部含有的求取下一个排列的库函数，直接获取到我们所有的可能排列，然后找到我们当前的排列的下一个是什么

代码实现

class Solution {
public:
    vector<int> nextPermutation(vector<int>& nums) {
        next_permutation(nums.begin(), nums.end());
//         求取 下一个全排列
        return nums;
//         返回
    }
};

简单介绍库函数

这里简单介绍一下这个神器$nex{t}_{p}ermutationnext\_permutation$，这个是我们C++中的求取下一个排列的函数，将当前排列更改为 全排列中的下一个排列。如果当前排列已经是 全排列中的最后一个排列（元素完全从大到小排列），函数返回 false 并将排列更改为 全排列中的第一个排列（元素完全从小到大排列）；否则，函数返回 true。next_permutation(v.begin(), v.end()) 或 next_permutation(v + begin, v + end)。

时空复杂度分析

时间复杂度： $O(n)O(n)$

理由如下，我们这个库函数的平均的时间复杂度为$O(n)O(n)$

空间复杂度： $O(1)O(1)$

理由如下，我们未引入变量空间

解法二：手写库函数

实现思路；

首先我们可以想一下，除了最大的那个排列之外，我们的排列都是后面的大于前面的，那么我们就有了这样的一个思路，我们从后面开始找到第一个降序的位置，说明我们把这位改变，对整体影响最小，然后我们在从后往前找到第一个比我们刚才那个位置的值大的数字，然后我们交换二者，最后把我们刚才的那个位置后面的地方反转，因为我们交换完成之后是一个升序的序列，我们反转就可以得到降序的序列，使我们的影响最小

图解代码

我们拿这组数据举例子'[1,2,4,3]'

第一步找到降序的位置

然后记住这个位置，从后向前找到第一个比这个位置的值大的位置

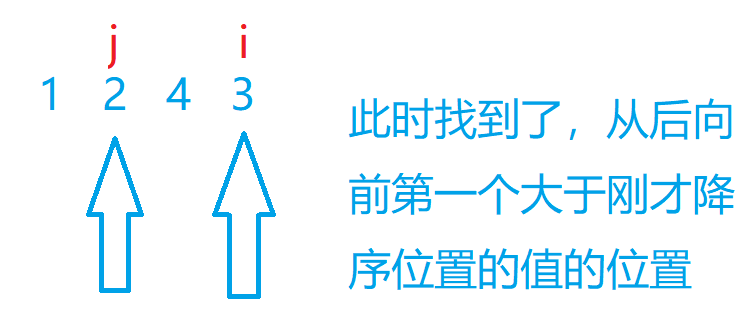
然后我们交换二者得到

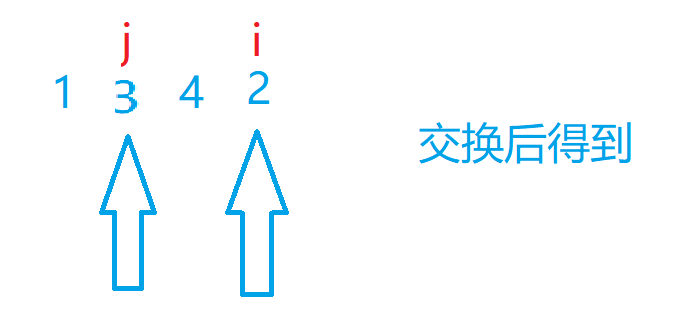
最后翻转刚才位置后面的元素

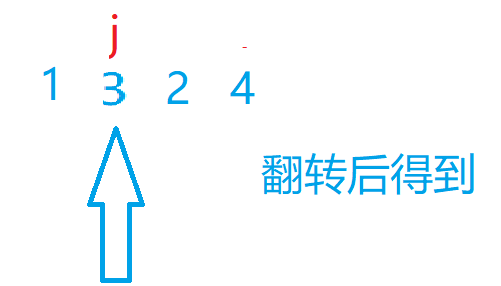
代码实现：

class Solution {
public:
    vector<int> nextPermutation(vector<int>& nums) {
        int idx = -1, n = nums.size(), val = INT_MAX, end = -1;
        for (int i = n - 2; i >= 0; i--) {
            if (nums[i] < nums[i + 1]) {
                idx = i;
                break;
            }
        }
//         这个是找到第一个降序的位置 
        if (idx != -1) {
//             如果存在降序的位置，证明不是最大的那个序列
            for (int i = n - 1; i > idx; i--) {
                if (nums[i] > nums[idx]) {
                    end = i;
                    break;
                }
            }
//             找到第一个比我们降序位置大的数字，从后往前查找
            swap(nums[end], nums[idx]);
//             交换这两个位置
        } 
        reverse(nums.begin() + idx + 1, nums.end());
//         反转降序位置后面的所有数字
        return nums;
    }
};

时空复杂度分析

时间复杂度： $O(n)O(n)$

理由如下，我们只是遍历了一遍我们的长度为$nn$的数组，并且翻转

空间复杂度： $O(1)O(1)$

理由如下，我们只引入了常数级空间