描述
题目描述
首先给我们一颗二叉树, 然后让我们去遍历这颗二叉树, 问我们是不是可以找到一条路径可以满足, 这条路径上面的节点的总和等于我们的目标值, 并且我们的这个节点的最后的末尾要是叶子节点, 叶子节点的定义就是左右孩子都是空指针
题解
解法一:
实现思路
我们可以使用枚举每一条从根节点到叶子节点的距离, 然后我们遍历到我们的叶子节点, 如果我们的路径和恰好为目标和的时候, 我们就是找到了一条满足条件的路径了
代码实现
class Solution {
bool flag = false;
// 用于判断我们最后是否可以找到一条路径可以满足条件的
public:
void dfs(TreeNode *root, int tar) {
if (flag) return;
// 如果找到了答案直接返回就可以了
if (root == nullptr) return;
// 如果当前的节点是空指针, 那么我们可以直接返回
tar -= root->val;
// 我们的目标值减去当前的这个节点的值
if (root->left == nullptr && root->right == nullptr && tar == 0) {
flag = true;
// 如果是叶子节点, 并且我们的目标值等于0了, 代表我们找到了
}
dfs(root->left, tar);
dfs(root->right, tar);
// 分别递归判断左右子树
}
bool hasPathSum(TreeNode *root, int sum) {
dfs(root, sum);
// 遍历我们的这颗树
return flag;
}
};
时空复杂度分析:
时间复杂度:
理由如下: 我们最坏的情况就是把整颗树遍历了一次, 那么我们的时间复杂度就是遍历了所有的节点, 那么时间复杂度就是的
空间复杂度:
理由如下: 极限情况下, 就是一条链, 我们的空间就是系统递归栈的深度, 就是
解法二: BFS
实现思路
其实我们的思路和我们的差不多, 也是把整个一颗树遍历一次, 到了最后的节点的时候, 我们考虑是否可以使得路径上的值恰好等于我们的要求的这个目标值, 那么我们如何实现呢? 我们可以用两个队列, 一个是存储我们要遍历的节点, 一个是存储根节点到这些节点的路径和是多少
图解代码
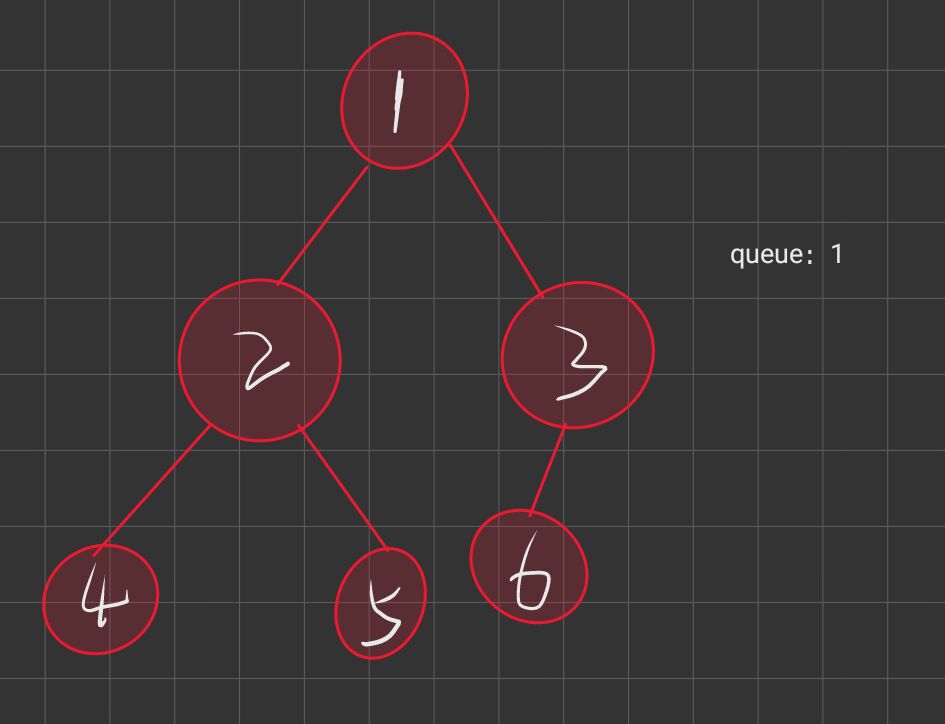
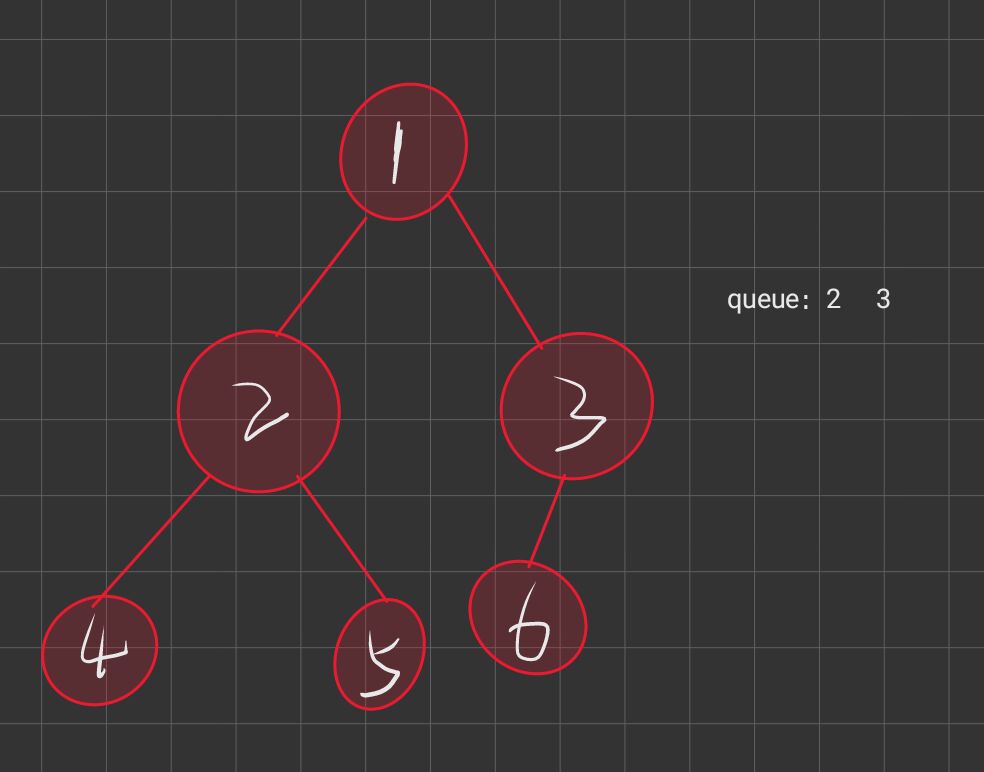
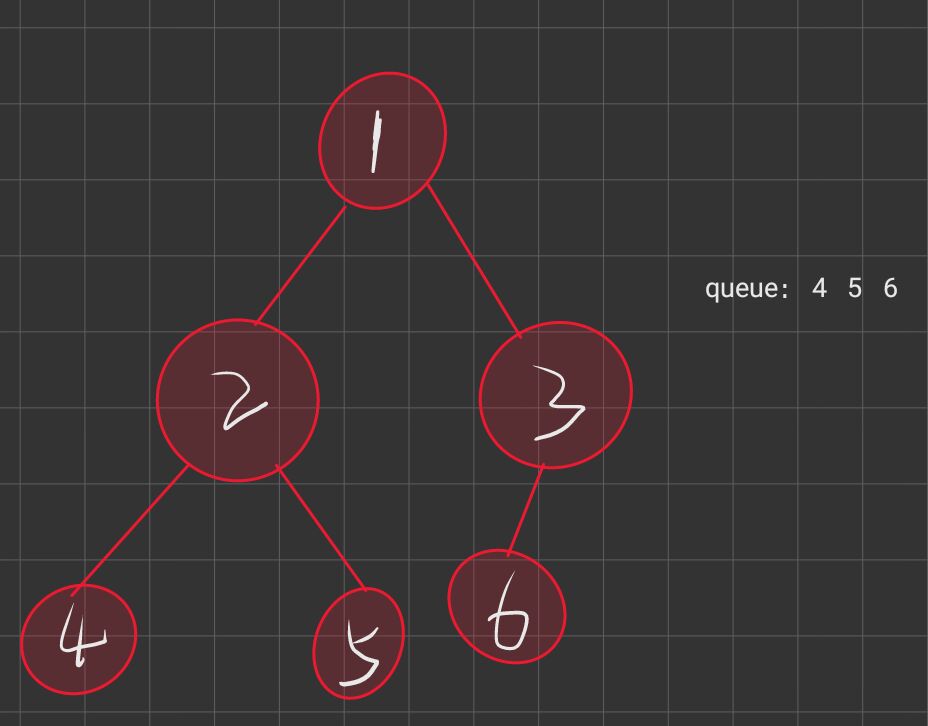
代码实现
class Solution {
public:
bool hasPathSum(TreeNode *root, int sum) {
if (root == nullptr) return false;
// 如果是空节点返回false
queue<TreeNode*> q;
// q是我们存我们所有树上点的队列
queue<int> val;
// 这个是存储我们路径的值
q.emplace(root);
val.emplace(root->val);
// 初始放入
while (!q.empty()) {
auto tmp = q.front();
int tmp_val = val.front();
// 取出队头
q.pop();
val.pop();
if (tmp->left == nullptr && tmp->right == nullptr) {
if (tmp_val == sum) return true;
// 找到了
continue;
}
if (tmp->left != nullptr) {
q.emplace(tmp->left);
val.emplace(tmp->left->val + tmp_val);
}
if (tmp->right != nullptr) {
q.emplace(tmp->right);
val.emplace(tmp->right->val + tmp_val);
}
// 分别判断左右子树是否到了叶子节点
}
return false;
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们需要把所有的节点遍历一次, 所以我们的时间复杂度是的
空间复杂度:
理由如下: 我们存储了我们的树的节点数, 队列中最多可能会有一半的节点, 所以我们的空间复杂度是的






 京公网安备 11010502036488号
京公网安备 11010502036488号