描述

题目描述

首先我们有一个二叉树, 要求我们把我们的每一层的一个值都存储下来, 然后我们直接存到了一个二维数组里面, 然后我们遍历的时候再直接返回就可以了

题解

解法一: 暴力DFS

实现思路

我们可以直接首先暴力$dfsdfs$一次, 获取到我们最后的最高的树高, 然后我们开辟我们的答案的数组存储我们的这个树的节点, 然后我们直接再一次遍历的时候我们可以直接去把值存到我们的这个二维数组里面, 然后我们直接返回即可

代码实现

class Solution {
    int maxx = 0;
    // 这个maxx是我们的一个最大的深度
   public:
    void getHeight(TreeNode *root, int h) {
        maxx = max(maxx, h);
        // 每次寻找我们的最大的深度
        if (root == nullptr) return;
        // 如果是空节点返回
        if (root->left != nullptr) getHeight(root->left, h + 1);
        // 遍历我们的左子树
        if (root->right != nullptr) getHeight(root->right, h + 1);
        // 遍历我们的右子树
    }
    void dfs(TreeNode *root, int h, vector<vector<int>> &res) {
        res[h].emplace_back(root->val);
        // 把我们对应层塞入相应的值
        if (root->left != nullptr) dfs(root->left, h + 1, res);
        // 遍历我们的左子树
        if (root->right != nullptr) dfs(root->right, h + 1, res);
        // 遍历我们的右子树
    }
    vector<vector<int>> Print(TreeNode *pRoot) {
        if (pRoot == nullptr) return vector<vector<int>>();
        // 如果是空的，我们直接返回
        getHeight(pRoot, 0);
        // 我们获取最大的深度
        vector<vector<int>> res(maxx + 1);
        // 我们最后的答案
        dfs(pRoot, 0, res);
        // dfs存储我们的答案结果
        return res;
    }
};

时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 因为我们需要把我们的所有节点都要遍历一次, 所以我们的时间复杂度就是$O(n)O(n)$的

空间复杂度: $O(n)O(n)$

理由如下: 首先我们的结果数组不计入最后的空间, 然后我们递归的过程中, 最为极限的情况下就是退化成为一条链, 那么我们就是系统的递归栈的深度就是$nn$, 所以我们的空间复杂度就是$O(n)O(n)$

解法二: BFS

实现思路

我们可以开辟一个队列, 然后我们每一次只需要把当前这层的元素都放入我们的这个队列里面, 然后我们把这个队列里面的东西都给放到我们的答案数组里面, 然后我们不断这样迭代, 然后我们用$bfsbfs$遍历之后, 我们就可以得到我们最后的答案数组了

图解代码

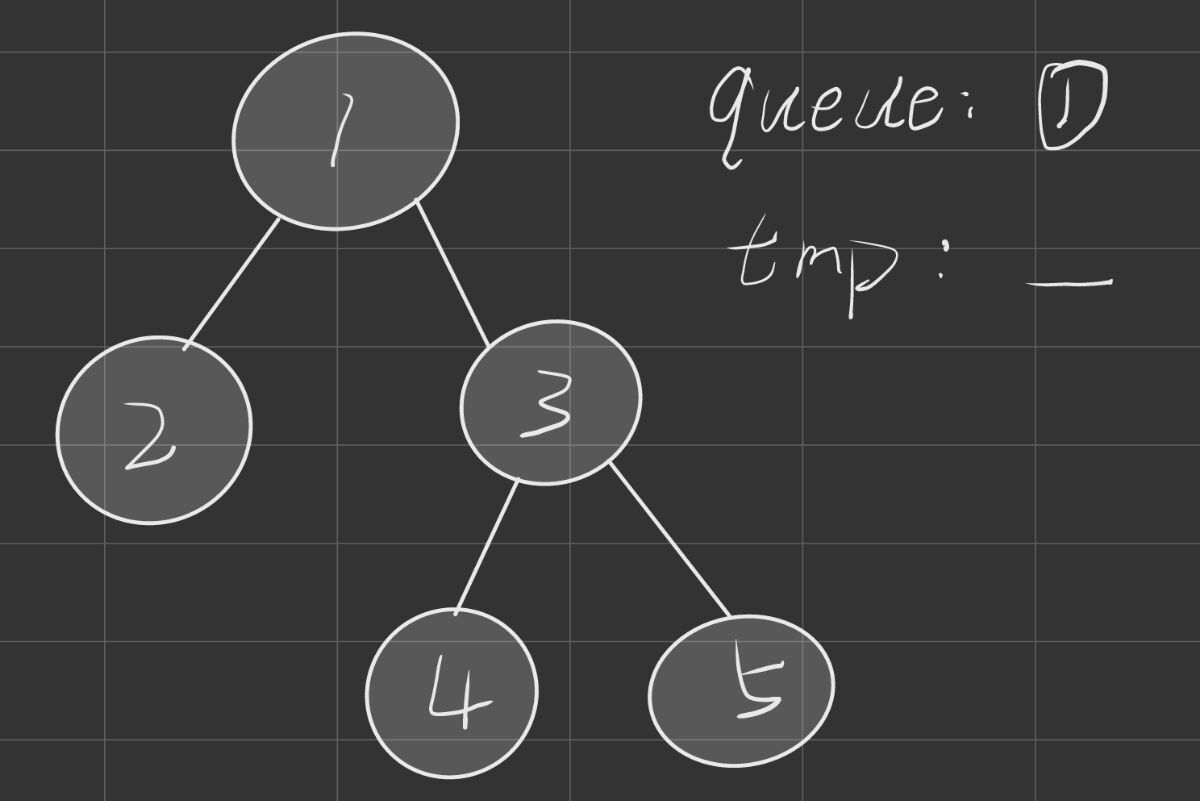
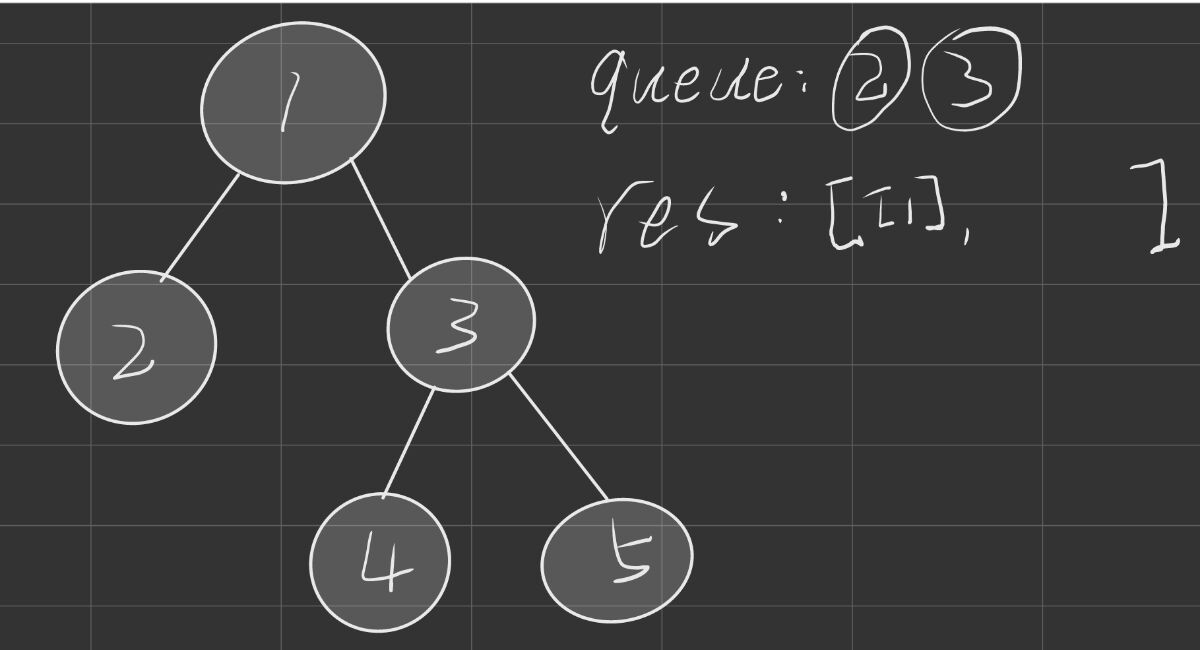
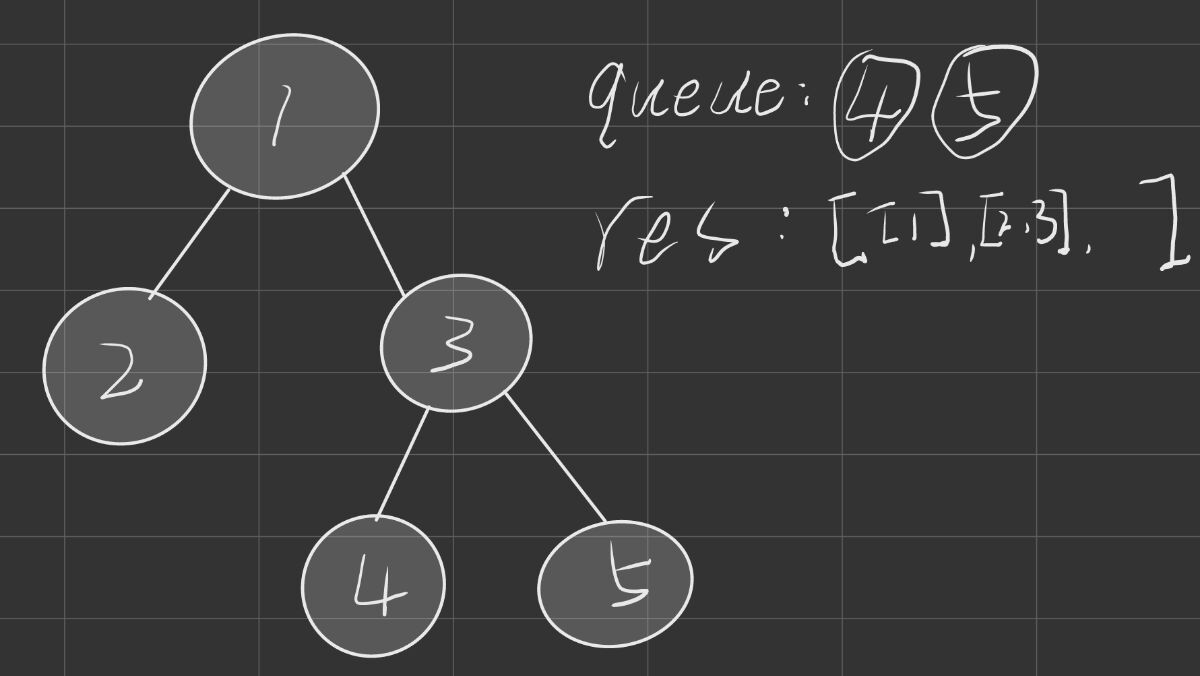
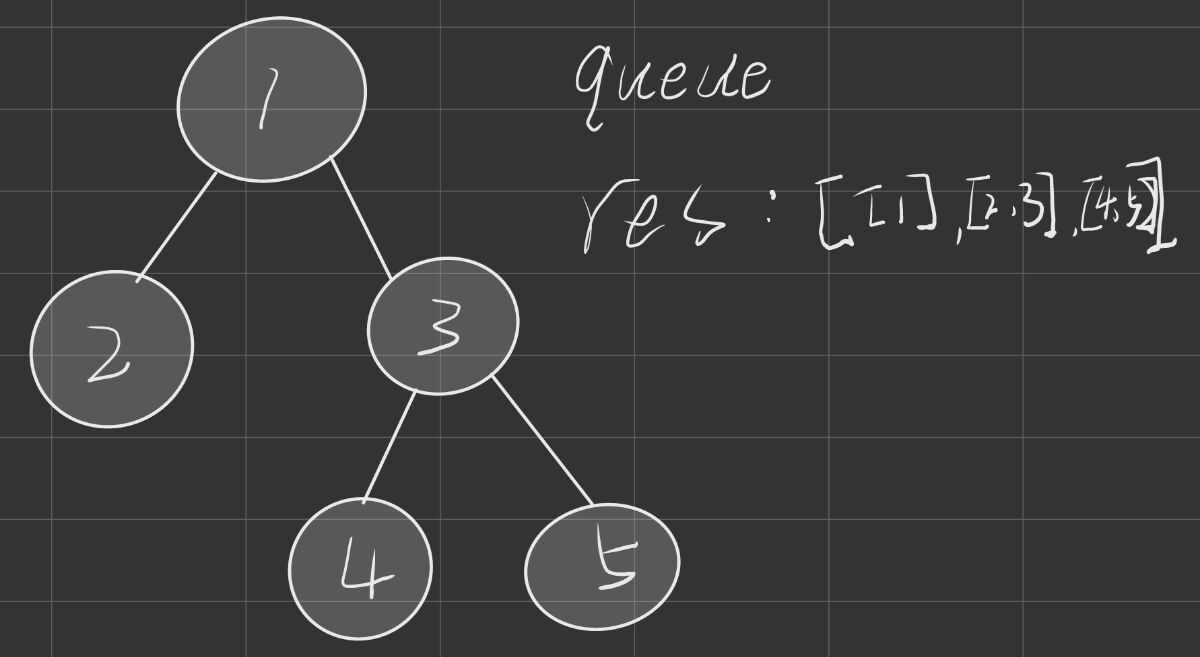
代码实现

class Solution {
   public:
    vector<vector<int>> Print(TreeNode *pRoot) {
        vector<vector<int>> res;
        // 我们最后的答案数组
        if (pRoot == nullptr) return res;
        // 如果我们当前的这个是空节点, 那么我们直接返回我们原来的空数组
        queue<TreeNode *> q;
        // 这个队列用于存储我们每一层的节点
        q.push(pRoot);
        // 首先把我们的根节点放入我们的队列之中
        while (!q.empty()) {
            // 当我们的队列不为空的时候
            vector<int> tmp;
            // 我们的临时数组
            int n = q.size();
            for (int i = 1; i <= n; i++) {
                auto node = q.front();
                tmp.emplace_back(node->val);
                q.pop();
                // 把我们当前的这层的值放入临时数组
                if (node->left != nullptr) q.push(node->left);
                if (node->right != nullptr) q.push(node->right);
                // 把我们的左右孩子放入队列，供我们下一次的使用
            }
            res.emplace_back(tmp);
            // 把我们的临时数组放到我们的这个答案数组之中
        }
        return res;
    }
};

时空复杂度分析:

时间复杂度: $O(n)O(n)$

理由如下: 因为我们的这个$bfsbfs$需要遍历我们的所有的节点, 所以我们的时间复杂度是$O(n)O(n)$的

空间复杂度: $O(n)O(n)$

理由如下: 因为我们最坏的情况下, 我们会有一半的节点在我们的队列里面, 所以我们的空间的级别还是$O(n)O(n)$的