题目

题目链接

Median

题意

3个数产生一个中位数，现在给你一串中位数，请还原出一个合理的原串

Input

T组,每组给n表示原串的长度,然后是给你中位数串b[1]->b[n-1]

范围: n的和不超过10^6,每个b不超过10^9

Output

有合理的串则输出原串,否则输出-1

题解

结论

若存在合理的解,那么解的每个位置的最终值一定是它能影响到的3个中位数之一

证明

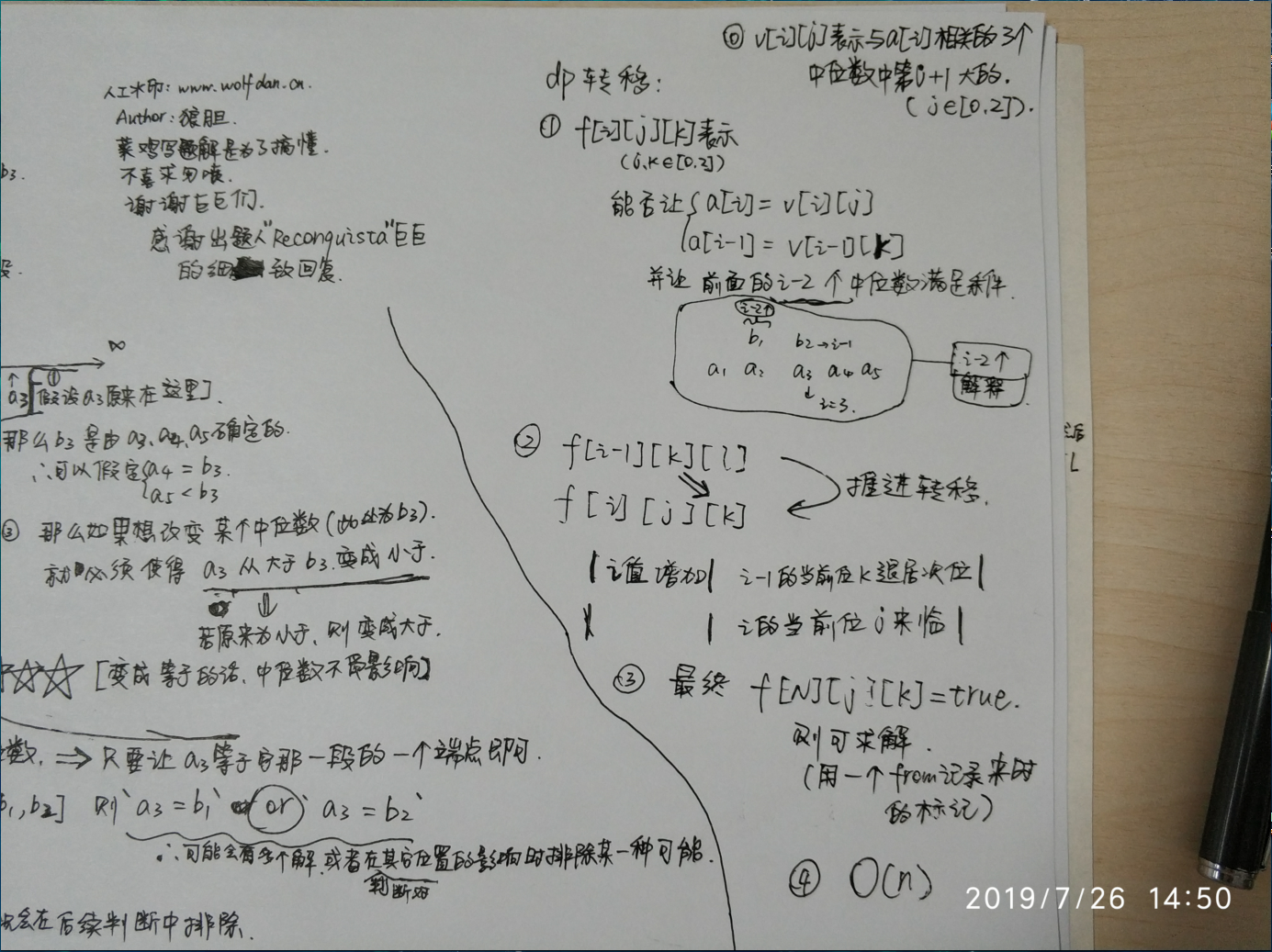
Dp解法

自己动手写AC代码

#include<bits/stdc++.h>
using namespace std;
const int M = 1e5+7;

bool f[M][3][3];
int pre[M][3][3];
int v[M][3];
int b[M],a[M];
int T,n;

int mid(int x,int y,int z){
    static int tmp[3];
    tmp[0]=x,tmp[1]=y,tmp[2]=z;
    sort(tmp,tmp+3);
    return tmp[1];
}

/*回溯构造*/
void back(int i,int j,int k){
    while(i>=1) {
        a[i] = v[i][j];
        int pr = pre[i][j][k];
        j = k;
        k = pr;
        i--;
    }
}

int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        for(int i=2;i<=n-1;i++) scanf("%d",&b[i]);
        /*init*/
        b[0]=b[1]=b[2]; b[n+1]=b[n]=b[n-1];
        for(int i=1;i<=n;i++)
            for(int j=0;j<3;j++)
                for(int k=0;k<3;k++)
                    f[i][j][k]=false;
        /*注意:我给的手写题解中a[3]对应b[1],b[2],b[3]
         我这里为了实现方便是用的对应b[2],b[3],b[4]*/
        for(int i=1;i<=n;i++){
            for(int j=0;j<3;j++){
                v[i][j]=b[i-1+j];
            }
            sort(v[i],v[i]+3);
        }
        /*边界条件: 前i-2个中位数(此时i=2为0个中位数)是满足条件的
          最终f[N][i][j]的时候的是N-2个中位数是否满足条件*/
        for(int i=0;i<3;i++)
            for(int j=0;j<3;j++)
                f[2][i][j]=true;

        /*solve*/
        bool findans = false;
        for(int i=3;i<=n;i++){
            for(int j=0;j<3;j++){
                for(int k=0;k<3;k++){
                    for(int l=0;l<3;l++){
                        if(!f[i-1][k][l]) continue;
                        /*判断前面的位置和本位置使用与他们位置相关的
                        3个中位数的排列中哪些排列能够满足要求
                        v[i][j]对应的是b[i-1],b[i],b[i+1]中的一个*/
                        if(mid(v[i-2][l],v[i-1][k],v[i][j])!=b[i-1])
                            continue;
                        f[i][j][k]=true;
                        /*记录下前面使用的是l大的*/
                        pre[i][j][k]=l;
                        /*break写完再探索-std中用了break
                        我认为应该遍历全部情况,所以去掉了break
                        然后两份代码都AC了,所以可能解唯一或者是按照std
                        生成的数据吧*/
                        // break;
                    }
                    if(i==n && f[i][j][k]){
                        findans = true;
                        back(i,j,k);
                        goto END;
                    }
                }
            }
        }
        END:
        if(!findans)
            printf("%d\n",-1);
        else{
            for(int i=2;i<n;i++) {
                assert(mid(a[i-1],a[i],a[i+1]) == b[i]);
            }
            for(int i=1;i<=n;i++){
                printf("%d%c",a[i]," \n"[i==n]);
            }
        }

    }

    return 0;
}