Genshin Impact's Fault
题意
给定连续多次的原神许愿池祈愿结果(有三星,四星,五星,Up 五星),考虑大小保底以及每两个五星必出 Up 五星的规则(原神抽卡真的是按照这个规则吗),判断祈愿结果是否合法。
分析
依照题意模拟即可。
代码
#include<bits/stdc++.h>
const int N=11e5;
#define up(a,b,c) for(int a=b;a<=c;++a)
using namespace std;
int T,n,sm[N];
bool ok;
string s;
int main()
{
cin>>T;
while(T--)
{
cin>>s,n=s.size(),ok=1,s='.'+s;
up(i,1,n)sm[i]=sm[i-1]+(s[i]!='3');
up(i,10,n)if(sm[i]==sm[i-10])ok=0;
up(i,1,n)sm[i]=sm[i-1]+(s[i]=='5'||s[i]=='U');
up(i,90,n)if(sm[i]==sm[i-90])ok=0;
bool la=1;
up(i,1,n)
{
if(s[i]=='5')
{
if(!la)ok=0;
la=0;
}
if(s[i]=='U')la=1;
}
puts(ok?"valid":"invalid");
}
return 0;
}
Cake
题意
Alice 和 Bob 玩游戏,一棵有根树每条边标有 ,一个小人从根向下走到叶子,Alice 决定奇数层的走法,Bob 决定偶数层的走法,最终顺次得到一个
串 Bob 可以任选一个前缀, Alice 希望最大化
的占比,而 Bob 希望最小化它,问最终
的占比。
分析
经典 minimax 博弈,决策树就是这棵树,模拟即可,。
代码
#include<bits/stdc++.h>
const int N=11e5;
#define up(a,b,c) for(int a=b;a<=c;++a)
using namespace std;
int T,n;
double f[N];
struct edge
{
int v,w;
};
vector<edge>to[N];
void dfs(int u,int la,int sm,int dp)
{
if(to[u].size()==1&&to[u][0].v==la)
f[u]=1.0*sm/dp;
else
{
if(dp&1)f[u]=1.0;
else f[u]=0.0;
for(edge z:to[u])
if(z.v!=la)
{
dfs(z.v,u,sm+z.w,dp+1);
if(dp&1)f[u]=min(f[u],f[z.v]);
else f[u]=max(f[u],f[z.v]);
}
if(dp)f[u]=min(f[u],1.0*sm/dp);
}
}
int main()
{
cin>>T;
while(T--)
{
cin>>n;
up(i,1,n)to[i].clear();
up(i,1,n-1)
{
int u,v,w;
cin>>u>>v>>w;
to[u].push_back({v,w}),
to[v].push_back({u,w});
}
dfs(1,0,0,0);
printf("%.12lf\n",f[1]);
}
return 0;
}
Cake 3
题意
构造 个点(或确认无解),使得所有点对中最近的点对中,这
个点每个有
次被计入,
。
分析
题意隐含的信息是点对个数为 ,故
必须至少有一个偶数,不符合的直接无解。
发现 的情况,取凸包上的一个点,以及与它对应的
个点至少有两对离得更近(因为最小夹角小于六十度),所以不可能,可以直接输出无解。
,显然对于
是偶数都有解,方法就是两两配对,然后不同对之间隔得远远的。
,单位元的
等分点搞定。
,最狗屎的部分。
首先
肯定不行,
你发现一定是个空间立方体……
难道无解?不可能,我们猜测会形成一堆等边形状,所以拿等边三角形试一试可以尝试出这货:
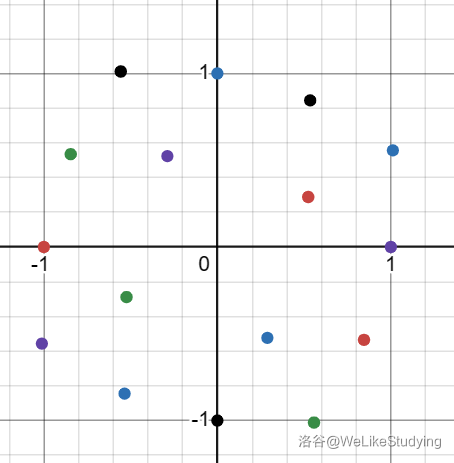 故
故 被四整除的情况有解了(
时)。
的情况也类似,往里面塞进去一个正方形就是了,如图:
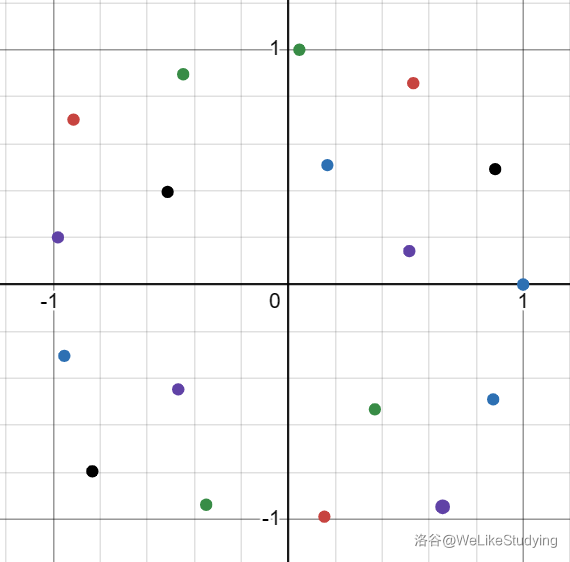 当
当 的时候,这两种构造方

然后你要解一个和三角函数有关的方程,让二分来帮助你吧!注意多元方程要二分里面再嵌套二分哟!
代码
#include<bits/stdc++.h>
#define up(a,b,c) for(int a=b;a<=c;++a)
const double Pi=acos(-1),G3=sqrt(3);
using namespace std;
int n,k;
double X,Y;
void opt(double p,double r=1,double xx=0,double yy=0)
{
printf("(%.12lf,%.12lf)\n",X=xx+cos(p)*r,Y=yy+sin(p)*r);
}
int main()
{
cin>>n>>k;
if(((n*k)&1)||k==3&&n<12||k>=4)puts("NO");
else
{
puts("YES");
if(k==1)up(i,1,n/2)up(z,0,1)opt(4*Pi*(3*i+z)/3/n);
else if(k==2)up(i,1,n)opt(2*Pi*i/n);
else if(!(n&3))
{
double s=4*Pi/n,l=0,r=4*Pi/n,md;
up(i,1,33)
{
md=(l+r)/2;
if(sin(md)/sin(s-md)<G3)l=md;
else r=md;
}
double a=md,x=sin(s-a)*2,xx,yy,ag;
up(i,1,n/4)
opt(2*s*i),xx=X,yy=Y,opt(2*s*i+2*a),
ag=atan2(Y-yy,X-xx),
opt(ag+Pi/6,x,xx,yy),opt(ag-Pi/6,x,xx,yy);
}
else
{
int b=n/4-1,c=n/4;
double l1=0,r1=8*Pi/n,m1,l2,r2,m2,m3;
up(i,0,33)
{
m1=(l1+r1)/2,l2=0,r2=4*Pi/n;
up(j,1,33)
{
m2=(l2+r2)/2,m3=(Pi-m1-m2*b)/c;
if(sin(m2)/sin(m3)<G3)l2=m2;
else r2=m2;
}
if(sin(m1)/sin(m3)<G3+1)l1=m1;
else r1=m1;
}
double g1=m1,g2=m2,g3=(Pi-g1-g2*b)/c,x=sin(g3)*2,xx,yy,ag;
opt(0),xx=X,yy=Y,opt(g1*2),ag=atan2(Y-yy,X-xx);
opt(ag+Pi/6,x,xx,yy),opt(ag-Pi/6,x,xx,yy);
opt(ag,x,X,Y),opt(ag+Pi/2,x,X,Y);
up(i,0,n/4-2)
opt(2*((g2+g3)*i+g1+g3)),xx=X,yy=Y,opt(2*((g2+g3)*i+g1+g3+g2)),
ag=atan2(Y-yy,X-xx),
opt(ag+Pi/6,x,xx,yy),opt(ag-Pi/6,x,xx,yy);
}
}
return 0;
}
易错点
多个二分不要同时二分,要在里面嵌套,因为左右端点在下一次二分的时候可能不再适用。
Stone Merging
题意
有 堆石子,编号为
到
可重复,有
个机器编号为
到
,编号
的机器可以合并
堆石子,但如果里面有编号
的石子,那么机器会坏掉并会把其中所有编号
的石子提取出来单独分成一堆(其它放在另一堆),构造全合成一堆的方案。
分析
如果 到
中所有石子都出现过,那么最后一步就没法干。
否则考虑最后一步用到的机器为 ,首先
。
然后你发现只要 就可以只用
机器。
否则你想,要是编号有 (因为编号必须大于等于
)的机器就好了!发现
,故不是
的和是
的石子数多的那堆必定不小于
,即不小于
,所以这种情况一定可以构造。
代码
#include<bits/stdc++.h>
const int N=11e4;
#define up(a,b,c) for(int a=b;a<=c;++a)
using namespace std;
int T,n,k,a[N],b[N],x,y;
bool p[N],ok;
int main()
{
cin>>T;
while(T--)
{
cin>>n>>k,fill(p,p+n+1,0);
up(i,1,n)cin>>a[i],p[a[i]]=1;
x=find(p+2,p+k+1,0)-p;
if(x>k&&!(n==2&&k==2&&a[1]==2&&a[2]==2))puts("-1");
else
{
fill(p,p+n+1,0);
cout<<((n-1)%(x-1)!=0)+(n-1)/(x-1)<<'\n';
int j=1,t=n;y=(n-1)%(x-1)+1;
iota(b,b+n+1,0);
if(y>=2)
{
cout<<y<<' ';
bool e=count(a+1,a+n+1,y)>=y;
up(i,1,y)
{
while(((a[j]==y)^e))++j;
cout<<j<<' ';
if(i<y)p[j]=1,++j;
else b[j]=t+2-e,t+=2;
}
puts("");
}
j=1;
up(i,1,(n-1)/(x-1))
{
cout<<x<<' ';
up(i,1,x)
{
while(p[j])++j;
cout<<b[j]<<' ';
if(i<x)p[j]=1,++j;
else b[j]=t+=2;
}
puts("");
}
}
}
return 0;
}
易错点
记得讨论清楚边界情况,看到我那一堆特判就知道了,除此之外就是代码块的意义要想清楚。




 京公网安备 11010502036488号
京公网安备 11010502036488号