题目描述

首先给定了我们一个矩阵的个数n，然后接下来就是给我们n个矩阵，对于我们的每一个矩阵会给我们一个行数和列数，然后我们再给我们一个矩阵的运算法则，我们就是可以进行计算，我们对于矩阵的计算是这样解释的

我们矩阵的运算次数等于我们$a\ast b==a\mathrm{.}x\ast a\mathrm{.}y\ast b\mathrm{.}xa\; *\; b\; ==\; a.x\; *\; a.y\; *\; b.x$，然后我们的新的矩阵的行和列分别就是$a\mathrm{.}xa.x$和$b\mathrm{.}yb.y$，然后要记住的就是我们的矩阵是没有交换律的

题解

解法一：栈

实现思路

我们可以考虑这么一个问题，我们先把我们的矩阵存储下来，然后我们可以每次遇到左括号什么也不考虑，如果我们遇到了右括号我们就把栈里面的两个矩阵出栈，我们对这两个矩阵计算一下计算的次数，然后我们再构建出来我们的新的矩阵，放入我们的栈中，以此类推我们最后就可以得到我们的结果

图解代码

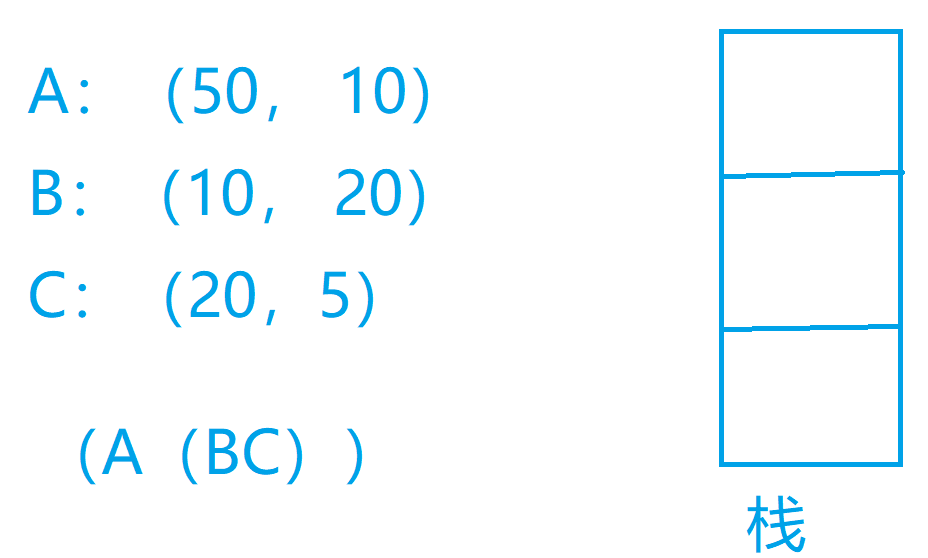
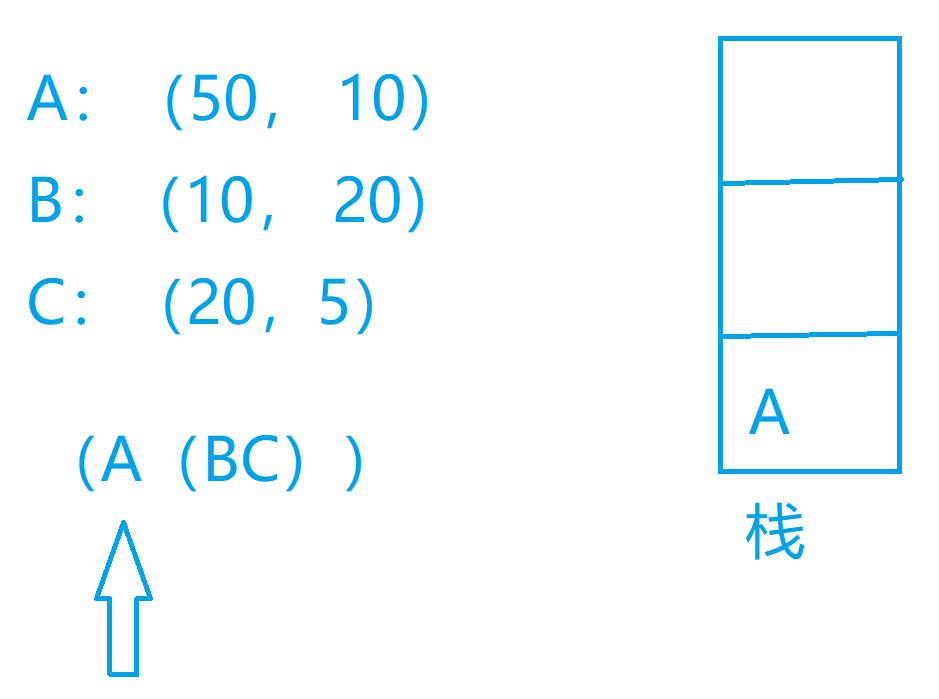
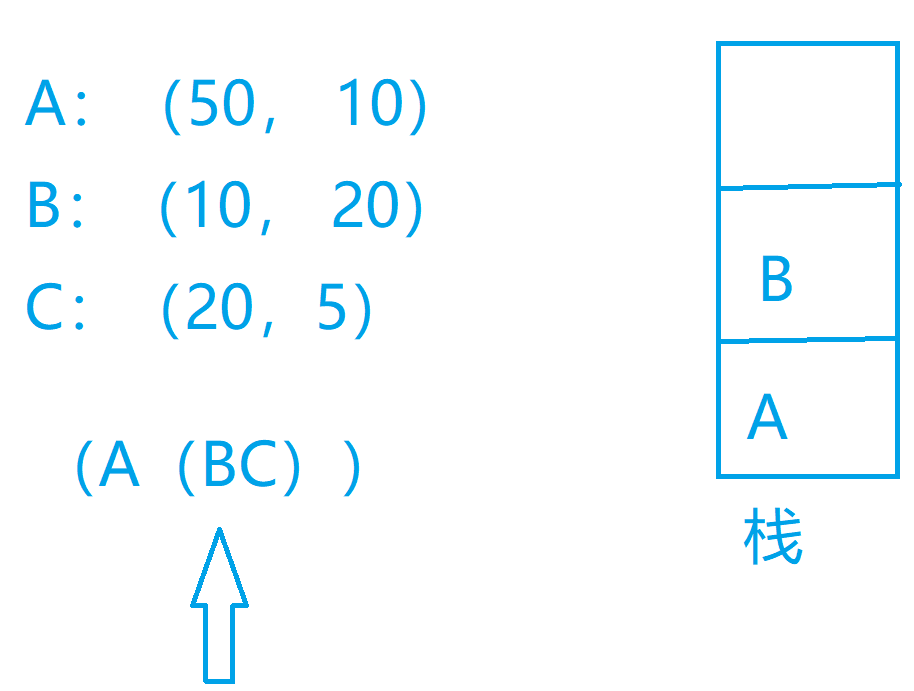
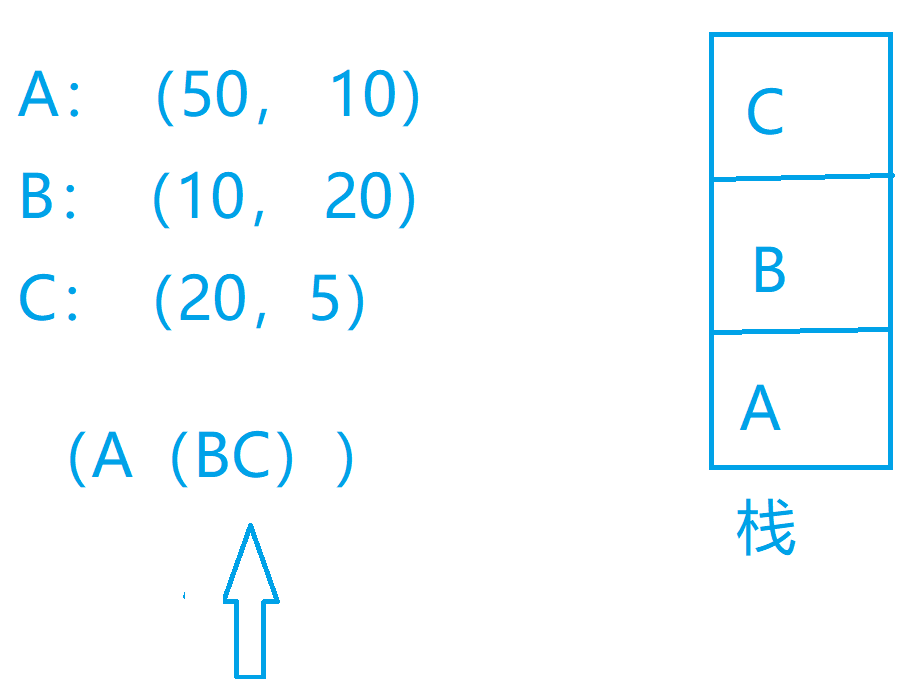
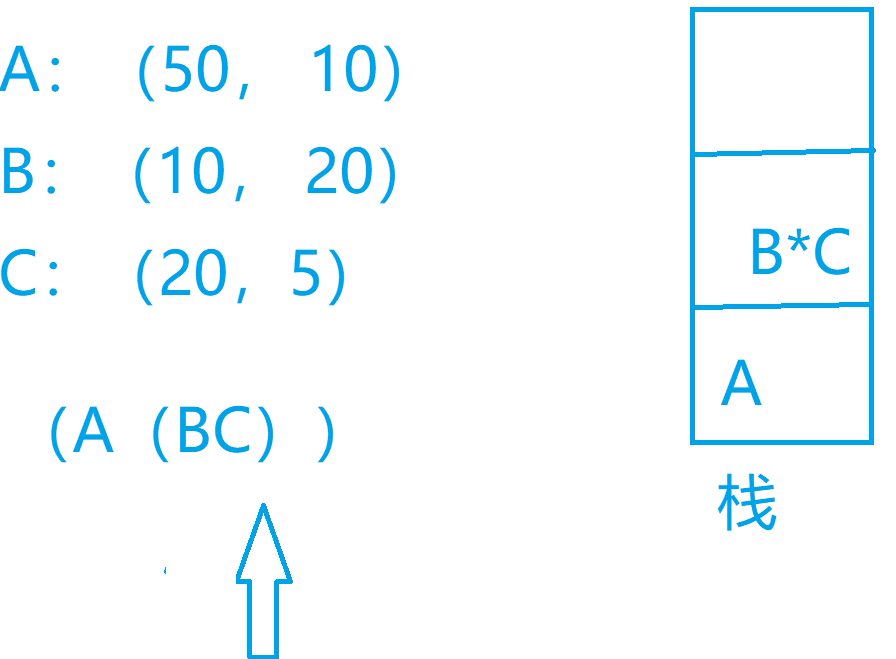
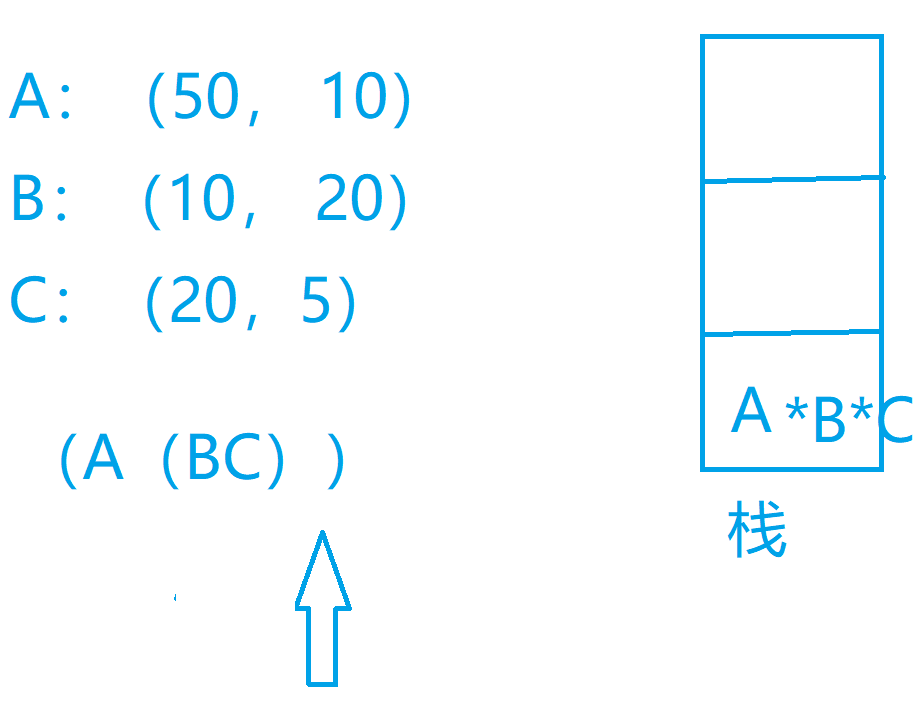
代码实现

#include <bits/stdc++.h>

using namespace std;

signed main() {
    int n;
    cin >> n;
    vector<pair<int, int>> martix(n);
    // 这个是存储我们的矩阵的开始顺序
    for (auto &[u, v] : martix) cin >> u >> v;
    // 这个是输入我们的n个矩阵
    string str;
    cin >> str;
    // 这个是我们的一个运算的法则
    reverse(martix.begin(), martix.end());
    // 我们为了让我们后续方便操作
    stack<pair<int, int>> st;
    int res = 0;
    // 我们的运算次数
    for (auto &it : str) {
        if (it == '(')
            continue;
        else if (it == ')') {
            // 如果我们当前是右括号，我们出栈两个矩阵运算
            if (st.size() <= 1) break;
            auto b = st.top();
            st.pop();
            auto a = st.top();
            st.pop();
            // 弹出两个矩阵，然后我们得到一个新的矩阵放入我们的栈种
            auto c = make_pair(a.first, b.second);
            st.emplace(c);
            // 并且计算当前的值是多少
            res += a.first * a.second * b.second;
        } else {
            // 对于我们其他的次序到了矩阵的时候，我们要入栈
            st.emplace(martix.back());
            martix.pop_back();
        }
    }
    cout << res << "\n";
    return 0;
}

时空复杂度分析

时间复杂度： $O(n)O(n)$

理由如下：事实上我们就是遍历了一次我们的整个运算的规则而已

空间复杂度： $O(n)O(n)$

理由如下：我们事实上只需要考虑这样一个问题，最坏情况下我们的栈里面要保存下来我们所有的矩阵，所以我们的空间复杂度是$O(n)O(n)$的

解法二：矩阵类

实现思路

事实上，我们可以发现这么一件事情，我们需要抽象出来这样的一个矩阵的类，我们用于干嘛呢，我们需要用这个矩阵的类来实现我们的乘法操作，这样让我们返回一个我们新的构建出来的一个矩阵，然后我们定义一个方法来实现我们计算的次数，这样有了C++的类的思想，面向对象的思路变成

代码实现

#include <bits/stdc++.h>

using namespace std;

class Martix {
   protected:
    int x, y;

   public:
    Martix() {}
    Martix(int x_, int y_) : x(x_), y(y_) {}
    int getX() { return this->x; }
    int getY() { return this->y; }
    void setX(int x) { this->x = x; }
    void setY(int y) { this->y = y; }
    int getCount(const Martix &wb) { return this->x * this->y * wb.y; }
    friend Martix operator*(const Martix &wa, const Martix &wb);
};

Martix operator*(const Martix &wa, const Martix &wb) {
    Martix martix(wa.x, wb.y);
    return martix;
}

signed main() {
    int n;
    cin >> n;
    vector<Martix> martix(n);
    for (int i = 0; i < n; i++) {
        int x, y;
        cin >> x >> y;
        martix[i].setX(x), martix[i].setY(y);
    }
    reverse(martix.begin(), martix.end());
    // 这个是构建我们的矩阵数组，并且把我们的数组放入元素
    string str;
    cin >> str;
    // 我们的运算规则
    stack<Martix> st;
    int res = 0;
    // 我们的运算次数
    for (auto &it : str) {
        if (it == '(')
            continue;
        else if (it == ')') {
            // 如果我们当前是右括号，我们出栈两个矩阵运算
            if (st.size() <= 1) break;
            auto b = st.top();
            st.pop();
            auto a = st.top();
            st.pop();
            // 弹出两个矩阵，然后我们得到一个新的矩阵放入我们的栈种
            auto c = a * b;
            st.push(c);
            // 并且计算当前的值是多少
            res += a.getCount(b);
        } else {
            // 对于我们其他的次序到了矩阵的时候，我们要入栈
            st.push(martix.back());
            martix.pop_back();
        }
    }
    cout << res << "\n";
    return 0;
}

时空复杂度分析

时间复杂度： $O(n)O(n)$

理由如下：事实上我们就是遍历了一次我们的整个运算的规则而已

空间复杂度： $O(n)O(n)$

理由如下：我们事实上只需要考虑这样一个问题，最坏情况下我们的栈里面要保存下来我们所有的矩阵，所以我们的空间复杂度是$O(n)O(n)$的