Description:

公元 2044 2044 2044 年，人类进入了宇宙纪元。

L 国有 n n n 个星球，还有 n − 1 n-1 n−1 条双向航道，每条航道建立在两个星球之间，这 n − 1 n-1 n−1 条航道连通了 L L L 国的所有星球。

小 P 掌管一家物流公司， 该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 u i u_i ui​ 号星球沿最快的宇航路径飞行到 v i v_i vi​ 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 j j j，任意飞船驶过它所花费的时间为 t j t_j tj​，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新， L L L 国国王同意小 P P P 的物流公司参与 L L L 国的航道建设，即允许小 P P P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m m m 个运输计划。在虫洞建设完成后，这 m m m 个运输计划会同时开始，所有飞船一起出发。当这 m m m 个运输计划都完成时，小 P P P 的物流公司的阶段性工作就完成了。

如果小 P P P 可以自由选择将哪一条航道改造成虫洞， 试求出小 P P P 的物流公司完成阶段性工作所需要的最短时间是多少？

Input:

第一行包括两个正整数 n , m n, m n,m，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 1 1 1 到 n n n 编号。

接下来 n − 1 n-1 n−1 行描述航道的建设情况，其中第 i i i 行包含三个整数 a i , b i a_i, b_i ai​,bi​ 和 t i t_i ti​，表示第 i i i 条双向航道修建在 a i a_i ai​ 与 b i b_i bi​ 两个星球之间，任意飞船驶过它所花费的时间为 t i t_i ti​。数据保证 1 ≤ a i , b i ≤ n 1 \leq a_i,b_i \leq n 1≤ai​,bi​≤n 且 0 ≤ t i ≤ 1000 0 \leq t_i \leq 1000 0≤ti​≤1000。

接下来 m m m 行描述运输计划的情况，其中第 j j j 行包含两个正整数 u j u_j uj​ 和 v j v_j vj​，表示第 j j j 个运输计划是从 u j u_j uj​ 号星球飞往 v j v_j vj​号星球。数据保证 1 ≤ u i , v i ≤ n 1 \leq u_i,v_i \leq n 1≤ui​,vi​≤n

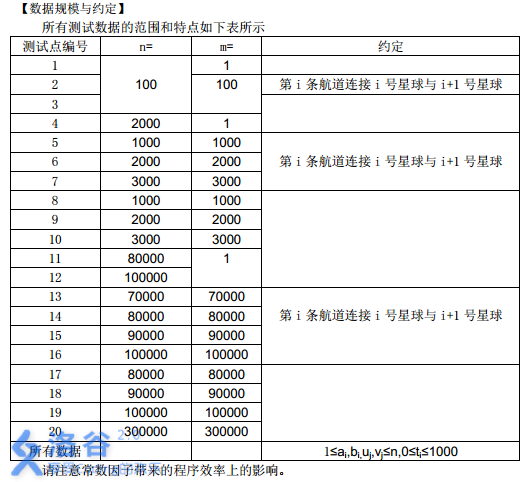
所有测试数据的范围和特点如下表所示

请注意常数因子带来的程序效率上的影响。

Output:

一个整数，表示小 P P P 的物流公司完成阶段性工作所需要的最短时间。

Sample Input:

6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5

Sample Output:

11

题目链接

首先需要计算运输计划的所有路径长度，之后按照升序排列，二分路径长度（工作时间）。

若路径长度大于当前二分Mid，需要记录路径上的边被经过的此数（使用树上差分计次），枚举所有计划都经过的边（Cnt[i] == Num），判断最大运输代价减去边权是否小于Mid。

这道题目不使用快读会TLE一组最大的数据。

AC代码:

#include <bits/stdc++.h>
using namespace std;

namespace FastIO {
    const int MX = 4e7;
    char buf[MX];
    int c, sz;
    void begin() {
        c = 0;
        sz = fread(buf, 1, MX, stdin);
    }
    template <class T>
    inline bool read(T &t) {
        while (c < sz && buf[c] != '-' && (buf[c] < '0' || buf[c] > '9')) {
            c++;
        }
        if (c >= sz) {
            return false;
        }
        bool flag = 0;
        if (buf[c] == '-') {
            flag = 1;
            c++;
        }
        for (t = 0; c < sz && '0' <= buf[c] && buf[c] <= '9'; ++c) {
            t = t * 10 + buf[c] - '0';
        }
        if (flag) {
            t = -t;
        }
        return true;
    }
};

const int maxn = 3e5 + 5;

struct Edge {
    int V, Weight, Next;
};

Edge edges[maxn << 1];
int Head[maxn];
int Tot;

void Init() {
    Tot = 0;
    memset(Head, -1, sizeof(Head));
}

void AddEdge(int U, int V, int Weight) {
    edges[Tot] = Edge {V, Weight, Head[U]};
    Head[U] = Tot++;
}

struct LCAOnline {
    int Rmq[maxn << 1];
    int Vertex[maxn << 1];
    int First[maxn];
    int Parent[maxn];
    int Dis[maxn];
    int LCATot;
    
    int Dp[maxn << 1][20];

    void Work(int N) {
        for (int i = 1; i <= N; ++i) {
            Dp[i][0] = i;
        }
        for (int j = 1; (1 << j) <= N; ++j) {
            for (int i = 1; i + (1 << j) - 1 <= N; ++i) {
                Dp[i][j] = Rmq[Dp[i][j - 1]] < Rmq[Dp[i + (1 << (j - 1))][j - 1]] ? Dp[i][j - 1] : Dp[i + (1 << (j - 1))][j - 1];
            }
        }
    }

    void Dfs(int Cur, int Pre, int Depth) {
        Vertex[++LCATot] = Cur;
        First[Cur] = LCATot;
        Rmq[LCATot] = Depth;
        Parent[Cur] = Pre;
        for (int i = Head[Cur]; ~i; i = edges[i].Next) {
            if (edges[i].V == Pre) {
                continue;
            }
            Dis[edges[i].V] = Dis[Cur] + edges[i].Weight;
            Dfs(edges[i].V, Cur, Depth + 1);
            Vertex[++LCATot] = Cur;
            Rmq[LCATot] = Depth;
        }
    }

    int Query(int Left, int Right) {
        if (Left > Right) {
            swap(Left, Right);
        }
        int Len = int(log2(Right - Left + 1));
        return Rmq[Dp[Left][Len]] <= Rmq[Dp[Right - (1 << Len) + 1][Len]] ? Dp[Left][Len] : Dp[Right - (1 << Len) + 1][Len];
    }
    
    void Init(int Root, int NodeNum) {
        memset(Dis, 0, sizeof(Dis));
        LCATot = 0;
        Dfs(Root, 0, 0);
        Parent[1] = 0;
        Work(2 * NodeNum - 1);
    }

    int GetDis(int U, int V) {
        return Dis[U] + Dis[V] - 2 * Dis[LCA(U, V)];
    }

    int LCA(int U, int V) {
        return Vertex[Query(First[U], First[V])];
    }
}LCA;

struct Query {
    int U, V, LCA, Dis;

    bool operator < (const Query &B) const {
        return Dis < B.Dis;
    }
};

int N, M;
int Left, Right;
int Ans;
int Cnt[maxn];
Query querys[maxn];

int Dfs(int Cur, int Pre) {
    for (int i = Head[Cur]; ~i; i = edges[i].Next) {
        if (edges[i].V == Pre) {
            continue;
        }
        Cnt[Cur] += Dfs(edges[i].V, Cur);
    }
    return Cnt[Cur];
}

bool Check(int X) {
    int Num = 0, MaxDis = 0;
    memset(Cnt, 0, sizeof(Cnt));
    for (int i = 1; i <= M; ++i) {
        if (querys[i].Dis <= X) {
            continue;
        }
        Cnt[querys[i].U]++; Cnt[querys[i].V]++;
        Cnt[querys[i].LCA] -= 2;
        MaxDis = max(MaxDis, querys[i].Dis - X);
        Num++;
    }
    Dfs(1, 0);
    for (int i = 1; i <= N; ++i) {
        if (Cnt[i] == Num && LCA.GetDis(i, LCA.Parent[i]) >= MaxDis) {
            return true;
        }
    }
    return false;;
}

int main(int argc, char *argv[]) {
    FastIO::begin();
    Init();
    FastIO::read(N); FastIO::read(M);
    for (int i = 1, A, B, T; i < N; ++i) {
        FastIO::read(A); FastIO::read(B); FastIO::read(T);
        AddEdge(A, B, T);
        AddEdge(B, A, T);
    }
    LCA.Init(1, N);
    memset(Cnt, 0, sizeof(Cnt));
    Right = 0;
    for (int i = 1; i <= M; ++i) {
        FastIO::read(querys[i].U); FastIO::read(querys[i].V);
        querys[i].LCA = LCA.LCA(querys[i].U, querys[i].V);
        querys[i].Dis = LCA.GetDis(querys[i].U, querys[i].V);
        Right = max(Right, querys[i].Dis);
    }
    sort(querys + 1, querys + M + 1);
    Left = 0; Ans = 0;
    while (Left <= Right) {
        int Mid = (Left + Right) >> 1;
        if (Check(Mid)) {
            Ans = Mid;
            Right = Mid - 1;
        }
        else {
            Left = Mid + 1;
        }
    }
    printf("%d\n", Ans);
    return 0;
}