目前已更新:第一题,第二题,第四题
1. 最大子序和(变体)
题目描述:

首先考虑常规的最大子序和的问题,即不能去掉中间的一段,leetcode上有一个这样 的题目:
分析如下:
考虑数组中某一位置的元素
nums[i],如果nums[i] + (i 前面若干个连续数组成的累计和) > nums[i],则表示加上nums[i]之后会组成更大的子序和,我们就把相加值赋给nums[i],反之,则不动nums[i]的值,这之后的nums[i]表示:从前往后遍历,到i 这个位置时的最大子序和(注意:nums[i]必须在包含里面,表示包含nums[i]的最大子序和,而不是nums[:i+1]的最大子序和)。参考下图:
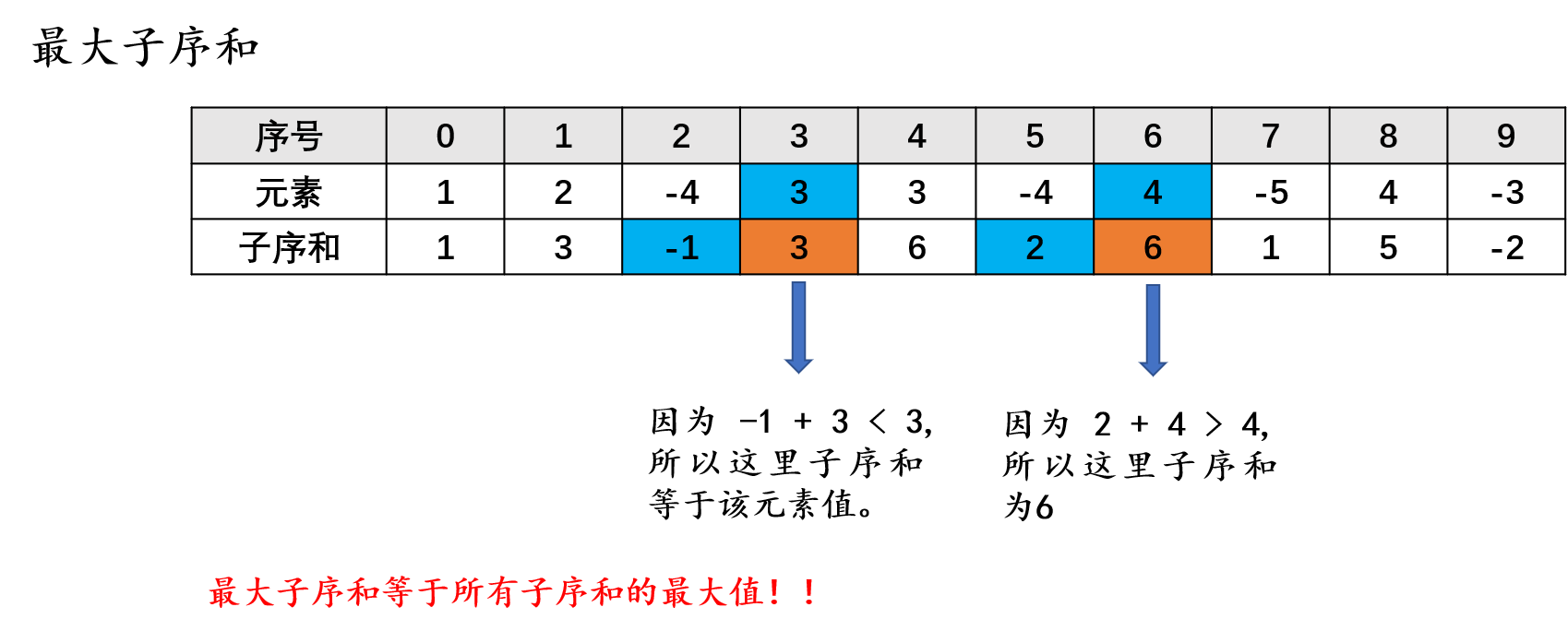
而我们这个问题有个附加条件:可以去掉中间的一段。
假如我们随便去掉中间的一段,则数组被分成两段(数组1,数组2):
最大子序和 = 数组1从前往后遍历的最大子序和 + 数组2从后往前遍历的最大子序和
这里有一个问题就是如果数组1最大子序和不是出现在数组1最后的位置,还等价吗?其实是等价的,相当于多去掉一段,并不影响结果。因此,代码可以写成:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
nums = [0] + nums # 加一个0是为了防止全负数的情况,这种情况下则不包含任何元素,子序和为0
nums1 = nums[:]
nums1.reverse() # 复制一份,并反转数组
n = len(nums)
for i in range(1,n):
nums[i] = max(nums[i],nums[i-1]+nums[i]) # 从前往后的最大子序和
nums1[i] = max(nums1[i],nums1[i-1]+nums1[i]) # 从后往前的最大子序和
# 遍历数组,找最大值
max_ = 0
for i in range(n-1):
for j in range(0, n-i-1):
max_ = max(max_, nums[i]+nums1[j])
print(nums,nums1)
return max_2. 矩阵求乘积最大
题目描述:

这一题可以简化,以其中的两行为例:
若第一行的最大值的序号与第二行的最大值的序号互异,则这两行
乘积的最大值为两行分别的最大值相乘;若第一行的最大值得序号与第二行的最大值的序号相等,说明某一行的最大值的序号与另一行的第二大值得序号必互异,则
乘积最大值在某一行的最大值与另一行的第二大的值的乘积当***有两个,取最大的)
代码如下:
nums = [[1,2,3,4], [5,6,7,8], [9,10,11,12]]
n = len(nums)
m = len(nums[0])
target = []
for i in range(n):
tmp = [[-float("inf"), -1], [-float("inf"), -1]] # 存储当前行的最大值,第二大的值以及他们各自的序号
for j in range(m):
if nums[i][j] > tmp[0][0]:
tmp[1] = tmp[0][:]
tmp[0][0] = nums[i][j]
tmp[0][1] = j
target.append(tmp)
max_ = -float("inf")
for i in range(n):
for j in range(i+1,n):
if target[i][0][1] != target[j][0][1]: # 如果最大值两个序号不相等,则这两行的最大值是两行各自最大值的乘积
max_ = max(target[i][0][0]*target[j][0][0], max_)
else: # 反之则说明这两行中某一行的最大值的序号和另一行的第二大的值的序号是互异的
max_ = max(target[i][0][0]*target[j][1][0], target[i][1][0]*target[j][0][0], max_)
print(max_)3. 逐渐平均——值最大
题目描述:

这题思路很简单:
- 首先要明确一点,最先加入的数被除的次数最多,比如第一个数,他就相当于除以了
2^(n-1),每次除,这个数都会减少一半。基于这个思想,我们要做到的是,要让最大的数尽量少被除,因此我们可以先排序,然后一遍遍历就可以解决。
代码如下:
nums = [4,5,2,6,1,7,5,9]
nums.sort()
target = round(nums[0],4)
for i in range(1,len(nums)):
target = round((target + nums[i])/2, 4)
print(target)




 京公网安备 11010502036488号
京公网安备 11010502036488号