poj 2559 Largest Rectangle in a Histogram(单调栈)

题目描述

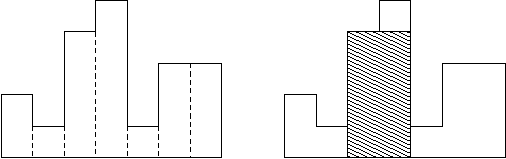
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, …, hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

解题思路：

这个题是单调栈的经典应用题了。
首先想到暴力的做法是枚举每一个矩形，以他的高度设为我们答案矩形的高度，然后向两边扩散，直到扩散到其左边和右边分别都有一个矩形高度小于我们当前答案矩形的高度（或扩散遇到边界）为止，然后计算出面积，取最大值。这样的算法复杂度为 $O (n^{2})$ 。

我们如果想要优化这个暴力的算法，那下手的点就在优化扩散的速度这里，因为很明显我们暴力的算法中每一个矩形扩散的区域有很多重合的，造成了低效。

应用单调栈的算法让每个矩形依次入栈，栈中的元素记录两个关键字：矩形的高度，矩形的最大向左扩散宽度。而每个矩形入栈的方式是以维护单调栈的形式来进行的：当一个新元素入栈时，我们把栈内所有大于等于新元素的元素弹出，然后再把新元素压入栈。这样栈内元素总是递增的，我们把元素弹出栈的时候会发现元素按弹出的顺序总是递减的。

所以，当我们把一个新矩形压入栈时，本身栈内元素高度是单增的，那么新元素的最大左扩散宽度不会包含当前栈顶所包含的宽度，因为栈顶要求比新元素矮，新元素才能直接入栈；
但是当栈顶高度比新元素高的时候，就要依次弹出那些比新元素高的元素，而新元素是可以扩散到这些他左边比他高的元素的，所以我们在弹出他们的同时，把他们的最大左宽度累加到新元素的最大左宽度上。

我们再看栈内的元素，对于每个元素，向栈底的都比他矮，宽度扩散不过去，向栈顶的都比他高，可以扩散过去，所以每个元素的最大向右扩散宽度就是他向栈顶的所有元素的宽度和。那么当因为新元素入栈导致有元素出栈时，新元素比这些出栈元素矮，那么这些元素向右只能扩散到新元素了，那我们就从当前栈顶开始，累加每一个弹出元素的宽度，作为每个弹出元素的最大右宽度，出栈时把左宽度与右宽度加起来就是这个矩形的总宽度，这个矩形就可以计算面积，与历史取最大值。

总结一下：
1.单调栈工作方式：新元素比栈顶大，入栈；新元素比栈顶小，弹出栈顶，再判断新栈顶大小，重复，直至所有比新元素大的元素弹出，新元素入栈
2.基于单调栈，栈内每个元素左宽度不重合，右宽度为到栈顶的宽度和
3.当新元素入栈引发元素出栈时，每个出栈元素的右宽度最大，因此其最大扩散宽度确定，可以计算最大扩散面积
4.当新元素入栈引发元素出栈时，最后一个出栈元素的右宽度就是新元素最大左宽度，要累加到新元素上

这样，我们让所有矩形依次入栈，然后再把栈内元素依次出栈，这个过程就可以统计最大面积了，复杂度为 $O (n)$ 。

AC代码：

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <map>
#include <queue>
#include <stack>
#include <string>
#include <set>
#include <vector>
#include <bitset>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const long long LINF = 1e14;
const double PI = acos(-1.0);
const int MAXN = 3e5+10;

struct node
{
    int height, width; //高度，最大左宽度
    node(int h = 0, int w = 0): height(h), width(w) {};
};

stack<node> s;

int main()
{
    int n, h;
    while(~scanf("%d", &n) && n)
    {
        ll ans = 0, cur, tWidth; //答案，当前矩形最大扩散面积，出栈元素宽度累计
        for(int i = 0; i <= n; i++)
        {
            if(i < n) scanf("%d", &h);
            else h = 0; //多入栈一个0，使所有元素弹出
            tWidth = 0;
            while(!s.empty() && s.top().height >= h)
            {
                cur = s.top().height * (s.top().width + tWidth);
                ans = max(ans, cur);
                tWidth += s.top().width;
                s.pop();
            }
            s.push(node(h, tWidth + 1));
        }
        printf("%lld\n", ans);
    }
    return 0;
}