Codeforces Round 1006 (Div. 3)A-F题解

A. New World, New Me, New Array（签到，模拟）

给你一个n,k,p,并且给定一个长度为n，初始值全为0的a数组，每次操作可以让数组里的任意一个数变成-p 到 p的任意一个数，问你最少需要多少次操作使得a数组和为k.

签到题，直接贪心就好了

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int MOD=998244353;
const int N=1000100;

void init() {
   

}

int a[N];
int pre[N];

void solve() {
   
    init();

    int n,k,p;
    cin>>n>>k>>p;
    if(k < (-p) * n || k > p * n) {
   
        cout<<-1<<"\n";
        return ;
    }

    if(k<0) {
   
        cout<<k / (-p) + (k % (-p)!=0)<<"\n";
    }
    else {
   
        cout<< k / p + (k % p != 0)<<"\n";
    }
}


signed main() {
   
     //ios::sync_with_stdio(false);
     //cin.tie(0);
     //cout.tie(0);

    int t=1;
    cin>>t;

    while(t--) {
   
        solve();
    }
    return 0;
}

B. Having Been a Treasurer in the Past, I Help Goblins Deceive（签到，贪心）

给定你’-'字符的个数和 '_'字符的个数，让你构造一个字符串使得子串最大的情况。

签到题，根据基本不等式就可以知道最优情况就是将’-‘字符分为两半放两边，’_'字符全部放中间就好。

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int MOD=998244353;
const int N=1000100;


void init() {
   

}

int a[N];
int pre[N];

void solve() {
   
    init();

    int n;
    cin>>n;
    int num1=0;
    int num2=0;
    int sum=0;

    string s;
    cin>>s;
    for(int i=0;i<n;i++) {
   
        if(s[i]=='-') sum++;
    }

    num1 = sum/2;
    num2 = sum - num1;

    cout << num1 * num2 * (n - sum)<<"\n";
}


signed main() {
   
     //ios::sync_with_stdio(false);
     //cin.tie(0);
     //cout.tie(0);

    int t=1;
    cin>>t;

    while(t--) {
   
        solve();
    }
    return 0;
}

C. Creating Keys for StORages Has Become My Main Skill（贪心+模拟）

给你一个n和一个x,要求你构造一个长度为n的数组a，其中所有数的和运算结果为x,而且要求整个数组的mex（最小未出现自然数）是所有能够让和运算为x结果中最大的。

其实看到要求mex最大就应该有思路了，直接从0开始按顺序来，最后记得加上x就好，这就是贪心的想法。注意当按顺序遍历到比x大的数字或者当前数字存在某个位有1而x没有，那就要停止遍历

还是挺简单的一个模拟的

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int MOD=998244353;
const int N=1000100;

void init() {
   

}

int a[N];
int pre[N];

void solve() {
   
    init();

    int n,x;
    cin>>n>>x;

    if(n==1) {
   
        cout<<x<<"\n";
        return ;
    }

    map<int,int>mp;
    int sum=0;
    for(int i=30;i>=0;i--) {
   
        int now = (1 << i);
        if((now & x) != 0) {
   
            mp[i]=1;
            sum++;
        }
    }

    int tim=0;
    for(int i=0;i<n-1;i++) {
   

        int sign=1;
        for(int j=30;j>=0;j--) {
   
            int now = (1 << j);
            if((now &i)  == 0) continue;
            if((now & x) != 0)//说明这个位是x有的
            {
   
                if(mp[j]) {
   
                    mp[j]=0;
                    sum--;
                }
            }
            else {
   
                sign=0;
                break;
            }
        }
        if(sign || sum==0) {
   
            cout<<min(i,x)<<" ";
            tim++;
        }
        else break;
    }
    int sign=1;

    if(tim == n-1) {
   
        for(int i=30;i>=0;i--) {
   
            int now = (1 << i);
            if((now & tim)!=0) {
   
                if((now & x)==0) {
   
                    sign=0;
                    break;
                }
                else {
   
                    if(mp[i]) {
   
                        sum--;
                    }
                }
            }
        }
    }

    if(sign && sum == 0) {
   
        for(int i=tim;i<n;i++) cout<<i<<" ";
    }

    else {
   
        for(int i=1;i<=n-tim;i++) cout<<x<<" ";
    }
    cout<<"\n";
}


signed main() {
   
     //ios::sync_with_stdio(false);
     //cin.tie(0);
     //cout.tie(0);

    int t=1;
    cin>>t;

    while(t--) {
   
        solve();
    }
    return 0;
}

D. For Wizards, the Exam Is Easy, but I Couldn’t Handle It(构造)

给定你一个数组a，你必须只能进行一次操作，选定一个l,r，然后会将a数组l到r区间进行一次逆时针旋转，如图：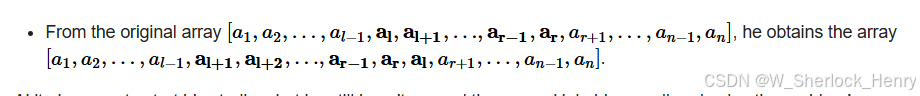
要求你进行完操作之后能让a数组的逆序对数最少，问你选定的l,r

仔细想想就能想到，这个操作只会让选定区间最前面的数字跑到最后面，所以直接预处理一遍第i个数作第一个数字，然后遍历当第i个数为第一个数字时候，哪个位置为最优终点，遍历过程中要注意如果第j个数字比ai大的话贡献就要减一（相当于第i个数跑到第j个数字之后就会多一个逆序对数，反之同理），如果第j个数字比ai小的话贡献加一。

代码如下：

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int MOD=998244353;
const int N=1000100;

void init() {
   

}

int a[N];
int pre[N];

void solve() {
   
    init();

    int n;
    cin>>n;
    for(int i=1;i<=n;i++) {
   
        cin>>a[i];
    }

    map<int,int>mp;//记录对于第i个数作为第一个数字的时候最大贡献为多少
    map<int,int>pos;

    for(int i=1;i<=n;i++) {
   
        int nowsum = 0;

        for(int j=i+1;j<=n;j++) {
   
            if(a[j] < a[i]) {
   
                nowsum ++;
                if(nowsum > mp[i]) {
   
                    mp[i] = nowsum;
                    pos[i] = j;
                }
            }
            else if(a[j] > a[i]) {
   
                nowsum --;
            }
        }

    }

    int maxvalue = 0;
    int maxpos=0;
    int maxback=0;

    for(int i=1;i<=n;i++) {
   
        if(mp[i] > maxvalue) {
   
            maxvalue = mp[i];
            maxpos = i;
            maxback=pos[i];
        }
    }
    if(maxvalue ==0) {
   
        cout<<1<<" "<<1<<"\n";
        return ;
    }
    else {
   
        cout<<maxpos<<" "<<maxback<<"\n";
    }

}


signed main() {
   
     //ios::sync_with_stdio(false);
     //cin.tie(0);
     //cout.tie(0);

    int t=1;
    cin>>t;

    while(t--) {
   
        solve();
    }
    return 0;
}

E. Do You Love Your Hero and His Two-Hit Multi-Target Attacks?(贪心)

给你一个整数k,要求你自己选定一个n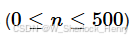，要求满足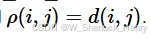的对数为k,其中。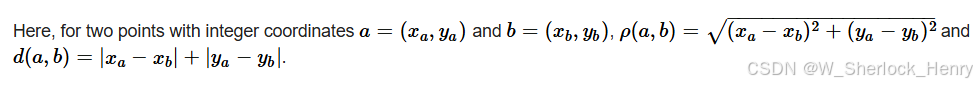
联系三角形不等式可知，这里就是要求有k对共线坐标。我们可以贪心想想，我们能否只让他们横着共线，然后再想想，2，3，4，5个坐标共线的时候，共线坐标对数分别为1，3，6，10.我们会发现这个其实就是组合数，然后这个数组就是n * (n-1) / 2，由于有1的存在，那么我们肯定能够用这个数组里的数字拼凑成k.

所以我们只要像二进制，十进制构造数字一样，不断尽可能用最大的数字去构造即可。就比如k=14，我就可以先让共线对数分别为 10 3 1，也就是让第一行有5个坐标，第二行有3个坐标，第三行有2个坐标即可、

要注意一点就是竖着不要共线

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int MOD=998244353;
const int N=1000100;

void init() {
   

}

int a[N];
int pre[N];

void solve() {
   
    init();

    int k;
    cin>>k;

    if(k == 0) {
   
        cout<<0<<"\n";
        return;
    }

    int nowx=0,nowy=0;
    queue< pair<int,int> >q;
    while(k) {
   
        int maxvalue = 0;
        for(int i=2;i<=500;i++) {
   
            if(k >= pre[i]) {
   
                maxvalue = i;
            }
            else break;
        }
        for(int i=1;i<=maxvalue;i++) {
   
            q.push({
   nowx,nowy++});
        }
        nowx++;
        k-=pre[maxvalue];
    }
    cout<<q.size()<<"\n";
    while(!q.empty()) {
   
        auto now = q.front();
        cout<<now.first<<" "<<now.second<<"\n";
        q.pop();
    }

}


signed main() {
   
     //ios::sync_with_stdio(false);
     //cin.tie(0);
     //cout.tie(0);

	//预处理i个坐标共线的时候有多少个共线坐标对数
    int now=1;
    for(int i=2;i<=500;i++) {
   
        pre[i] = pre[i-1] + now;
        now++;
        if(pre[i] > 100000) break;
    }

    int t=1;
    cin>>t;

    while(t--) {
   
        solve();
    }
    return 0;
}

F. Goodbye, Banker Life（数论+guess）

给你一个三角形，第i行有i个数字，第一行第一个数为x，第i行第一个数等于上一行第一个数，第i行最后一个数就等于上一行最后一个数，然后第i行第j个数就是.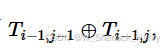

让你输出第n行的所有数字

这道题其实就看你能不能想到一个点，就是杨辉三角形。题面这个描述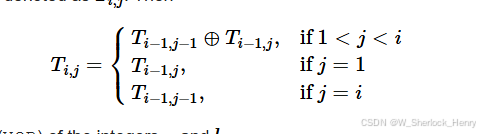
其实形如杨辉三角形。我们不妨想想这道题和杨辉三角形的关系。

不难发现，数组里的数字要么是x要么是0，想想就能知道，对于中间的数，如果进行了偶数次和x异或，那就是0，如果进行了奇数次和x异或计算，那就是x。其中当前位置和x进行的异或计算次数相当于 $T_{i-1,j-1}$ + $T_{i-1,j}$ 。

那我们就可以转到杨辉三角形，杨辉三角形还有一个很重要的性质就是组合数，由于n的范围是1e6，如果直接计算就会爆 ，我们就要考虑优化的方法。我们知道$C_n^i$ = $C_n^{i-1}$ * (n-i+1) / i。
那么我们只要知道分子总共有多少个2，分母有多少个2，就能知道当前数字是偶数还是奇数

代码如下：

#include<bits/stdc++.h>

using namespace std;

#define int long long

const int MOD=998244353;
const int N=1000100;

void init() {
   

}

int a[N];
int pre[N];

void solve() {
   
    init();

    int n,x;
    cin>>n>>x;

    if(n==1) {
   
        cout<<x<<"\n";
        return ;
    }


    int sum1=0;
    int sum2=0;
    int now = n-1;

    cout<<x<<" ";

    for(int i=1;i<=n-1;i++) {
   
        int num=n-i;
        while(num % 2 ==0) {
   
            num /= 2;
            sum1++;
        }
        num = i;
        while(num % 2 ==0) {
   
            num /= 2;
            sum2++;
        }
        if(sum1 > sum2) cout<<0<<" ";
        else cout<<x<<" ";
    }
    cout<<"\n";
}


signed main() {
   
     //ios::sync_with_stdio(false);
     //cin.tie(0);
     //cout.tie(0);

    int now=1;
    for(int i=2;i<=500;i++) {
   
        pre[i] = pre[i-1] + now;
        now++;
        if(pre[i] > 100000) break;
    }

    int t=1;
    cin>>t;

    while(t--) {
   
        solve();
    }
    return 0;
}