在学习这个算法之前需要很多先验算法,首先来学习一下OTSU大津法。
OTSU算法原理
OYTSU大津法,再次看到这个算法,不禁想到了一个故事,去年大四上学期在学习数字图像处理课程上时,被老师抽到回答问题,还给老师指出OTSU算法可以通过打表的方式将复杂度从O(n^2)降为O(n),物是人非了,那个引起我兴趣的老师啊,听说已经南下珠江三角洲教书了,看他的消息仿佛也是因为工资的问题,只想说真的伤感啊。一心做研究的学者,反而是赚不到什么钱了。。。扯多了。OTSU算法要解决的问题要把前景和背景分开,使用了聚类的思想,将图像的灰度数按灰度级分成2个部分,使得2个部分之间的灰度值差异最小,通过方差的计算来寻找一个合适的灰度级别来划分。OTSU算法的计算简单,不受到图像亮度和对比度的影响。因此,使得类间方差最大的分割意味着错分概率最小。
OTSU算法步骤
设t为灰度级门槛值,从L个灰度级遍历t,使得t为某个值的时候,前景和背景的方差最大,则,这个t值便是我们要求育德门槛值。对于w0(分开后前景像素点占图像像素比例,u0分开后前景像素点的平均灰度,w1分开后背景像素点数占图像比例,u1表示分开后背景像素点的平均灰度),图像的总灰度定义为: u=w0∗u0+w1∗u1,方法计算公式为: g=w0∗(u0−w0)∗(u0−w0)+w1∗(u1−u)∗(u1−u),把这个公式展开化简为 g=w0∗w1∗(u0−u1)∗(u0−u1),由于OTSU算法诗对图像的灰度级进行聚类,所以第一步应该计算出直方图。
OTSU代码实现
int OTSU(Mat src){
int row = src.rows;
int col = src.cols;
int PixelCount[256]={0};
float PixelPro[256]={0};
int total_Pixel = row * col;
float threshold = 0;
//统计灰度级中每个像素在整副图中的个数
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
PixelCount[src.at<int>(i, j)]++;
}
}
//计算每个像素在整副图中的个数
for(int i = 0; i < 256; i++){
PixelPro[i] = (float)(PixelCount[i]) / (float)(total_Pixel);
}
//遍历灰度级[0,255],计算出方差最大的灰度值,为最佳阈值
float w0, w1, u0tmp, u1tmp, u0, u1, u, deltaTmp, deltaMax = 0;
for(int i = 0; i < 256; i++){
w0 = w1 = u0tmp = u1tmp = u0 = u1 = u = deltaTmp = 0;
for(int j = 0; j < 256; j++){
if(j <= i){//以i为阈值分类,第一类总的概率
w0 += PixelPro[j];
u0tmp += j * PixelPro[j];
}else{//前景部分
w1 += PixelPro[j];
u1tmp += j * PixelPro[j];
}
}
u0 = u0tmp / w0; //第一类的平均灰度
u1 = u1tmp / w1; //第二类的平均灰度
u = u0 + u1; //整副图像的平均灰度
//计算类间方差
deltaTmp = w0 * (u0 - u) * (u0 - u) + w1 * (u1 - u) * (u1 - u);
//找出最大类间方差以及对应阈值
if(deltaTmp > deltaMax){
deltaMax = deltaTmp;
threshold = i;
}
}
return threshold;
}
Canny算子边缘检测步骤
- 使用高斯滤波算法,以平滑图像,滤除噪声
- 计算图像中每个像素点的梯度强度和方向
- 应用非极大值抑制,以消除边缘检测带来的杂散响应
- 应用双阈值检测来确定真正的边缘和潜在的边缘
- 通过抑制孤立的弱边缘最终完成边缘检测
对应算法步骤的原理
- 高斯滤波:这个我之前已经讲过了,可以看我之前博客。
- 计算梯度强度和方向:
利用Sobel算子返回水平Gx和垂直Gy的一阶导数值。以此来计算梯度强度G和方向thead。 G=Gx2+Gy2, θ=arctan(GxGy), Gx=∑i∑jSobelxi,j∗imgi,j, Gy=∑i∑jSobelyi,j∗imgi,j
-应用非极大值抑制,以消除边缘检测带来的杂散响应,非极大值抑制是一种边缘稀疏技术,作用在于"瘦边"。对图片进行梯度计算之后,仅仅基于梯度值提取的边缘仍然比较模糊。对于标准3,对边缘有且应当只有一个准确的响应。而非极大值抑制则可以帮助将将局部最大值之外的所有梯度值抑制为0,对梯度图像中每个像素进行非极大值抑制的算法步骤为: - 1.将当前像素的梯度强度与沿正负梯度方向上的两个像素进行比较。
- 2.如果当前像素的梯度值与另外两个像素值相比最大,则该像素点保留为边缘点,否则该像素点被抑制。通常
为了更加精确的计算,在跨梯度方向的两个相邻像素之间只用线性插值来得到要比较的像素梯度,举例为:
- 双阈值检测
在施加非极大值抑制之后,剩余的像素可以更准确地表示图像中的实际边缘。然而,仍然存在由于噪声和颜色变化引起的一些边缘像素。为了解决这些杂散响应,必须用弱梯度值过滤边缘像素,并保留具有高梯度值的边缘像素,可以通过选择高低阈值来实现。如果边缘像素的梯度值高于高阈值,则将其标记为强边缘像素;如果边缘像素的梯度值小于高阈值并且大于低阈值,则将其标记为弱边缘像素;如果边缘像素的梯度值小于低阈值,则会被抑制。阈值的选择取决于给定输入图像的内容。 - 高低阈值分别为heightThes 和 lowThes.
确定阈值方法有:全局阈值、Otsu等方法
-到目前为止,被划分为强边缘的像素点已经被确定为边缘,因为它们是从图像中的真实 边缘中提取出来的。然而,对于弱边缘像素,将会有一些争论,因为这些像素可以从真实边缘提取也可以是因噪声或颜色变化引起的。为了获得准确的结果,应该抑制由后者引起的弱边缘。通常,由真实边缘引起的弱边缘像素将连接到强边缘像素,而噪声响应未连接。为了跟踪边缘连接,通过查看弱边缘像素及其8个邻域像素,只要其中一个为强边缘像素,则该弱边缘点就可以保留为真实的边缘。
抑制孤立边缘点的伪代码描述如下:
C++源码实现
const double PI = 3.1415926;
double getSum(Mat src){
double sum = 0;
for(int i = 0; i < src.rows; i++){
for(int j = 0; j < src.cols; j++){
sum += (double)src.at<double>(i, j);
}
}
return sum;
}
Mat CannyEdgeDetection(cv::Mat src, int kSize, double hightThres, double lowThres){
// if(src.channels() == 3){
// cvtColor(src, src, CV_BGR2GRAY);
// }
cv::Rect rect;
Mat gaussResult;
int row = src.rows;
int col = src.cols;
printf("%d %d\n", row, col);
Mat filterImg = Mat::zeros(row, col, CV_64FC1);
src.convertTo(src, CV_64FC1);
Mat dst = Mat::zeros(row, col, CV_64FC1);
int gaussCenter = kSize / 2;
double sigma = 1;
Mat guassKernel = Mat::zeros(kSize, kSize, CV_64FC1);
for(int i = 0; i < kSize; i++){
for(int j = 0; j < kSize; j++){
guassKernel.at<double>(i, j) = (1.0 / (2.0 * PI * sigma * sigma)) * (double)exp(-(((double)pow((i - (gaussCenter+1)), 2) + (double)pow((j-(gaussCenter+1)), 2)) / (2.0*sigma*sigma)));
}
}
Scalar sumValueScalar = cv::sum(guassKernel);
double sum = sumValueScalar.val[0];
guassKernel = guassKernel / sum;
for(int i = gaussCenter; i < row - gaussCenter; i++){
for(int j = gaussCenter; j < col - gaussCenter; j++){
rect.x = j - gaussCenter;
rect.y = i - gaussCenter;
rect.width = kSize;
rect.height = kSize;
//printf("%d %d\n", i, j);
//printf("%d %d %.5f\n", i, j, cv::sum(guassKernel.mul(src(rect))).val[0]);
filterImg.at<double>(i, j) = cv::sum(guassKernel.mul(src(rect))).val[0];
}
}
Mat gradX = Mat::zeros(row, col, CV_64FC1); //水平梯度
Mat gradY = Mat::zeros(row, col, CV_64FC1); //垂直梯度
Mat grad = Mat::zeros(row, col, CV_64FC1); //梯度幅值
Mat thead = Mat::zeros(row, col, CV_64FC1); //梯度角度
Mat whereGrad = Mat::zeros(row, col, CV_64FC1);//区域
//x方向的Sobel算子
Mat Sx = (cv::Mat_<double>(3, 3) << -1, 0, 1, -2, 0, 2, -1, 0, 1);
//y方向的Sobel算子
Mat Sy = (cv::Mat_<double >(3, 3) << 1, 2, 1, 0, 0, 0, -1, -2, -1);
//计算梯度赋值和角度
for(int i=1; i < row-1; i++){
for(int j=1; j < col-1; j++){
rect.x = j-1;
rect.y = i-1;
rect.width = 3;
rect.height = 3;
Mat rectImg = Mat::zeros(3, 3, CV_64FC1);
filterImg(rect).copyTo(rectImg);
//梯度和角度
gradX.at<double>(i, j) += cv::sum(rectImg.mul(Sx)).val[0];
gradY.at<double>(i, j) += cv::sum(rectImg.mul(Sy)).val[0];
grad.at<double>(i, j) = sqrt(pow(gradX.at<double>(i, j), 2) + pow(gradY.at<double>(i, j), 2));
thead.at<double>(i, j) = atan(gradY.at<double>(i, j)/gradX.at<double>(i, j));
if(0 <= thead.at<double>(i, j) <= (PI/4.0)){
whereGrad.at<double>(i, j) = 0;
}else if(PI/4.0 < thead.at<double>(i, j) <= (PI/2.0)){
whereGrad.at<double>(i, j) = 1;
}else if(-PI/2.0 <= thead.at<double>(i, j) <= (-PI/4.0)){
whereGrad.at<double>(i, j) = 2;
}else if(-PI/4.0 < thead.at<double>(i, j) < 0){
whereGrad.at<double>(i, j) = 3;
}
}
}
//printf("success\n");
//梯度归一化
double gradMax;
cv::minMaxLoc(grad, &gradMax);
if(gradMax != 0){
grad = grad / gradMax;
}
//双阈值确定
cv::Mat caculateValue = cv::Mat::zeros(row, col, CV_64FC1); //grad变成一维
resize(grad, caculateValue, Size(1, grad.rows * grad.cols));
cv::sort(caculateValue, caculateValue, CV_SORT_EVERY_COLUMN + CV_SORT_ASCENDING);//升序
long long highIndex= row * col * hightThres;
double highValue = caculateValue.at<double>(highIndex, 0); //最大阈值
double lowValue = highValue * lowThres;
//NMS
for(int i = 1 ; i < row-1; i++ ){
for( int j = 1; j<col-1; j++){
// 八个方位
double N = grad.at<double>(i-1, j);
double NE = grad.at<double>(i-1, j+1);
double E = grad.at<double>(i, j+1);
double SE = grad.at<double>(i+1, j+1);
double S = grad.at<double>(i+1, j);
double SW = grad.at<double>(i-1, j-1);
double W = grad.at<double>(i, j-1);
double NW = grad.at<double>(i -1, j -1); // 区域判断,线性插值处理
double tanThead; // tan角度
double Gp1; // 两个方向的梯度强度
double Gp2; // 求角度,绝对值
tanThead = abs(tan(thead.at<double>(i,j)));
switch ((int)whereGrad.at<double>(i,j)) {
case 0: Gp1 = (1- tanThead) * E + tanThead * NE; Gp2 = (1- tanThead) * W + tanThead * SW; break;
case 1: Gp1 = (1- tanThead) * N + tanThead * NE; Gp2 = (1- tanThead) * S + tanThead * SW; break;
case 2: Gp1 = (1- tanThead) * N + tanThead * NW; Gp2 = (1- tanThead) * S + tanThead * SE; break;
case 3: Gp1 = (1- tanThead) * W + tanThead *NW; Gp2 = (1- tanThead) * E + tanThead *SE; break;
default: break;
}
// NMS -非极大值抑制和双阈值检测
if(grad.at<double>(i, j) >= Gp1 && grad.at<double>(i, j) >= Gp2){
//双阈值检测
if(grad.at<double>(i, j) >= highValue){
grad.at<double>(i, j) = highValue;
dst.at<double>(i, j) = 255;
} else if(grad.at<double>(i, j) < lowValue){
grad.at<double>(i, j) = 0;
} else{
grad.at<double>(i, j) = lowValue;
}
} else{
grad.at<double>(i, j) = 0;
}
}
}
//抑制孤立低阈值点 3*3. 找到高阈值就255
for(int i = 1; i < row - 1; i++){
for(int j = 1; j < col - 1; j++){
if(grad.at<double>(i, j) == lowValue){
//3*3 区域强度
rect.x = i-1;
rect.y = j-1;
rect.width = 3;
rect.height = 3;
for(int x = 0; x < 3; x++){
for(int y = 0; y < 3; y++){
if(grad(rect).at<double>(x, y)==highValue){
dst.at<double>(i, j) = 255;
break;
}
}
}
}
}
}
return dst;
}
效果
原图

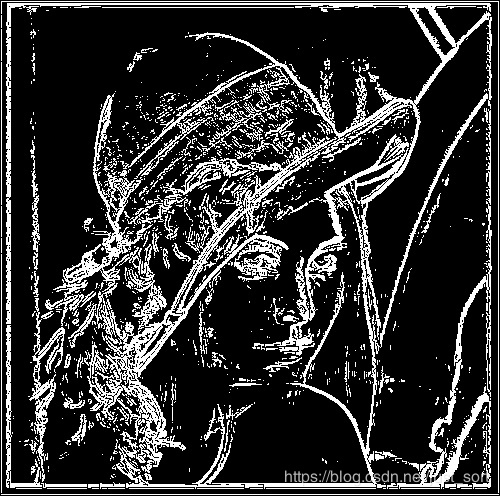
参考文章
https://blog.csdn.net/jmu201521121021/article/details/80622011





 京公网安备 11010502036488号
京公网安备 11010502036488号