2022-11-28：给定两个数组A和B，比如 A = { 0, 1, 1 } B = { 1, 2, 3 }

2022-11-28：给定两个数组A和B，比如 A = { 0, 1, 1 } B = { 1, 2, 3 } A[0] = 0, B[0] = 1，表示0到1有双向道路 A[1] = 1, B[1] = 2，表示1到2有双向道路 A[2] = 1, B[2] = 3，表示1到3有双向道路 给定数字N，编号从0N，所以一共N+1个节点 题目输入一定保证所有节点都联通，并且一定没有环 默认办公室是0节点，其他1N节点上，每个节点上都有一个居民 每天所有居民都去往0节点上班 所有的居民都有一辆5座的车，也都乐意和别人一起坐车 车不管负重是多少，只要走过一条路，就耗费1的汽油 比如A、B、C的居民，开着自己的车来到D居民的位置，一共耗费3的汽油 D居民和E居民之间，假设有一条路 那么D居民可以接上A、B、C，4个人可以用一辆车，去往E的话，就再耗费1的汽油。 求所有居民去办公室的路上，最少耗费多少汽油。 来自微软。

答案2022-11-28：

dfn序。

代码用rust编写。代码如下：

use std::iter::repeat;

fn main() {
    let mut a1 = vec![0, 1, 1];
    let mut b1 = vec![1, 2, 3];
    let n1 = 3;
    println!("ans = {}", min_fuel(&mut a1, &mut b1, n1));

    let mut a2 = vec![1, 1, 1, 9, 9, 9, 9, 7, 8];
    let mut b2 = vec![2, 0, 3, 1, 6, 5, 4, 0, 0];
    let n2 = 9;
    println!("ans = {}", min_fuel(&mut a2, &mut b2, n2));
}

static mut CNT: i32 = 0;

fn min_fuel(a: &mut Vec<i32>, b: &mut Vec<i32>, n: i32) -> i32 {
    // 先建图
    let mut graph: Vec<Vec<i32>> = vec![];
    for _i in 0..=n {
        graph.push(vec![]);
    }
    for i in 0..a.len() {
        graph[a[i] as usize].push(b[i]);
        graph[b[i] as usize].push(a[i]);
    }
    // 建图完毕
    // 根据题目描述，办公室一定是0号点
    // 所有员工一定是往0号点汇聚

    // a 号，dfn[a] == 0 没遍历过！
    // dfn[a] != 0 遍历过！
    let mut dfn: Vec<i32> = repeat(0).take((n + 1) as usize).collect();
    // a为头的树，一共有10个节点
    // size[a] = 0
    // size[a] = 10
    let mut size: Vec<i32> = repeat(0).take((n + 1) as usize).collect();
    // 所有居民要汇总吗？
    // a为头的树，所有的居民是要向a来汇聚
    // cost[a] : 所有的居民要向a来汇聚，总油量的耗费
    let mut cost: Vec<i32> = repeat(0).take((n + 1) as usize).collect();
    unsafe { CNT = 0 };
    dfs(&mut graph, 0, &mut dfn, &mut size, &mut cost);
    return cost[0];
}

// 图 ： graph
// 当前的头，原来的编号，不是dfn序号！ : cur
// 从cur开始，请遍历
// 遍历完成后，请把dfn[cur]填好！size[cur]填好！cost[cur]填好
fn dfs(
    graph: &mut Vec<Vec<i32>>,
    cur: i32,
    dfn: &mut Vec<i32>,
    size: &mut Vec<i32>,
    cost: &mut Vec<i32>,
) {
    unsafe {
        CNT += 1;
    }
    dfn[cur as usize] = unsafe { CNT };
    size[cur as usize] = 1;
    for next in graph[cur as usize].clone().iter() {
        if dfn[*next as usize] == 0 {
            dfs(graph, *next, dfn, size, cost);
            size[cur as usize] += size[*next as usize];
            cost[cur as usize] += cost[*next as usize];
            cost[cur as usize] += (size[*next as usize] + 4) / 5;
        }
    }
}

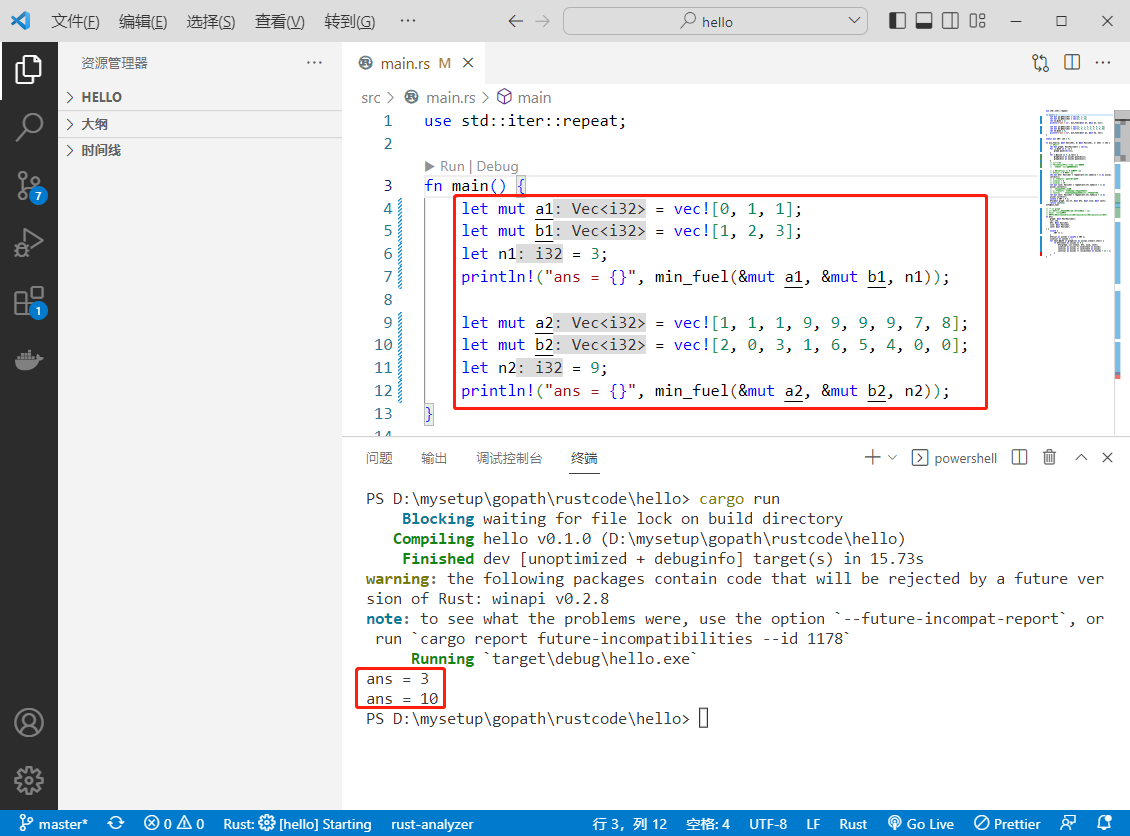
执行结果如下：

左神java代码