2022-08-08：给定一个数组arr，表示从早到晚，依次会出现的导弹的高度。 大炮打导弹的时候，如果一旦大炮定了某个高度去打，那么这个大炮每次打的高度都必须下降一点。 (1) 如果只有一个大炮，返回最多能拦截多少导弹。 (2) 如果所有的导弹都必须拦截，返回最少的大炮数量。

答案2022-08-08：

问题一：最长递减子序列。网上关于最长递增子序列的代码实在太多了，这里就不写了。 问题二：贪心+有序表。用已存在的最接近的稍高的大炮去打。

代码用rust编写。代码如下：

use std::collections::BTreeMap;
fn main() {
    let mut arr = vec![15, 7, 14, 6, 5, 13, 5, 10, 9];
    println!("ans = {}", num_of_cannon(&mut arr));
}

const MAX_VALUE: i32 = 1 << 31 - 1;

fn num_of_cannon(arr: &mut Vec<i32>) -> i32 {
    // key : 某个大炮打的结尾数值
    // value : 有多少个大炮有同样的结尾数值
    // 比如：
    // 一共有A、B、C三个大炮
    // 如果A大炮此时打的高度是17，B大炮此时打的高度是7，C大炮此时打的高度是13
    // 那么在表中：
    // 7, 1
    // 13, 1
    // 17, 1
    // 如果A大炮此时打的高度是13，B大炮此时打的高度是7，C大炮此时打的高度是13
    // 那么在表中：
    // 7, 1
    // 13, 2
    let mut ends: BTreeMap<i32, i32> = BTreeMap::new();
    for num in arr.iter() {
        if ends.range(num + 1..).take(1).last() == None {
            ends.insert(MAX_VALUE, 1);
        }
        let ceil_key = *ends.range(num + 1..).take(1).last().unwrap().0;
        let ceil_value = *ends.range(num + 1..).take(1).last().unwrap().1;
        if ceil_value > 1 {
            ends.insert(ceil_key, ceil_value - 1);
        } else {
            ends.remove(&ceil_key);
        }
        ends.insert(
            *num,
            match ends.get(num) {
                Option::Some(v) => v + 1,
                Option::None => 1,
            },
        );
    }
    let mut ans = 0;
    for (_, value) in ends.iter() {
        ans += *value;
    }
    return ans;
}

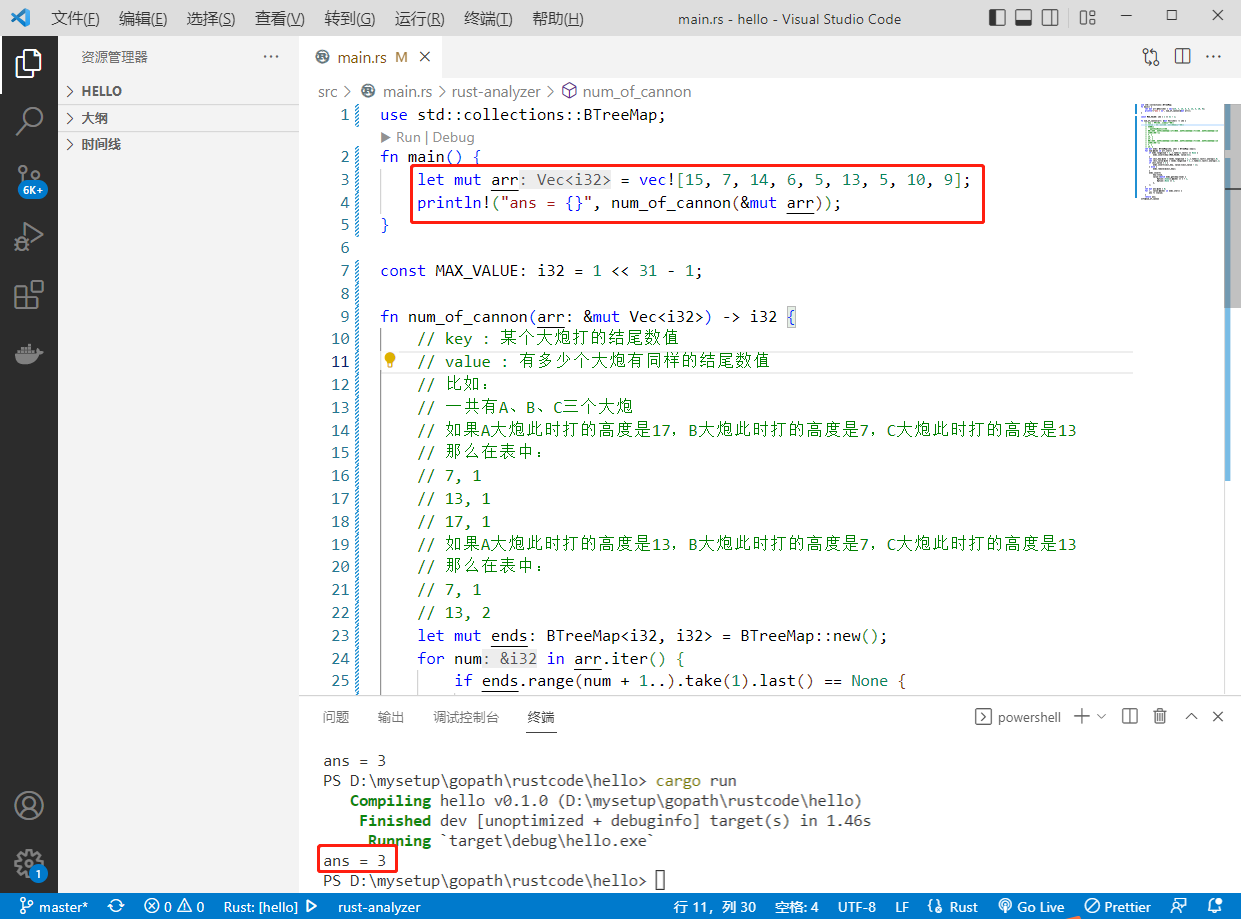
执行结果如下：

在这里插入图片描述

左神java代码