描述

题目描述

首先给定我们一个整数，然后问我们所有的连续序列的和等于这个整数，我们要把这些连续的序列输出出来

样例解释

样例输入

9

我们就是要找到，所有序列和为$99$的序列，序列长度至少为2，所以样例输出为

[[2,3,4],[4,5]]

题解

解法一：数学公式

实现思路

首先我们可以很轻松的知道，我们一个连续序列的和其实就是

(首项 + 末项) * 项数 / 2

那么我们可以推出如下等式

$\frac{(l+r)\ast (r-l+1)}{2}==n\backslash frac\{(l\; +\; r)\; *\; (r\; -\; l\; +\; 1)\}\{2\}\; ==\; n$

接下来移项可得

$(l+r)\ast (r-l+1)==2\ast n(l\; +\; r)\; *\; (r\; -\; l\; +\; 1)\; ==\; 2\; *\; n$

然后我们打开括号,我们假设我们的左端点已知,寻找满足条件的右端点,我们可得

$2\ast n+l^2-l==r^2+r2\; *n\; +\; l\; ^\; \{2\}\; -\; l\; ==\; r\; ^\; \{2\}\; +\; r$

然后我们即可根据这个式子写出代码,枚举所有的可能

代码实现

class Solution {
public:
    vector<vector<int> > FindContinuousSequence(int sum) {
        vector<vector<int>> res;
//         最后的答案数组
        for (int i = 1; i < sum; i++) {
//             遍历我们的开头
            vector<int> tmp;
//             临时数组
            for (int j = i; j < sum; j++) {
                tmp.push_back(j);
//                 每次都去放入临时数组
                if (j * j + j == 2 * sum + i * i - i) {
//                     如果满足了我们的数学公式，我们可以直接存到答案数组，然后跳出循环
                    res.push_back(tmp);
                    break;
                }
            }
        }
        return res;
    }
};

时空复杂度分析

时间复杂度: $O(n^2)O(n\; ^\; 2)$

理由如下:因为我们遍历了两层$forfor$循环,所以我们的时间复杂度就是$n^{2}n\; ^\; 2$的

空间复杂度: $O(1)O(1)$

理由如下: 我们定义的变量是为了储存最后的结果，我们不计算结果数组的空间

解法二：双指针

实现思路

首先我们可以维护我们的一个窗口，让窗口内的值的和最终要等于我们的要求的值，然后就会有一下几种操作

1. 如果窗口内的值比我们要求的和大，那么我们可以让慢指针向前移动，减少窗口内的值
2. 如果窗口内的值比我们要求的和小，那么我们可以让快指针向前移动，增大窗口内的值
3. 如果窗口内的值跟我们要求的和一样，那么我们可以把这个存到我们的答案数组中
4. 如果我们的慢指针的值已经比我们要求的值大了，那么我们可以直接结束循环了

代码实现

class Solution {
public:
    vector<vector<int> > FindContinuousSequence(int sum) {
        int l = 1, r = 1, num = 0;
//         左右指针
        vector<vector<int>> res;
//         最后的答案数组
        while (l <= r) {
//             双指针
            if (l >= sum) break;
//             如果越过了我们要求去的值，直接跳出循环
            if (num < sum) num += r, ++ r;
//             如果当前窗口的和比我们要的值小，我们快指针向后移动一位
            else if (num > sum) num -= l, ++ l;
//             如果当前窗口的和比我们的值要大，我们把慢指针向前移动一位
            else {
                vector<int> tmp;
                for (int i = l; i < r; i++) tmp.push_back(i);
                num -= l, ++ l;
                res.push_back(tmp);
//                 当满足条件的时候，把我们的当前这个窗口内的元素存起来
//                 然后放到我们的二维数组之中
            }
        }
        return res;
    }
};

图解代码

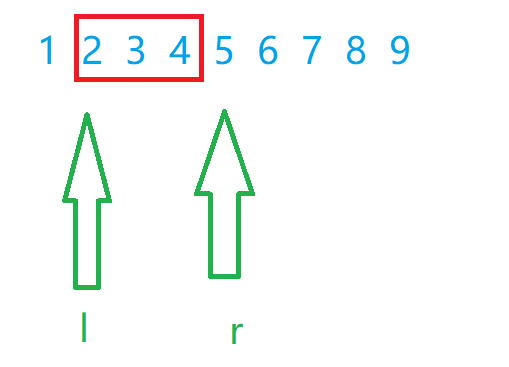
时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 我们只是简单的遍历一遍我们给定数的长度

空间复杂度: $O(1)O(1)$

理由如下: 我们除了最后的大难数组没有引用其他大的变量空间