题目大意
一个非递减的排序数组,从某个地方进行旋转,要找到原数组中最小的元素。
解法
几个月前写了一个题解,被其他同学找出了很多漏洞,当时考虑问题不够全面,另外牛客网上的测试用例也比较少,很多错误没有被发现,这次根据评论区的反馈,做了一个彻底的修改。
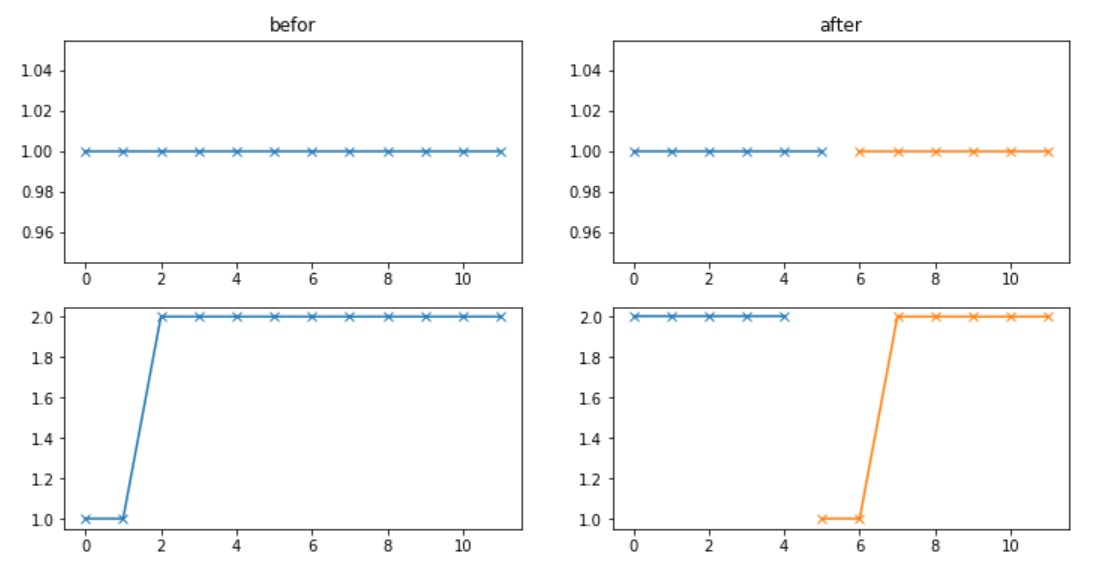
首先举两个例子,下图中左边两幅是非递减数组绘制的图像,右边是旋转后绘制的图像。可以看出,旋转后右侧一定是小于等于左侧的。原数组中最小的值,其实就是右半边的左端点。

既然是排序后的数组,虽然经过了旋转,但是直觉还是告诉我要使用二分查找。二分查找涉及到三个量 lo, hi,mid。我们的目标是找到右边部分的左端点。
如果 mid 落在左半边,那么 lo=mid+1,否则设置 hi=mid。这样不断缩小范围,最终就能找到这个最低点。
那么如何确定 mid 落在那边呢,由于左半边一定大于等于右半边,因此可以使用 nums[mid] 和左半段左端点比较,如果落在左半段,那么 nums[mid] >= nums[0]。但是落在右半段,也有可能 nums[mid] == nums[0] 啊,因为右侧的右端点可能和左侧左端点的值相同。
因此我们需要保证左半部分一定大于右半部分,为此,我们只需要做如下操作:
while(nums[lo] == nums.back()){
lo ++;
} 处理完成后,我们在 [lo,hi) 上寻找最小值。若 nums[mid] >= nums[lo] 那么 mid 落在左半部分,否则落在右侧。
经过一些朋友的提醒下,我发现还存在其他一些特殊情况:
特殊情况一:如果数组中所有元素的值都相同,那么 lo 就会一直增加,最终越界。
特殊情况二:如果左右两边相等的元素数量相同,那么循环完毕后 lo 就会是右半边的左端点。此时 [lo, hi) 所指的区间是递增区间,前面提到的二分查找策略此时就失效了。
下面是综合以上分析给出的解答:
class Solution {
public:
int minNumberInRotateArray(vector<int> nums) {
int lo = 0, hi = nums.size();
while(lo < hi && nums[lo] == nums.back()){
lo ++;
}
// 特殊情况一,所有元素都相等
if(lo == hi){
return nums[0];
}
// 特殊情况二
if(nums[lo] < nums.back()){
return nums[lo];
}
int left_min = nums[lo];
while(lo < hi){
int mid = lo + (hi - lo) / 2;
if(nums[mid] >= left_min){
lo = mid + 1;
}else{
hi = mid;
}
}
return nums[lo];
}
}; 



 京公网安备 11010502036488号
京公网安备 11010502036488号