codeforces#Round 604-E. Beautiful Mirrors(期望DP)
链接:
https://codeforces.com/contest/1265/problem/E
题意:

Examples
input
1
50
output
2
input
3
10 20 50
output
112
Note
In the first test, there is only one mirror and it tells, that Creatnx is beautiful with probability 1/2. So, the expected number of days until Creatnx becomes happy is 2.
有n个镜子,每个镜子有pi/100的概率回答是,初始从1开始,如果询问镜子回答为是,则下一天将询问第i+1个镜子,当第n个镜子回答是时,游戏结束。如果镜子回答为否,则下一天将重新访问第1个镜子。求游戏结束的期望步数。
思路:经典概率DP + 快速幂+费马定理+逆元:
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 998244353;
const int maxn = 2e5+10;
ll dp[maxn];
ll pow(ll a, ll b){
ll res=1;
while(b){
if(b&1){
res = (res*a) % mod;
}
a = (a*a) % mod;
b >>= 1;
}
return res;
}
int main(){
ios_base::sync_with_stdio(0);
int n;
cin >> n;
for(int i=1; i<=n; i++){
ll x;
cin >> x;
ll p = 100 * pow(x, mod-2) % mod;
dp[i] = (dp[i-1]+1)*p%mod;
}
cout << dp[n] << endl;
return 0;
}
知识点:
给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。例如26≡2(mod 12)。
,其中
为任意质数而
为与其互质的任意整数。
对于正整数
和
,如果有
,那么把这个同余方程中
的最小正整数解叫做
模
的逆元。
逆元一般用扩展欧几里得算法来求得,如果
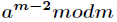
有关求逆元的方法,我在学习之后会更新(^ ^)。




 京公网安备 11010502036488号
京公网安备 11010502036488号