数据结构（十二）图的定义和实现

图

1. 什么是图

表示”多对多”的关系
包含
- 一组顶点：通常用 V（Vertex）表示顶点集合
- 一组边：通常用 E（Edge）表示边的集合
  - 边是顶点对：（v,w）∈ E，其中 v,w ∈ V v—w
  - 有向边 <v,w> 表示从 v 指向 w 的边（单行线） v→w
  - 不考虑重边和自回路

2. 常见术语

无向图：图中所有的边无所谓方向
有向图：图中的边可能是双向，也可能是单向的，方向是很重要的
权值：给图中每条边赋予的值，可能有各种各样的现实意义
网络：带权值的图
邻接点：有边直接相连的顶点
出度：从某顶点发出的边数
入度：指向某顶点的边数
稀疏图：顶点很多而边很少的图
稠密图：顶点多边也多的图
完全图：对于给定的一组顶点，顶点间都存在边

3. 抽象数据类型定义

类型名称：图（Graph）
数据对象集：G（V，E）由一个非空的有限顶点集合 V 和一个有限边集合 E 组成
操作集：对于任意图 G ∈ Graph，以及 v ∈ V，e ∈ E

主要操作有：
- Graph Crate()：建立并返回空图
- Graph InsertVertex(Graph G,Vertex v)：将 v 插入 G
- Graph InsertEdge(Graph G,Edge e)：将 e 插入 G
- void DFS(Graph G,Vertex v)：从顶点 v 出发深度优先遍历图 G
- void BFS(Graph G,Vertex v)：从顶点 v 出发宽度优先遍历图 G

1. 邻接矩阵表示

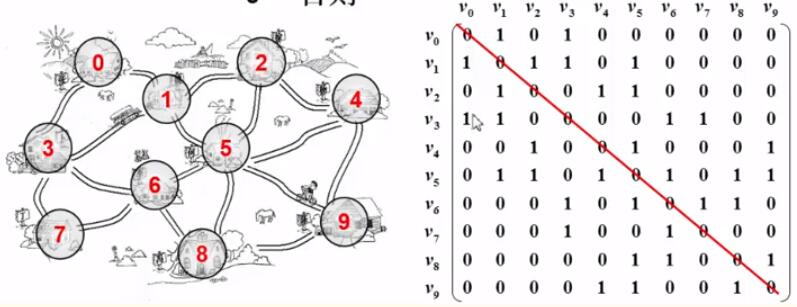
邻接矩阵 G $[N] [N]$ ——N 个顶点从 0 到 N-1 编号

$G [i] [j] = {\begin{matrix} <mstyle displaystyle="false" scriptlevel="0"> 1 </mstyle> & <mstyle displaystyle="false" scriptlevel="0"> 若 < v_{i}, v_{j} > 是 G 中的边 </mstyle> \\ <mstyle displaystyle="false" scriptlevel="0"> 0 </mstyle> & <mstyle displaystyle="false" scriptlevel="0"> 否则 </mstyle> \end{matrix}$
特征：
- 对角线元素全 0
- 关于对角线对称
优点：
- 直观、简单、好理解
- 方便检查任意一对顶点间是否存在边
- 方便找任一顶点的所有邻接点
- 方便计算任一顶点的度
  - 无向图：对应行（或列）非 0 元素的个数
  - 有向图：对应行非 0 元素的个数是出度；对应列非 0 元素的个数是入度
缺点：
- 浪费空间——存稀疏图
- 浪费时间——统计稀疏图的边

#include<stdio.h>
#include<stdlib.h>
#define MaxVertexNum 100
typedef int weightType;
typedef int Vertex;
typedef int DataType;
typedef struct GNode *ptrToGNode;
struct GNode{   // 图 
	int Nv;   // 顶点数 
	int Ne;   // 边数
	weightType G[MaxVertexNum][MaxVertexNum];
	DataType Data[MaxVertexNum]; // 存顶点的数据 
}; 
typedef ptrToGNode MGraph;
typedef struct ENode *ptrToENode;
struct ENode{  // 边 
	Vertex V1,V2;    // 有向边<V1,V2> 
	weightType Weight;  // 权重 
};
typedef ptrToENode Edge;

// 初始化图 
MGraph Create(int VertexNum){
	Vertex v,w;
	MGraph Graph;
	
	Graph = (MGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;
	Graph->Ne = 0;
	
	for(v=0;v<VertexNum;v++)
		for(w=0;w<VertexNum;w++)
			Graph->G[v][w] = 0;
	return Graph;
}

// 插入边 
MGraph Insert(MGraph Graph,Edge E){
	
	// 插入边 <V1,V2>
	Graph->G[E->V1][E->V2] = E->Weight;
	
	// 如果是无向图，还需要插入边 <V2,V1>
	Graph->G[E->V2][E->V1] = E->Weight;
	
} 

// 建图 
MGraph BuildGraph(){
	MGraph Graph;
	Edge E;
	Vertex V;
	int Nv,i;
	scanf("%d",&Nv);   // 读入顶点数 
	Graph = Create(Nv);
	scanf("%d",&(Graph->Ne));  // 读入边数 
	if(Graph->Ne != 0){   
		E = (Edge)malloc(sizeof(struct ENode));
		for(i=0;i<Graph->Ne;i++){
			scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);  // 读入每个边的数据 
			Insert(Graph,E);
		}
	}
	return Graph;
}

// 遍历图
void print(MGraph Graph){
	Vertex v,w;
	for(v=0;v<Graph->Nv;v++){
		for(w=0;w<Graph->Nv;w++)
			printf("%d ",Graph->G[v][w]);
		printf("\n");
	}
} 

int main(){
	MGraph Graph;
	Graph = BuildGraph();
	print(Graph);
	return 0;
}

简洁版

#include<stdio.h>
#include<stdlib.h>
#define MAXN 100
int G[MAXN][MAXN],Nv,Ne;

void BuildGraph(){
	int i,j,v1,v2,w;
	
	scanf("%d",&Nv);
	// 初始化图 
	for(i=0;i<Nv;i++) 
		for(j=0;j<Nv;j++)
			G[i][j] = 0;
	scanf("%d",&Ne);
	// 插入边 
	for(i=0;i<Ne;i++){
		scanf("%d %d %d",&v1,&v2,&w);
		G[v1][v2] = w;
		G[v2][v1] = w;
	}
}


// 遍历图
void print(){
	int i,j;
	for(i=0;i<Nv;i++){
		for(j=0;j<Nv;j++)
			printf("%d ",G[i][j]);
		printf("\n");
	}
} 

int main(){
	BuildGraph();
	print();
	return 0;
}

2. 邻接表表示

邻接表：G[N] 为指针数组，对应矩阵每行一个链表，只存非 0 元素
特点：
- 方便找任一顶点的所有邻接顶点
- 节省稀疏图的空间
  - 需要 N 个头指针 + 2E 个结点（每个结点至少 2 个域）
- 对于是否方便计算任一顶点的度
  - 无向图：方便
  - 有向图：只能计算出度
- 不方便检查任意一对顶点间是否存在边

#include<stdio.h>
#include<stdlib.h>
#define MaxVertexNum 100
typedef int Vertex; 
typedef int DataType; 
typedef int weightType;  

typedef struct ENode *ptrToENode;
struct ENode{  // 边 
	Vertex V1,V2;    // 有向边<V1,V2> 
	weightType Weight;  // 权重 
};
typedef ptrToENode Edge;

typedef struct AdjVNode *ptrToAdjVNode;
struct AdjVNode{  // 邻接表内元素 
	Vertex AdjV;  // 邻接点下标 
	weightType Weight;  // 权值 
	ptrToAdjVNode Next;  // 下一个 
};

typedef struct VNode{  // 邻接表头 
	ptrToAdjVNode FirstEdge;  // 存每个顶点指针
	DataType Data;  // 顶点数据 
}AdjList[MaxVertexNum];

typedef struct GNode *ptrToGNode;
struct GNode{  // 图 
	int Nv;  // 顶点
	int Ne;  // 边数 
	AdjList G; // 邻接表 
}; 
typedef ptrToGNode LGraph;

// 初始化 
LGraph create(int VertexNum){
	Vertex v,w;
	LGraph Graph;
	
	Graph = (LGraph)malloc(sizeof(struct GNode));
	Graph->Nv = VertexNum;  // 初始化边
	Graph->Ne = 0;   // 初始化点
	
	// 每条边的 FirstEdge 指向 NULL 
	for(v=0;v<Graph->Nv;v++)
		Graph->G[v].FirstEdge = NULL;
	return Graph;
}

// 插入一条边到邻接表的顶点指针之后 
void InsertEdge(LGraph Graph,Edge E){
	ptrToAdjVNode newNode; 
	
	/**************** 插入边<V1,V2> ******************/ 
	// 为 V2 建立新的结点 
	newNode = (ptrToAdjVNode)malloc(sizeof(struct AdjVNode));
	newNode->AdjV = E->V2;
	newNode->Weight = E->Weight;
	
	// 将 V2 插入到邻接表头 
	newNode->Next = Graph->G[E->V1].FirstEdge;
	Graph->G[E->V1].FirstEdge = newNode;
	
	/*************** 若为无向图，插入边<V2,V1> *************/ 
	newNode = (ptrToAdjVNode)malloc(sizeof(struct AdjVNode));
	newNode->AdjV = E->V1;
	newNode->Weight = E->Weight;
	
	newNode->Next = Graph->G[E->V2].FirstEdge;
	Graph->G[E->V2].FirstEdge = newNode;
} 

// 建图
LGraph BuildGraph(){
	LGraph Graph;
	Edge E;
	Vertex V;
	int Nv,i;
	scanf("%d",&Nv);
	Graph = create(Nv);
	scanf("%d",&(Graph->Ne));
	if(Graph->Ne != 0){
		for(i=0;i<Graph->Ne;i++){
			E = (Edge)malloc(sizeof(struct ENode));
			scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
			InsertEdge(Graph,E);
		}
	}
	return Graph;
} 

// 打印 
void print(LGraph Graph){
	Vertex v;
	ptrToAdjVNode tmp;
	for(v=0;v<Graph->Nv;v++){
		tmp = Graph->G[v].FirstEdge;
		printf("%d ",v);
		while(tmp){
			printf("%d ",tmp->AdjV);
			tmp = tmp->Next;
		}
		printf("\n");
	}
}

int main(){
	LGraph Graph;
	Graph = BuildGraph();
	print(Graph);
	return 0;
}

简化版

#include<stdio.h>
#include<stdlib.h>
#define MaxVertexNum 100
typedef struct AdjVNode *AdjList;
struct AdjVNode{
	int weight;  // 权值 
  	int adjv;   // 下标 
	AdjList next;  // 其后一个 
};
AdjList Graph[MaxVertexNum];
int Ne,Nv;

// 建图
void BuildGraph(){
	int i;
	int v1,v2,w;
	AdjList NewNode;
	scanf("%d",&Nv);
	for(i=0;i<Nv;i++){
		Graph[i] = (AdjList)malloc(sizeof(struct AdjVNode));
		Graph[i]->adjv = i;
		Graph[i]->next = NULL;
	}
	scanf("%d",&Ne);
	for(i=0;i<Ne;i++){
		scanf("%d %d %d",&v1,&v2,&w);
		NewNode = (AdjList)malloc(sizeof(struct AdjVNode));
		NewNode->adjv = v1;
		NewNode->weight = w;
		
		NewNode->next = Graph[v2]->next;
		Graph[v2]->next = NewNode;
		
		NewNode = (AdjList)malloc(sizeof(struct AdjVNode));
		NewNode->adjv = v2;
		NewNode->weight = w;
		
		NewNode->next = Graph[v1]->next;
		Graph[v1]->next = NewNode;
	}
} 

void print(){
	AdjList tmp;
	int i;
	for(i=0;i<Nv;i++){
		tmp = Graph[i];
		while(tmp){
			printf("%d ",tmp->adjv);
			tmp = tmp->next;
		}
		printf("\n");
	}
}

int main(){
	
	BuildGraph();
	print();
	return 0;
}