堆
1. 什么是堆
优先队列(priority Queue):特殊的"队列",取出元素的顺序是依照元素的优先级(关键字)大小,而不是元素进入队列的先后顺序,以完全二叉树存储
两个特性
-
结构性:用数组表示的完全二叉树
-
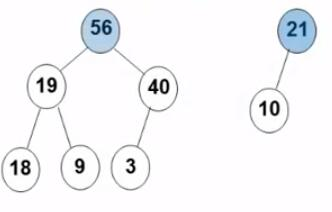
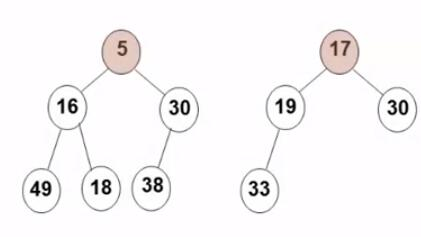
有序性:任一结点的关键字是其子树所有结点的最大值(或最小值)
-
“最大堆(MaxHeap)”,也称"大顶堆":最大值
-
“最小堆(MinHeap)”,也称"小顶堆":最小值
-
2. 堆的抽象数据类型描述
-
数据名称:最大堆(MaxHeap)
-
数据对象集:完全二叉树,每个结点的元素值不小于其子结点的元素值
-
操作集:最大堆 H ∈ MaxHeap,元素 item ∈ ElementType
主要操作有:
MaxHeap Create(int MaxSize):创建一个空的最大堆Boolean IsFull(MaxHeap H):判断最大堆 H 是否已满Boolean Insert(MaxHeap H,ElementType item):将元素 item 插入最大堆 HBoolean IsEmpty(MaxHeap H):判断最大堆 H 是否为空ElementType DeleteMax(MaxHeap H):返回 H 中最大元素(高优先级)
1. 插入
插入数组最后一个位置,再从下往上找合适地方
2. 删除
删除根结点,将数组最后一个位置的数取到根结点,从上往下找合适地方
#include<stdio.h>
#include<malloc.h>
#define MaxData 100000
#define ERROR -1
typedef int ElementType;
typedef struct HeapStruct *MaxHeap;
struct HeapStruct{
ElementType *Elements; // 存储堆元素的数组
int Size; // 堆的当前元素个数
int Capacity; // 堆的最大容量
};
MaxHeap Create(int MaxSize); // 建堆
bool IsFull(MaxHeap H); // 判断堆是否满
bool Insert(MaxHeap H,ElementType item); // 插入元素
bool IsEmpty(MaxHeap H); // 判断堆是否为空
ElementType DeleteMax(MaxHeap H); // 删除并返回堆中最大元素
void LevelOrderTraversal(MaxHeap H); // 层序遍历
// 建堆
MaxHeap Create(int MaxSize){
MaxHeap H = (MaxHeap)malloc(sizeof(struct HeapStruct));
// Elements[0] 作为哨兵,堆元素从 Elements[1] 开始存放
H->Elements = (ElementType *)malloc((MaxSize+1) * sizeof(ElementType));
H->Size = 0;
H->Capacity = MaxSize;
// "哨兵"大于堆中所有可能的值
H->Elements[0] = MaxData;
return H;
}
// 插入,从完全二叉树的最后一个位置插入
bool Insert(MaxHeap H,ElementType item){
if(IsFull(H)){
printf("堆已满,无法插入!\n");
return false;
}
int i = ++H->Size; // 指向堆中最后一个位置
for(;H->Elements[i/2] < item;i/=2) // 向上找比 item 大的结点
H->Elements[i] = H->Elements[i/2]; // 向下赋值
H->Elements[i] = item; // 找到了,把 item 值放进去
return true;
}
// 删除,从根结点删除
ElementType DeleteMax(MaxHeap H){
int parent,child;
ElementType Max,tmp;
if(IsEmpty(H)){
printf("堆为空,无法删除!\n");
return ERROR;
}
Max = H->Elements[1]; // 拿到最大值
tmp = H->Elements[H->Size--]; // 拿到完全二叉树最后一个值
// 判别条件:parent 是否有左孩子结点
for(parent=1;parent*2<=H->Size;parent=child){
// 左右孩子结点中找较大的值
child = 2 * parent; // 左孩子结点
// child!=H->Size 表示 child 不为当前最后一个结点,即 parent 有右孩子结点
if((child!=H->Size) &&(H->Elements[child] < H->Elements[child+1]))
child++;
// 给 tmp 找个合适的位置
// 如果当前左右孩子结点比 tmp 都小,说明 tmp 位置已经合适
if(H->Elements[child] <= tmp)
break;
else // 否则把较大的孩子结点提上来,自己继续下去找
H->Elements[parent] = H->Elements[child];
}
H->Elements[parent] = tmp; // 在合适的位置把 tmp 放进去
return Max;
}
// 判断是否已经满
bool IsFull(MaxHeap H){
return (H->Size == H->Capacity);
}
// 判断是否为空
bool IsEmpty(MaxHeap H){
return !H->Size;
}
// 层序遍历
void LevelOrderTraversal(MaxHeap H){
int i;
printf("层序遍历的结果是:");
for(i = 1;i<=H->Size;i++){
printf("%d ",H->Elements[i]);
}
printf("\n");
}
int main(){
MaxHeap H;
int MaxSize = 100;
H = Create(MaxSize);
Insert(H,55);
Insert(H,66);
Insert(H,44);
Insert(H,33);
Insert(H,11);
Insert(H,22);
Insert(H,88);
Insert(H,99);
/* 99 / \ 88 66 / \ / \ 55 11 22 44 / 33 */
LevelOrderTraversal(H);
DeleteMax(H);
LevelOrderTraversal(H);
DeleteMax(H);
LevelOrderTraversal(H);
DeleteMax(H);
LevelOrderTraversal(H);
DeleteMax(H);
LevelOrderTraversal(H);
return 0;
}
3. 最小堆的建立
不是初始化堆啦!
堆的建立:将已经存在的 N 个元素按最小堆的要求存放在一个一维数组中
0. 注意
对于一组相同数据,插入建堆和调整建堆建出来的堆也许不一样
1. 插入建堆
通过插入,将 N 个元素一个一个相继插入到一个初始为空的堆中去,其时间代价最大是 O(NlogN)(每次插入是 logN,总共 N 次)
#include<iostream>
#include<malloc.h>
const int MinData = -100000; // 哨兵值
const int MaxSize = 1005; // 最大个数
using namespace std;
typedef struct HeapStruct *Heap;
struct HeapStruct{
int *data; // 存值的数组
int size; // 当前元素个数
int capacity; // 最大容量
};
// 初始化堆
#include<iostream>
#include<malloc.h>
const int MinData = -100000; // 哨兵值
const int MaxSize = 1005; // 最大个数
using namespace std;
typedef struct HeapStruct *Heap;
struct HeapStruct{
int *data; // 存值的数组
int size; // 当前元素个数
int capacity; // 最大容量
};
// 初始化堆
Heap Create(){
Heap H;
H = (Heap)malloc(sizeof(struct HeapStruct));
H->data = (int *)malloc(sizeof(int) * (MaxSize+1));
H->size = 0;
H->capacity = MaxSize;
H->data[0] = MinData;
return H;
}
// 插入
void Insert(Heap H,int x){
int i = ++H->size; // 指向数组最后一个
for(;H->data[i/2]>x;i/=2)
H->data[i] = H->data[i/2];
H->data[i] = x;
}
// 遍历
void bl(Heap H){
for(int i=1;i<=H->size;i++)
cout<<H->data[i]<<" ";
}
int main(){
Heap H;
H = Create();
int n;
cin>>n;
for(int i=0;i<n;i++){
int t;
cin>>t;
Insert(H,t);
}
bl(H);
return 0;
}
2. 调整建堆
将 N 个元素直接按顺序存入,再调整各结点的位置(简单说来,对于从最后一个有孩子结点的结点来说,其本身结点和孩子结点共同构成"子最小堆",借助前面删除的想法,对每个"子最小堆"排序,当排序完成,整个最小堆也建立成功),时间代价是 O(n)
#include<iostream>
#include<malloc.h>
const int MinData = -100000; // 哨兵值
const int MaxSize = 1005; // 最大个数
using namespace std;
typedef struct HeapStruct *Heap;
struct HeapStruct{
int *data; // 存值的数组
int size; // 当前元素个数
int capacity; // 最大容量
};
// 初始化堆
Heap Create(){
Heap H;
H = (Heap)malloc(sizeof(struct HeapStruct));
H->data = (int *)malloc(sizeof(int) * (MaxSize+1));
H->size = 0;
H->capacity = MaxSize;
H->data[0] = MinData;
return H;
}
// 排序,类似堆的"删除操作"
void sort(Heap H,int i){
int child,parent;
int tmp = H->data[i]; // 拿到当前"根结点的值"
for(parent = i;parent*2<=H->size;parent = child){
child = 2 * parent;
if((child!=H->size) && (H->data[child+1] < H->data[child]))
child++;
if(H->data[child] >= tmp)
break;
else
H->data[parent] = H->data[child];
}
H->data[parent] = tmp;
}
// 调整
void adjust(Heap H){
int i= H->size/2;
for(;i>0;i--){
// 以每个有孩子结点的结点作为根结点,对其子树进行堆排序
sort(H,i);
}
}
// 遍历
void bl(Heap H){
for(int i=1;i<=H->size;i++){
cout<<H->data[i]<<" ";
}
cout<<endl;
}
int main(){
Heap H;
H = Create();
int n;
cin>>n;
for(int i=0;i<n;i++)
cin>>H->data[++H->size];
adjust(H);
bl(H);
return 0;
}






 京公网安备 11010502036488号
京公网安备 11010502036488号