错排问题比较难，但是也是经典算法问题
1 错排问题
家中阳台有10盆不同的花，为保持新鲜感，希望每天重新摆放，使得每盆花都不在第一天放的位置。那么最多可以保持多少天每天摆法都不同？
这是一个典型的错排问题。
错排的定义：若一个 n 元素的全排列中所有的元素都不在本来的位置上，那么称这个全排列就为原排列的一个错排（derangement） 。
也称作“伯努利-欧拉错装信封问题”（The Bernoulli-Euler problem of theMisaddressed letters） ——
- 小明给 n 个朋友写信，邀请他们来家中聚会，结果粗心的他却把请柬全都装错了信封。请问有多少种全部装错信封的情况
n 个元素的错排的个数记为 D(n)，下面通过两种计算方法来得到D（n）的值。
- 方法1：建立递推关系：
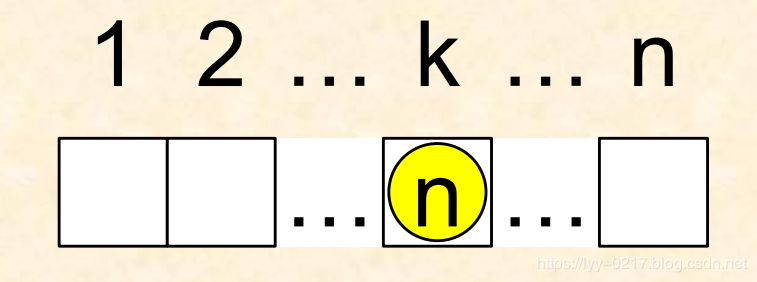
第1步，选择第 n 个元素的位置，共有n-1 种方法（假定放在编号为 k 的位置）；
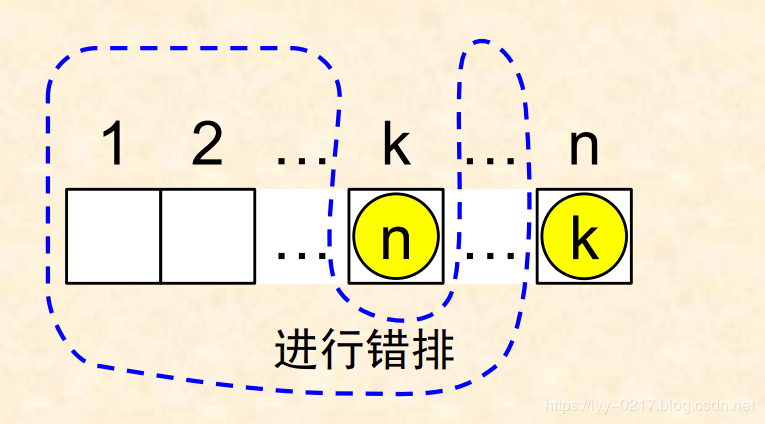
第2步，选择第 k 个元素的位置，有两种可能：
1）第 k 个元素放在编号为 n 的位置，此时剩下的n-2 个元素进行错排即可，方案数是 D(n-2)
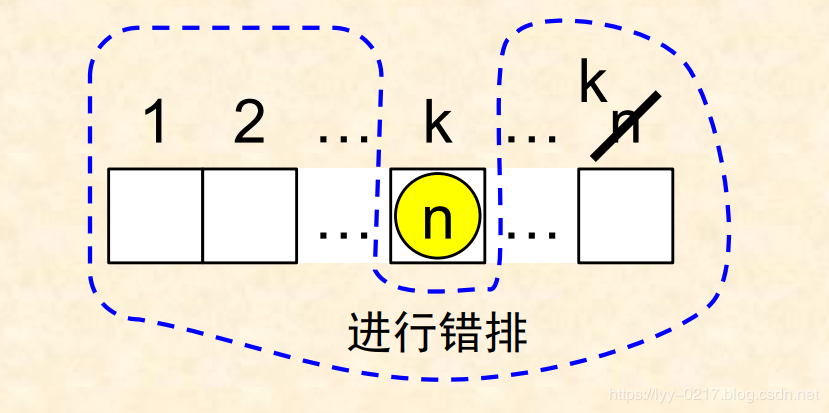
2）或者第 k 个元素不在编号为 n 的位置，此时把编号为 n 的位置视作编号为 k 的位置， 将 n-1 个元素进行错排即可， 方案数是 D(n-1)：
由此得到递推关系D(n)=(n-1)(D(n-2)+D(n-1))，这个足以写出递归代码。
很容易得到初值 D(1)=0 和 D(2)=1。
如果不使用递归，可以使用这个计算结果进行循环。
- 方法2 ：应用容斥原理
则D（n） = n! - | A 1 ∪A 2 ∪A 3 ∪...∪A n |
由容斥原理：
可得：
2 总结
- 学好数学
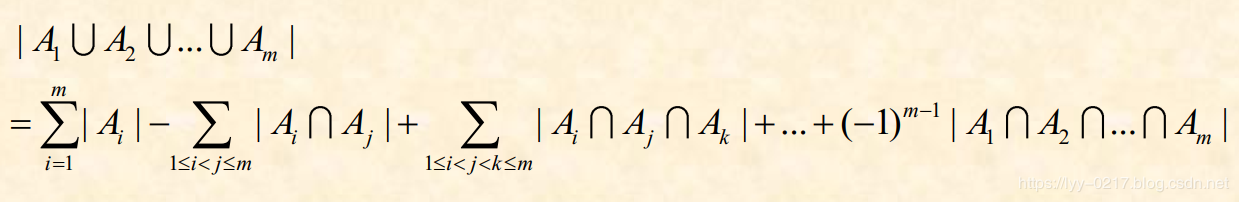
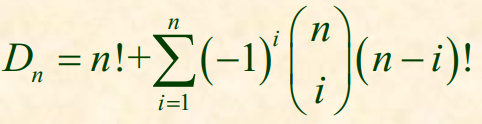
京公网安备 11010502036488号