拉格朗日介绍
先说说拉格朗日是啥吧
首先 拉格朗日插值是给你 n+1 个点 (x,y) 然后根据这n个点可以O(n^2)的求出多项式的系数。也就是解出这个多项式的答案。
假设给你一个多项式
y=a0+a1*x+a2*x^2
然后给你3个解 (x1,y1)(x2,y2)(x3,y3)你第一个想法是怎么解?解方程啊是不是
代进去是不是这样
解这个方程复杂度多少,高斯消元O(n^3)很显然复杂度高了。
拉格朗日就比较厉害了他能O(n^2)解决
首先 假设一个多项式
f1(x)=b+b1*x+b2*x^2
当然 x1 解是 1 x2 x3 解是 0
同理再假设 f2(x) f3(x)
然后L(x)=y1*f1(x)+y2*f2(x)+t3*f3(x) 这个就是最开始那个方程,不信?你把x1 x2 x3 带进去绝对是 y1 y2 y3
那么问题来了后面f1(x)这个多项式怎么求出来????
这就是拉格朗日基本公式
没错就是他
哦!搞错了是下面这个,上面那个是乘上yi的最终表达式
再来一遍,这就是拉格朗日基本公式
把这个多项式展开会发现非常神奇的事,当x=xj的时候刚好等于1 否则等于0
就是下面这样了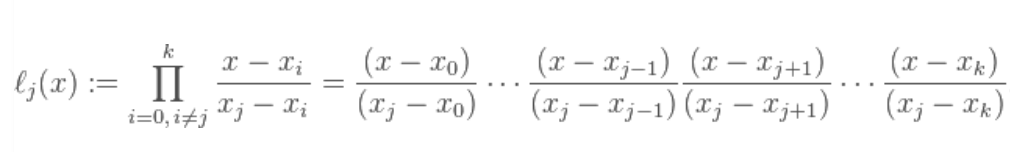
怕你还是看不懂,举个例子给你看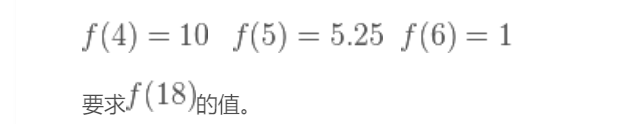


还有一个问题你们肯定很想问。。。知道公式之后怎么解。。。
对于这个问题
分母 是不是每次算一下就行了,答案是固定的
分子是不是一个大的多项式里面少了一个,就预处理出总的多项式然后,模拟除一下(x+c)的多项式
理论知识全部搞定,下面就给你贴模板了
板子
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
//这个是杜教的板子 我打了点注释
/// 注意mod,使用前须调用一次 polysum::init(int M);
/// 注意mod,使用前须调用一次 polysum::init(int M);
namespace polysum {
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
typedef long long ll;
const ll mod = 1e9 + 7; /// 取模值
ll powmod(ll a, ll b) {
ll res = 1;
a %= mod;
assert(b >= 0);
for (; b; b >>= 1) {
if (b & 1)res = res*a%mod;
a = a*a%mod;
}
return res;
}
const int D = 1010000; /// 最高次限制
ll a[D], f[D], g[D], p[D], p1[D], p2[D], b[D], h[D][2], C[D];
ll calcn(int d, ll *a, ll n) { //根据前 d 项 求 第n项
if (n <= d) return a[n];
p1[0] = p2[0] = 1;
rep(i, 0, d + 1) {
ll t = (n - i + mod) % mod;
p1[i + 1] = p1[i] * t%mod;
}
rep(i, 0, d + 1) {
ll t = (n - d + i + mod) % mod;
p2[i + 1] = p2[i] * t%mod;
}
ll ans = 0;
rep(i, 0, d + 1) {
ll t = g[i] * g[d - i] % mod*p1[i] % mod*p2[d - i] % mod*a[i] % mod;
if ((d - i) & 1) ans = (ans - t + mod) % mod;
else ans = (ans + t) % mod;
}
return ans;
}
void init(int M) { /// M:最高次
f[0] = f[1] = g[0] = g[1] = 1;
rep(i, 2, M + 5) f[i] = f[i - 1] * i%mod;
g[M + 4] = powmod(f[M + 4], mod - 2);
per(i, 1, M + 4) g[i] = g[i + 1] * (i + 1) % mod; //逆元
}
ll polysum(ll n, ll *arr, ll m) { /// a[0].. a[m] \sum_{i=0}^{n-1} a[i]
for (int i = 0; i <= m; i++)
a[i] = arr[i];
a[m + 1] = calcn(m, a, m + 1);
rep(i, 1, m + 2) a[i] = (a[i - 1] + a[i]) % mod;
return calcn(m + 1, a, n - 1);
}
ll qpolysum(ll R, ll n, ll *a, ll m) { /// a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i
if (R == 1) return polysum(n, a, m);
a[m + 1] = calcn(m, a, m + 1);
ll r = powmod(R, mod - 2), p3 = 0, p4 = 0, c, ans;
h[0][0] = 0;
h[0][1] = 1;
rep(i, 1, m + 2) {
h[i][0] = (h[i - 1][0] + a[i - 1])*r%mod;
h[i][1] = h[i - 1][1] * r%mod;
}
rep(i, 0, m + 2) {
ll t = g[i] * g[m + 1 - i] % mod;
if (i & 1) p3 = ((p3 - h[i][0] * t) % mod + mod) % mod, p4 = ((p4 - h[i][1] * t) % mod + mod) % mod;
else p3 = (p3 + h[i][0] * t) % mod, p4 = (p4 + h[i][1] * t) % mod;
}
c = powmod(p4, mod - 2)*(mod - p3) % mod;
rep(i, 0, m + 2) h[i][0] = (h[i][0] + h[i][1] * c) % mod;
rep(i, 0, m + 2) C[i] = h[i][0];
ans = (calcn(m, C, n)*powmod(R, n) - c) % mod;
if (ans<0) ans += mod;
return ans;
}
}
|
然后下面这个是求多项式的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
LL temp[maxn];
void mul(LL *f, int len, LL t) { //len为多项式的次数+1,函数让多项式f变成f*(x+t)
for(int i = len; i > 0; --i) {
temp[i] = f[i];
f[i] = f[i-1];
}
temp[0] = f[0], f[0] = 0;
for(int i = 0; i <= len; ++i) {
f[i] = (f[i] + t*temp[i])%mod;
}
}
void dev(LL *f, LL *r, LL t,int len) { //f是被除多项式的系数,r保存f除以x+t的结果 len是最高次项
for(int i = 0; i <= len; ++i) {
temp[i] = f[i];
}
for(int i = len; i > 0; --i) {
r[i-1] = temp[i];
temp[i-1] = (temp[i-1] - t*temp[i])%mod;
}
return;
}
LL a[maxn], b[maxn], c[maxn];
LL x[maxn], y[maxn]; //x,y输入从 1开始到n
int n;
void lglr() {
memset(a,0,sizeof a);
b[1] = 1, b[0] = -x[1];
for(int i = 2; i <= n; ++i) {
mul(b, i, -x[i]);
}//预处理(x-x1)*(x-x2)...*(x-xn)
for(int i = 1; i <= n; ++i) {
LL fz = 1;
for(int j = 1; j <= n; ++j) {
if(j == i) continue;
fz = fz*(x[i] - x[j])%mod;
}
fz = qm(fz, mod-2);
fz = fz*y[i]%mod;//得到多项式系数
dev(b, c, -x[i],n);//得到多项式,保存在b数组
for(int j = 0; j < n; ++j) a[j] = (a[j] + fz*c[j])%mod;
}
}
LL cal(LL k) { //计算第x=k值
LL ans = 0;
LL res = 1;
for(int i = 0; i < n; ++i) {
ans = (ans + res*a[i])%mod;
res = res*k%mod;
}
ans = (ans + mod)%mod;
return ans;
}
|




 京公网安备 11010502036488号
京公网安备 11010502036488号