题意:
二维平面的第一象限内,有两种操作,一是在某个点的权值加一,二是查询一个直角梯形范围内的权值的和。
题解:
std解法是CDQ分治,想了个分块暴力的方法,速度竟然是最快的。。。
将整个第一象限分为128*128(1<<7)个块,每个块是边长为(1<<23)的正方形,这样可以表示坐标(1<<30)范围内的点,满足题目给出的范围
建立一个128*128的二维树状数组,用来求一个矩形区域内的权值的和
对于第一种操作,求出点所在的块,在二维树状数组中单点修改就行
关键是第二种操作
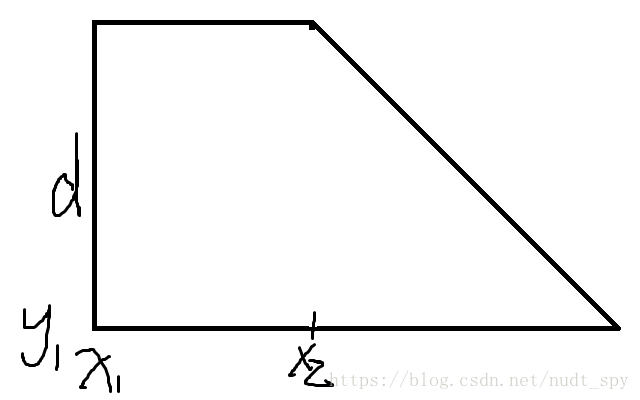
一个直角梯形:
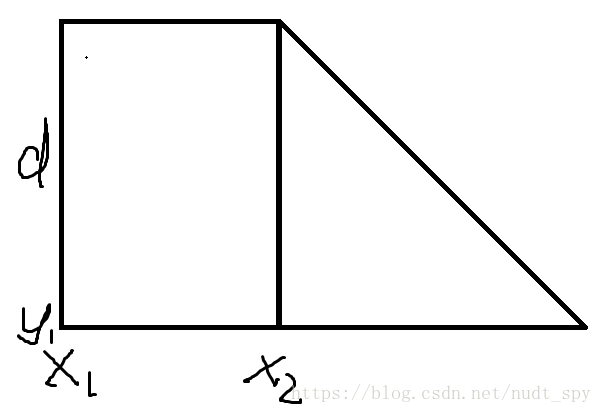
分解为:
矩形和直角三角形分开计算
矩形部分:
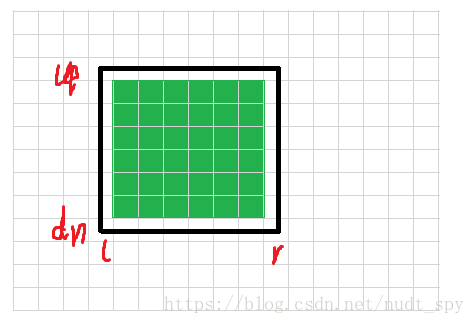
先确定矩形的边界占据的块,即求出矩形所在块的x方向和y方向的范围:l , r , dn , up
那么,范围 l+1 ~ r-1 , dn+1 ~ up -1 内的块中的点一定是在矩形范围内的,就是下图中的绿色部分
绿色部分的权值和用二维树状数组解决,4条边界所经过的块就必须要遍历一遍,对于每一个块,看块中包含的点在矩形内的个数,两部分加一起就是矩形范围内的权值和
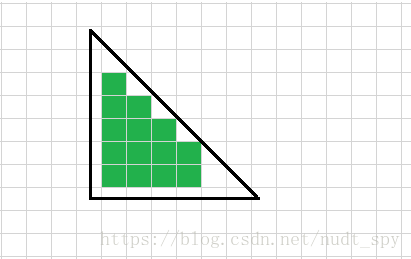
然后是三角形部分
由于不是矩形,无法通过二维树状数组一次求解,方法是遍历左右区间,即 x 方向在 [ l+1 , r-1 ] ,y方向为 dn+1 的块,就是绿色块的底边,通过直线方程可以计算出当前列的绿色块的上限,显然每一列的个数是不同的,这样一列一列计算出绿色块包含的权值和(这里由于是一列,所以可以用一维树状数组求解),再遍历边界经过的块,两部分加一起就是三角形范围内的权值和
具体实现起来方法很多,不同方法需要考虑的细节不一样,下面的方法需要考虑的细节比较少。
复杂度分析
最坏1e5个点,1e4多个块,由于数据随机,平均一个块不到10个点
操作一复杂度为二维树状数组复杂度:log*log,即7*7
操作二复杂度
矩形:一个二维树状数组查询:log*log,边界经过的块的期望值为128个,每个块平均有10个点,总复杂度为128*10
三角形:边界经过的块的期望值为128个,求绿色块时每一列查询一次一维树状数组,单次为log,共128*7,边界复杂度同矩形,为128*10,总复杂度为128*10
所以,操作二复杂度为128*10
由于操作一二是随机出现,实际复杂度远远达不到上限,原因:首先前期每个块中点的个数远达不到10,后期个数可能会多一点,但这一定是操作一过多导致的,这又导致操作二变得很少,于是发现真正耗时间的操作二少很多。一次操作姑且期望为 1e3,共有1e5个操作,总用时1e8
代码:
#include<bits/stdc++.h>
#define N 100010
#define INF 0x3f3f3f3f
#define eps 1e-10
#define pi 3.141592653589793
#define mod 998244353
#define LL long long
#define pb push_back
#define cl clear
#define si size
#define lb lower_bound
#define ub upper_bound
#define mem(x) memset(x,0,sizeof x)
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
using namespace std;
struct Point
{
int x,y;
};
vector<Point> a[1<<7][1<<7];
int dd[1<<7][1<<7],f[1<<7][1<<7],op,x,y,xx,d;
inline void update(int x,int y)
{
for (int i=x;i<128;i|=(i+1))
for (int j=y;j<128;j|=(j+1))
dd[i][j]++;
for (int i=y;i<128;i|=(i+1))
f[x][i]++;
}
inline int sum(int x,int y)
{
int res=0;
for (int i=x;i>=0;i=(i&(i+1))-1)
for (int j=y;j>=0;j=(j&(j+1))-1)
res+=dd[i][j];
return res;
}
inline int gsum(int x,int y)
{
int res=0;
for (int i=y;i>=0;i=(i&(i+1))-1)
res+=f[x][i];
return res;
}
inline int spyer(int l,int r,int dn,int up) //矩形
{
if (r>127) r=127;
if (up>127) up=127;
int res=0,t=xx+d+y;
for (int i=l;i<=r;i++)
{
for (int j=0;j<a[i][up].size();j++) //上边界
{
int tx=a[i][up][j].x,ty=a[i][up][j].y;
if (tx>=x && tx<=xx && ty<=y+d && ty>=y) res++;else
if (tx>xx && tx<=xx+d && ty>=y && tx+ty<=t) res++;
}
if (dn<up)
for (int j=0;j<a[i][dn].size();j++) //下边界
{
int tx=a[i][dn][j].x,ty=a[i][dn][j].y;
if (tx>=x && tx<=xx && ty>=y && ty<=y+d) res++;else
if (tx>xx && tx<=xx+d && ty>=y && tx+ty<=t) res++;
}
}
for (int i=dn+1;i<up;i++)
{
for (int j=0;j<a[l][i].size();j++) //左边界
{
int tx=a[l][i][j].x,ty=a[l][i][j].y;
if (tx>=x && tx<=xx && ty>=y && ty<=y+d) res++;else
if (tx>xx && tx<=xx+d && ty>=y && tx+ty<=t) res++;
}
if (l<r)
for (int j=0;j<a[r][i].size();j++) //右边界
{
int tx=a[r][i][j].x,ty=a[r][i][j].y;
if (tx>=x && tx<=xx && ty>=y && ty<=y+d) res++;else
if (tx>xx && tx<=xx+d && ty>=y && tx+ty<=t) res++;
}
}
l++;r--;dn++;up--;
if (l>r || dn>up) return res;else
return res+sum(r,up)-sum(l-1,up)-sum(r,dn-1)+sum(l-1,dn-1);
}
inline int spyerr() // 三角形
{
int res=0;
int nx=((xx>>23)+1)<<23,t=xx+d+y; //三角形的左边界在矩形上其实已经算过了,重新确定需要计算的左边界,一定是某一个块的起始位置
xx+=d;
if (nx>xx) return 0;
if ((nx>>23)>127) return 0;
int l=nx>>23,r=xx>>23,dn=y>>23;
for (int i=l;i<=r;i++) // 计算下边界
{
for (int j=0;j<a[i][dn].size();j++)
{
int tx=a[i][dn][j].x,ty=a[i][dn][j].y;
if (tx>=nx && tx<=xx && ty>=y && tx+ty<=t) res++;
}
}
int ny=(dn+1)<<23; y=t-nx; //重新确定需要计算的下边界,一定是某一个块的起始位置
xx=t-ny; r=xx>>23;
if (ny>y) return res;
for (int i=l;i<=r;i++)
{
int tx=i<<23,ttx=((i+1)<<23)-1,ty=t-tx,tty=t-ttx,t1=ty>>23,t2=tty>>23; //当前列的块的坐标左右边界所处的块为t1,t2
if (t1<128) for (int j=0;j<a[i][t1].size();j++) // 斜边经过的块的计算
{
int tx=a[i][t1][j].x,ty=a[i][t1][j].y;
if (tx>=nx && tx<=xx && ty>=ny && tx+ty<=t) res++;
}
if (t2!=t1 && t2>dn && t2<128)
for (int j=0;j<a[i][t2].size();j++) // 斜边经过的块的计算
{
int tx=a[i][t2][j].x,ty=a[i][t2][j].y;
if (tx>=nx && tx<=xx && ty>=ny && tx+ty<=t) res++;
}
if (t2>127) t2=128;
if (t2-1>dn)res+=gsum(i,t2-1)-gsum(i,dn); //绿色的块计算
}
return res;
}
int main()
{
int n;
sc(n);
for (int i=1;i<=n;i++)
{
sc(op);
if (op==1)
{
scc(x,y);
a[x>>23][y>>23].pb(Point{x,y});
update(x>>23,y>>23);
}else
{
scc(x,y); scc(xx,d);
int tmp=spyer(x>>23,xx>>23,y>>23,(y+d)>>23);
tmp+=spyerr();
printf("%d\n",tmp);
}
}
}







 京公网安备 11010502036488号
京公网安备 11010502036488号