
闲聊
感觉这场Div3比以往的都要有难度,感觉跟Div2差不多了要,依稀记得之前觉得Div3还是能AK的,现在做E都感觉比较吃力了,这次D还因为一个点没想通wa了几发
题解部分
给定一个01串s,然后有n个字符串t,第i个字符串t分别是s复制过来之后将第i个字符反转,即将0变为1,将1变为0,问你这n个字符串总共有多少个1
算一遍就好,还是挺好算的
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
void solve() {
init();
int n;
cin>>n;
string s;
cin>>s;
int num1=0,num2=0;
for(int i=0;i<n;i++) {
if(s[i]=='1') num1++;
else num2++;
}
cout<<(n - 1 ) * num1 + num2<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}
B.St. Chroma
给定一个n和一个x,要求构造一个0-n-1的排列,使得根据前i个数的mex值组成的数组中,x出现次数最大
涉及mex值的一般贪心就好,本题也是一样,只要贪心,要让mex值达到x,然后再尽可能让mex值不变就好,所以我们首先从0到x-1,然后把比x大的数输出一遍,最后输出x即可
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
void solve() {
init();
int n,x;
cin>>n>>x;
for(int i=0;i<x;i++) cout<<i<<" ";
for(int i=n-1;i>=x;i--) cout<<i<<" ";
cout<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}
先给定n和x,然后给定一个长度为n的数组a和数组b,其中数组b有些数字丢失了(表示为 b i b_i bi = -1),问你有多少个数组b使得对于所有的i, b i b_i bi ≥0 并且 b i b_i bi≤x,并且 a i a_i ai + b i b_i bi 的值是相等的。
很简单,如果已经b数组已经有一部分数字,那么我们只要检查有无冲突便可,如果有冲突就是-1,如果没有冲突就是1。
至于b数组里的数字全部丢失的情况,我们想象一个数组平移的过程,在这个平移过程中,保证最小值大于等于0,保证最大值小于等于k便可,那么有多少个我们是可以直接计算得到的
(这边提倡自己推公式看看捏)
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
int b[N];
void solve() {
init();
int sign = 1;
int num = -1;
int n,k;
cin>>n>>k;
int minvalue = MOD;
int maxvalue = 0;
for(int i=1;i<=n;i++) cin>>a[i],minvalue = min(minvalue,a[i]),
maxvalue =max(maxvalue,a[i]);
for(int i=1;i<=n;i++) {
cin>>b[i];
//cout<<a[i]<<" "<<b[i]<<" "<<num<<"\n";
if(b[i]!=-1) {
if(num == -1) {
num = a[i] + b[i];
}
else {
if(a[i] + b[i] != num) {
sign = 0;
}
}
}
}
if(!sign) {
cout<<0<<"\n";
return ;
}
//cout<<"num:"<<num<<"\n";
if(num != -1) {
for(int i=1;i<=n;i++) {
if(num - a[i] < 0 || num - a[i] > k) {
cout<<0<<"\n";
return;
}
}
}
if(num != -1) {
cout<<1<<"\n";
}
else cout<<k - (maxvalue - minvalue) + 1<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}
D. Flower Boy
给定一个长度为n的数组a,一个长度为m的数组b,对a数组从左到右看,如果a数组里面的数字满足当前b数组第一个数字,那么拿走a数组当前数字以及b数组的第一个数字。现在能进行一次操作在任何位置插入一个任何值x,问你这个x最小是多少能够保证b数组里的所有数都能拿走,如果无论怎么操作都拿不走b数组所有数字,则输出-1,如果不需要操作就能拿完b数组里的所有数,那么就输出0
分析一下:如果遍历一遍发现不用操作也能拿完那就直接输出就好
如果需要操作,就想想我们肯定是让操作***来的数字和b数组某个位置对应,然后让a数组后面的数字和b数字后面的数字匹配
所以能想到一个暴力的做法:遍历b数组里的所有数字,表示操作***来的数字和b数组第i个数匹配,然后再遍历检查a数组后面的数字和b数字后面的数字,看是否能拿完b数组的所有数字
但是这种做法肯定是超时了的,所以我们就想想该如何优化,其实有经验的应该早就想到了,能够优化的就是遍历检查的这部分,应该优化成能够直接查询知道后面这部分是否能拿完b数组的所有数
所以我们可以开一个后缀数组,从后往前对a数组和b数组进行匹配检查,并且记录第i个数字能和b数组从后往前能拿b数组从后往前多少个数字
那我们还可以开一个前缀数组,从前往后对a数组和b数组进行同样的操作。最后我们遍历位置,查询哪个位置能够满足插入一个数字之后能够拿完b数组里的所有数字的,如果有那就记录最小值,如果没有就输出-1
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
int b[N];
int pre[N];
int bac[N];
void solve() {
init();
int sign = 0;
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int j=1;j<=m;j++) cin>>b[j];
for(int i=1;i<=n;i++) {
pre[i] = pre[i-1];
if(pre[i] < m && a[i] >= b[pre[i] + 1]) pre[i]++;
//cout<<i<<" "<<pre[i]<<"\n";
}
if(pre[n] == m) {
cout<<0<<"\n";
return ;
}
bac[n + 1] = 0;
for(int i=n;i>=1;i--) {
bac[i] = bac[i + 1];
if(bac[i] < m && a[i] >= b[m - bac[i]]) bac[i]++;
//cout<<i<<" "<<bac[i]<<"\n";
}
int minvalue = MOD;
for(int i=1;i<=n+1;i++) {
if(pre[i-1] + bac[i] + 1 >= m) {
sign = 1;
minvalue = min(minvalue,b[pre[i-1] + 1]);
}
}
if(sign) cout<<minvalue<<"\n";
else cout<<-1<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}
给定n和q,然后给定一个长度为n的排列。在接下来q次查询中,每次查询给定l,r,k.然后会在[l,r]范围进行二分操作,二分操作详情如下:
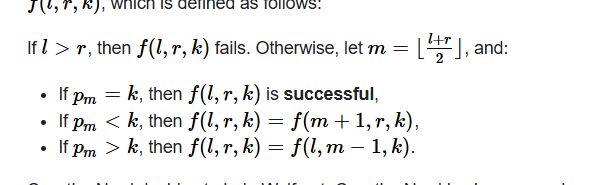
由于p排列并不一定是排好序的,所以有可能二分操作找不到想要的数字,但是你可以选择d个非目标数字(d的大小由自己定),然后对其任意排序。问你d的大小最小为多少能够让该二分操作能够找到下想要的数字
那我们只要记录每个数字的位置,然后跟着二分的过程贪心就好了。具体来讲就是如果目标数字在右边,那么我们这里就需要一个比目标数字小的数字,反之同理
记录额外需要比目标数字小的位置个数,以及额外需要比目标数字大的位置个数,那么我们要移走全部,选定的肯定是这两个数字的最大值乘2
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
int b[N];
int pos[N];
void solve() {
init();
int n,q;
cin>>n>>q;
for(int i=1;i<=n;i++) {
cin>>a[i];
pos[a[i]] = i;
}
while(q--) {
int l,r,k;
cin>>l>>r>>k;
if(pos[k] < l || pos[k] > r) {
cout<<-1<<" ";
continue;
}
int havebig=0,havesmall=0;
int needbig=0,needsmall=0;
while(l < r) {
int mid = (l + r) >>1;
if(pos[k] == mid) break;
if(pos[k] > mid) {
if(a[mid] < k) havesmall++;
else needsmall++;
l = mid + 1;
}
else {
if(a[mid] > k) havebig++;
else needbig++;
r = mid - 1;
}
}
//cout<<"\n"<<havebig<<" "<<needbig<<" "<<havesmall<<" "<<needsmall<<":";
if(havebig + needbig > n - k || havesmall + needsmall > k - 1) cout<<-1<<" ";
else cout<<max(needbig,needsmall) * 2<<" ";
}
cout<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}




 京公网安备 11010502036488号
京公网安备 11010502036488号