2022-06-20：一个二维矩阵，上面只有 0 和 1，只能上下左右移动， 如果移动前后的元素值相同，则耗费 1

2022-06-20：一个二维矩阵，上面只有 0 和 1，只能上下左右移动， 如果移动前后的元素值相同，则耗费 1 ，否则耗费 2。 问从左上到右下的最小耗费。 来自网易。3.27笔试。

答案2022-06-20：

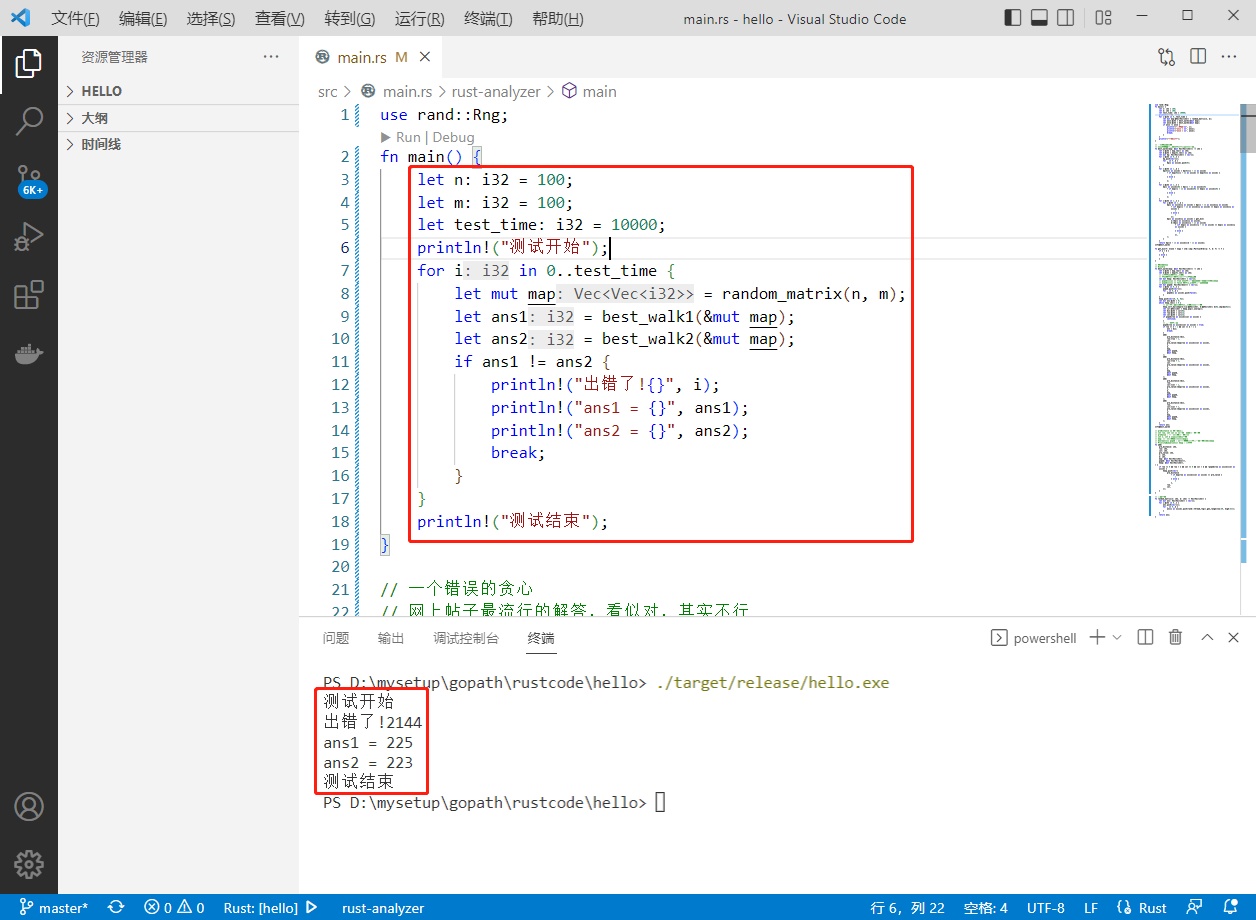
1.网上非常流行的方法，但这是错误的。这道题动态规划是做不了的。因为上下左右四个方向都可能走，而不是右下两个方向。 2.要用dijskra+小根堆才能实现。 代码里1和2两种方法都实现了，运行结果可以证明方法1是错误的。

代码用rust编写。代码如下：

use rand::Rng;
fn main() {
    let n: i32 = 100;
    let m: i32 = 100;
    let test_time: i32 = 10000;
    println!("测试开始");
    for i in 0..test_time {
        let mut map = random_matrix(n, m);
        let ans1 = best_walk1(&mut map);
        let ans2 = best_walk2(&mut map);
        if ans1 != ans2 {
            println!("出错了!{}", i);
            println!("ans1 = {}", ans1);
            println!("ans2 = {}", ans2);
            break;
        }
    }
    println!("测试结束");
}

// 一个错误的贪心
// 网上帖子最流行的解答，看似对，其实不行
fn best_walk1(map: &mut Vec<Vec<i32>>) -> i32 {
    let n = map.len() as i32;
    let m = map[0].len() as i32;
    let mut dp: Vec<Vec<i32>> = vec![];
    for i in 0..n {
        dp.push(vec![]);
        for _ in 0..m {
            dp[i as usize].push(0);
        }
    }
    for i in 1..m {
        dp[0][i as usize] = dp[0][(i - 1) as usize]
            + if map[0][(i - 1) as usize] == map[0][i as usize] {
                1
            } else {
                2
            };
    }
    for i in 1..n {
        dp[i as usize][0] = dp[(i - 1) as usize][0]
            + if map[(i - 1) as usize][0] == map[i as usize][0] {
                1
            } else {
                2
            };
    }
    for i in 1..n {
        for j in 1..m {
            dp[i as usize][j as usize] = dp[(i - 1) as usize][j as usize]
                + (if map[(i - 1) as usize][j as usize] == map[i as usize][j as usize] {
                    1
                } else {
                    2
                });
            dp[i as usize][j as usize] = get_min(
                dp[i as usize][j as usize],
                dp[i as usize][(j - 1) as usize]
                    + (if map[i as usize][(j - 1) as usize] == map[i as usize][j as usize] {
                        1
                    } else {
                        2
                    }),
            );
        }
    }
    return dp[(n - 1) as usize][(m - 1) as usize];
}

fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a < b {
        a
    } else {
        b
    }
}

// 正确的解法
// Dijskra
fn best_walk2(map: &mut Vec<Vec<i32>>) -> i32 {
    let n = map.len() as i32;
    let m = map[0].len() as i32;
    // 小根堆：[代价，行，列]
    // 根据代价，谁代价小，谁放在堆的上面
    let mut heap: Vec<Vec<i32>> = vec![];
    // poped[i][j] == true 已经弹出过了！不要再处理，直接忽略！
    // poped[i][j] == false 之间(i,j)没弹出过！要处理
    let mut poped: Vec<Vec<bool>> = vec![];
    for i in 0..n {
        poped.push(vec![]);
        for _ in 0..m {
            poped[i as usize].push(false);
        }
    }
    heap.push(vec![0, 0, 0]);
    let mut ans = 0;
    while heap.len() > 0 {
        // 当前弹出了，[代价，行，列]，当前位置
        heap.sort_by(|a, b| b[0].cmp(&a[0]));
        let cur = heap.pop().unwrap();
        let dis = cur[0];
        let row = cur[1];
        let col = cur[2];
        if poped[row as usize][col as usize] {
            continue;
        }
        // 第一次弹出！
        poped[row as usize][col as usize] = true;
        if row == n - 1 && col == m - 1 {
            ans = dis;
            break;
        }
        add(
            dis,
            row - 1,
            col,
            map[row as usize][col as usize],
            n,
            m,
            map,
            &mut poped,
            &mut heap,
        );
        add(
            dis,
            row + 1,
            col,
            map[row as usize][col as usize],
            n,
            m,
            map,
            &mut poped,
            &mut heap,
        );
        add(
            dis,
            row,
            col - 1,
            map[row as usize][col as usize],
            n,
            m,
            map,
            &mut poped,
            &mut heap,
        );
        add(
            dis,
            row,
            col + 1,
            map[row as usize][col as usize],
            n,
            m,
            map,
            &mut poped,
            &mut heap,
        );
    }
    return ans;
}

// preDistance ： 之前的距离
// int row, int col ： 当前要加入的是什么位置
// preValue : 前一个格子是什么值，
// int n, int m ：边界，固定参数
// map: 每一个格子的值，都在map里
// boolean[][] poped : 当前位置如果是弹出过的位置，要忽略！
// PriorityQueue<int[]> heap : 小根堆
fn add(
    pre_distance: i32,
    row: i32,
    col: i32,
    pre_value: i32,
    n: i32,
    m: i32,
    map: &mut Vec<Vec<i32>>,
    poped: &mut Vec<Vec<bool>>,
    heap: &mut Vec<Vec<i32>>,
) {
    if row >= 0 && row < n && col >= 0 && col < m && !poped[row as usize][col as usize] {
        heap.push(vec![
            pre_distance
                + if map[row as usize][col as usize] == pre_value {
                    1
                } else {
                    2
                },
            row,
            col,
        ]);
    }
}

// 为了测试
fn random_matrix(n: i32, m: i32) -> Vec<Vec<i32>> {
    let mut ans: Vec<Vec<i32>> = vec![];
    for i in 0..n {
        ans.push(vec![]);
        for _ in 0..m {
            ans[i as usize].push(rand::thread_rng().gen_range(0, 2));
        }
    }
    return ans;
}

执行结果如下：

左神java代码