描述
题目描述
给定我们一个正整数是类型的, 然后让我们求最多会有多少个连续的
题解
解法一: 暴力枚举所有的情况
实现思路
首先我们可以开辟一个临时数组, 然后我们每次都是去把我们二进制的最后一位存储进去, 然后我们暴力遍历一次这个数组来寻找我们的最大值, 然后这里我们还有另一种方法就是使用我们的的这个容器, 可以节省空间和时间, 这个可以看我在牛客的另一篇题解 bitset传送门
代码实现
#include <bits/stdc++.h>
using namespace std;
signed main() {
int n;
while (cin >> n) {
vector<int> a;
while (n) {
a.emplace_back(n & 1);
n >>= 1;
}
// 把我们输入的这个数字的二进制存入到我们的数组里面
int maxx = 0, tmp = 0;
// 我们定义一个我们的最大的连续的1的数量是maxx
// 然后我们的tmp是我们的每次临时的
for (auto &it : a) {
if (it == 1) {
tmp += 1;
maxx = max(maxx, tmp);
} else {
tmp = 0;
}
// 如果当前的这位是我们的1的这个位置
// 那么我们值加加
// 否则我们清空临时存储的tmp
}
cout << maxx << "\n";
}
return 0;
}
时空复杂度分析
时间复杂度 :
理由如下: 我们每次把我们最后的一位存储到我们的数组中, 总共会进行次操作, 所以我们的时间复杂度是
空间复杂度 :
理由如下: 因为我们开辟了一个大小为的大小的数组来存储我们的这个每一位二进制
解法二
实现思路
我们考虑如何对我们的做法一进行一个优化, 我们考虑有没有什么操作是不必要的, 我们可以很容易的发现这么的一个问题, 就是我们的这个开辟的数组似乎只是起到一个辅助存储的作用, 那么我们可不可以考虑我们把这个数组优化掉, 我们在我们直接在缩短的过程中进行判断
图解代码

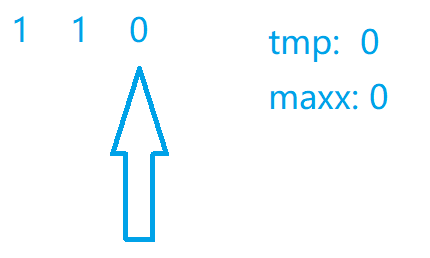
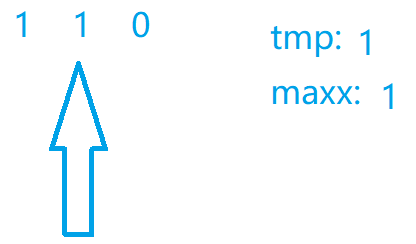

代码实现
#include <bits/stdc++.h>
using namespace std;
signed main() {
int n;
while (cin >> n) {
int maxx = 0, tmp = 0;
// maxx存储最后的最多的1的数量
// tmp存储的我们临时的1的数量
while (n) {
if (n & 1) {
tmp += 1;
maxx = max(maxx, tmp);
// 如果我们当前的位置是1, 那么我们tmp增加一个, 时刻更新最大值
} else {
tmp = 0;
// 如果是0的话, 那么我们就把我们现在的这个临时存储变成0
}
n >>= 1;
// 我们把最后已经判断完的那一位删掉
}
cout << maxx << "\n";
}
return 0;
}
时空复杂度分析
时间复杂度 :
理由如下: 我们把我们当前的这个的所有二进制位遍历之后, 我们会发现我们一共是要进行次的操作
空间复杂度 :
理由如下: 因为我们只引入了常数级别的空间






 京公网安备 11010502036488号
京公网安备 11010502036488号