u1,u2,u3分别是不同坐标系的三个坐标,
h1,h2,h3就是拉梅系数
①直角坐标:
u1=x u2=y u3=z
h1=h2=h3=1
②圆柱坐标:
u1=ρ,u2=ϕ,u3=z
h1=1,h2=ρ,h3=1
③球坐标:( ϕ是2π那个角)
u1=r,u2=θ,u3=ϕ
h1=1,h2=r,h3=rsinθ
然后就有一个统一的矢量场公式:
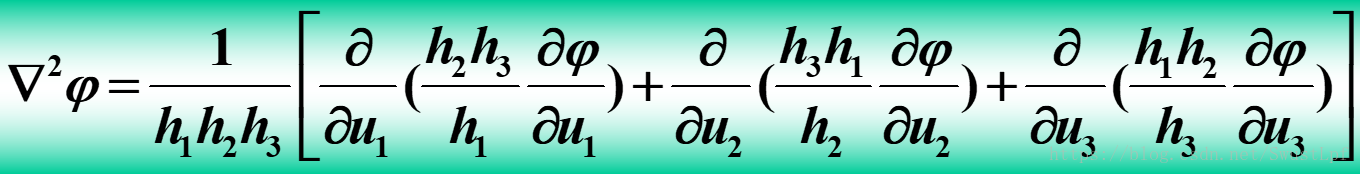

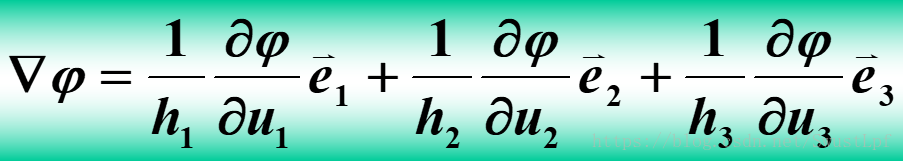

雅克比行列式
以前只在线性代数中听过这个,但是高数中也有一个
比如 dxdy=rdrdθ怎么来的哇?
以前只能用画图来解释,没想到竟然有变换的公式,一直都想有,以为没有,结果真的有。。。
⎩⎨⎧x=x(u,v)y=y(u,v)
J=∣∣∣∣∣∣∂u∂x∂u∂y∂v∂x∂v∂y∣∣∣∣∣∣
dxdy=∣J∣⋅dudv
有了这个公式就知道极坐标这个怎么来的了
⎩⎨⎧x=rcosθy=rsinθ
J=∣∣∣∣∣∣∂r∂x∂r∂y∂θ∂x∂θ∂y∣∣∣∣∣∣=∣∣∣∣∣∣cosθsinθ−rsinθrcosθ∣∣∣∣∣∣=r(cos2θ+sin2θ)=r
∴dxdy=r⋅drdθ



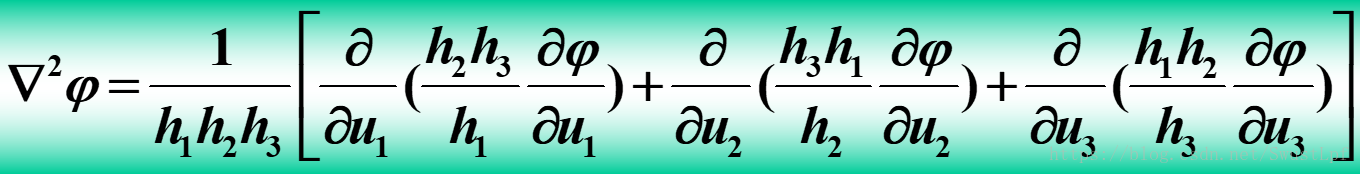

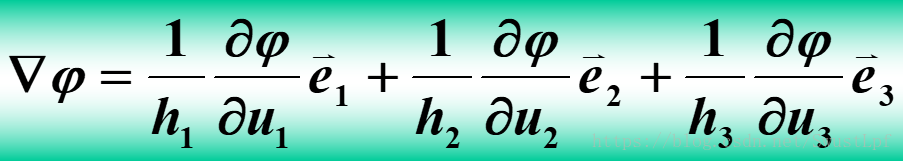


 京公网安备 11010502036488号
京公网安备 11010502036488号