描述

题目描述

给定我们一个序列, 让我们求取最长的上升子序列, 如果有相同的, 我们返回我们字典序最小的那一个

题解

解法一: 动态规划TLE

实现思路:

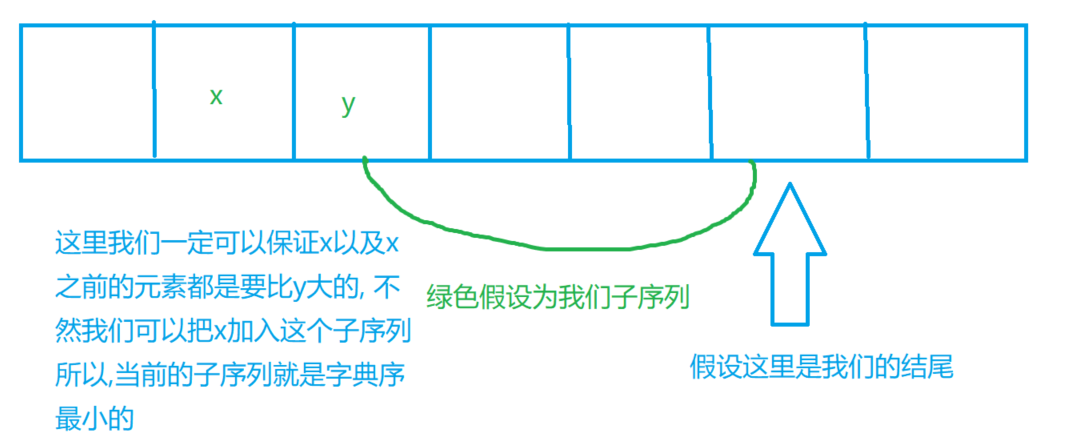
我们可以直接套用最长上升子序列的模板, 求取出我们的最长的值, 然后我们去倒序查找, 这里简单解释一下倒序查找的一个问题, 我们从后往前找, 可以保证这么样的一个问题, 就是我们的最后一定是某一段子序列的结尾, 那么我们从结尾向前找, 这样找到的一定是子序列的字典序最小的, 这个是为什么呢? 我们可以假设找到了某一段子序列的开头, 如果这个位置的前面还有比这个位置更小的元素, 那么我们现在的这个子序列就不是我们当前的最长上升子序列的, 所以我们想要找到最长的子序列, 那么我们可以保证在同样长度下, 这个子序列的开头字典序一定是最小的

首先我们先定义我们的DPDP数组的含义: 我们定义dp[i]dp[i]为考虑前ii个元素, 以第ii个元素结尾的最长上升子序列的长度, 此时我们的arr[i]arr[i]必须被选取

然后我们推我们状态转移方程:

首先我们在计算dp[i]dp[i]之前, 我们已经是计算出来了dp[0...i−1]dp[0 ... i - 1]的值

那么如果我们0<=j<=i并且arr[i]>arr[j]0 <= j <= i 并且 arr[i] > arr[j] 那么我们的状态转移方程为:

dp[i]=max(dp[j])+1dp[i] = max(dp[j]) + 1

这里我们考虑我们这个ii之前的所有数, 如果可以满足当前的arr[i]arr[i]比我们之前的某一个数大, 那么我们可以把arr[i]arr[i]放到那个序列的后面, 所以这样递推之后, 我们最长上升子序列的长度就是我们dpdp数组的最大值

然后保证字典序最小, 我们就是可以从后向前找, 根据我们上面的解释

如图所示

20220212033318

代码实现

class Solution {
   public:
    vector<int> LIS(vector<int>& arr) {
        int len = arr.size();
        if (len == 0) return {};
//         如果数组为空的话，我们直接返回空
        vector<int> dp(len, 0);
        for (int i = 0; i < len; i++) {
            dp[i] = 1;
            for (int j = 0; j < i; j++)
                if (arr[j] < arr[i]) dp[i] = max(dp[i], dp[j] + 1);
        }
//         这个是求取最长上升子序列的模板
        int maxx = *max_element(dp.begin(), dp.end());
//         获取我们的最大长度
        vector<int> res(maxx);
        for (int i = len - 1, j = maxx; i >= 0; i--) 
            if (dp[i] == j) j--, res[j] = arr[i];
//         转移到我们的答案数组中
        return res;
    }
};

时空复杂度分析

时间复杂度: O(n2)O(n ^ 2)

理由如下: 我们求取最长上升子序列是两次循环

空间复杂度: O(n)O(n)

理由如下: 开辟了一个dpdp数组

解法二: 二分

实现思路

这里其实就是存在一个简单的贪心问题, 如果我们想要这个上升子序列尽可能的长, 那么我们就要让他上升的慢, 所以我们希望每次在上升子序列最后加的数尽可能的小

那么我们就可以维护一个数组, 用于表示我们长度为ii的最长上升子序列的末尾元素的最小值, 这样我们是可以保证我们的这个数组是一个随着长度的递增在单调上升的一个数组, 这样就满足了我们二分的一个条件

然后总体的算法流程就是:

  1. 我们遍历原来的序列, 假设我们遍历到了第ii位

如果我们当前这位比我们当前的维护的数组的最后一个元素的值小的话, 插入数组, 更新最大长度

否则的话, 我们直接在我们维护的数组中二分找到第一个比我们当前这个数小的数字, 然后更新

20220212034439

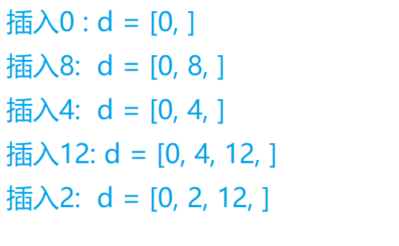
20220212034619

代码实现

class Solution {
   public:
    vector<int> LIS(vector<int>& arr) {
        if (arr.size() == 0) return {};
        vector<int> d, dp;
        // d是我们上面讲的辅助数组, dp是我们每一位最长多少
        d.emplace_back(arr[0]);
        dp.emplace_back(1);
        for (int i = 1; i < arr.size(); i++) {
            // 这步就是我们上面讲的第一个步骤, 如果比我们最后一个元素大, 直接插入
            if (arr[i] > d.back()) d.emplace_back(arr[i]), dp.emplace_back(d.size());
            else {
                int pos = lower_bound(d.begin(), d.end(), arr[i]) - d.begin();
                d[pos] = arr[i];
                dp.emplace_back(pos + 1);
                // 二分找到第一个小于等于当前的这个数字的
            }
        }
        vector<int> res(d.size());
        for (int i = dp.size() - 1, j = d.size(); j; i--)
            if (dp[i] == j) j--, res[j] = arr[i];
        return res;
        // 这里就是我们上面讲的逆序的过程, 这样保证字典序最小
    }
};

时空复杂度分析

时间复杂度: O(nlogn)O(nlogn)

理由如下: 遍历一次数组, 遍历的过程最坏每次二分查找带一个loglog

空间复杂度: O(n)O(n)

理由如下: 开辟了一个dpdp和dd辅助数组