参考博客[https://blog.csdn.net/sacredness/article/details/93124338]，讲得比较清楚。

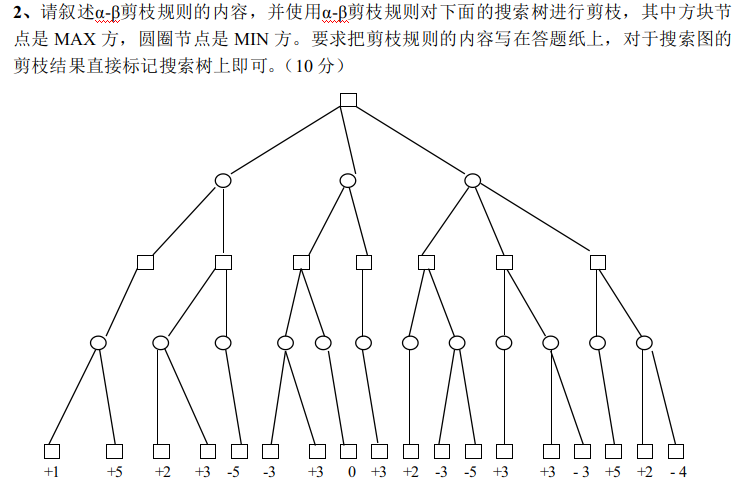
image.png

因为懒得再画图，所以所有节点以第几层(从上往下，最上面为第1层)第几个节点(从左往右)代替。

已知条件：

  • 矩形表示我方，想要数字最大化，圆形代表对方，想要数字最小化，叶子节点是已知的收益节点。

整个步骤：

  • 最底层是收益已知的点，所以从倒数第二层开始，从左往右，首先是第一个圆形节点，是对方的点，要取min，所以该点目前的范围就是小于等于1，因为该点另外一个儿子如果大于1，那对方肯定选左边的1，如果小于1，那肯定选这个小于1的，所以总的范围是小于等于1。
  • 再看该点的右儿子，5大于1，所以该点的值可以确定为1。
  • 所以该点的父节点，也就是第三层的第一个节点，目前的范围是大于等于1，因为是我方节点，要取max。
  • 然后，因为该矩形节点只有一个儿子，所以确定了范围也就确定了值，即第三层第一个节点的值可以确定为1，其父节点目前的范围是小于等于1。
  • 从左往右，再看倒数第二层的第二个圆形节点，同理，可以确定其值为2，那么他的父节点，也就是第三层的第二个节点，可以确定范围是大于等于2,。
  • 重点来了，第三层第二个节点范围确定是大于等于2，而他的父节点即第二层第一个节点确定范围是小于等于1，交集大小小于等于1，所以将第三层第二个节点的其他还没搜索的儿子全部剪枝掉。
  • 剩下的道理相同，就是时刻要注意看父节点的范围是不是已经确定了，看是否可以剪枝。