实习+秋招刷题019-020（牛客刷题）剑指offer

019重建二叉树
题目描述

给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。
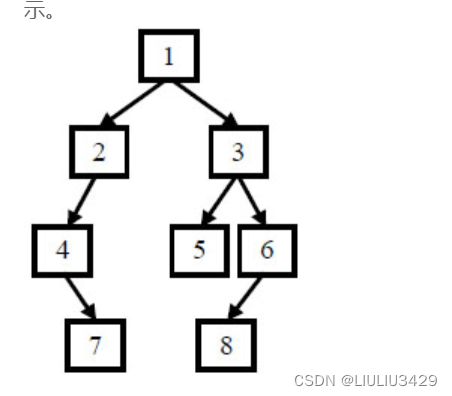
例如输入前序遍历序列{
   1,2,4,7,3,5,6,8}和中序遍历序列{
   4,7,2,1,5,3,8,6}，则重建出如下图所示。

关键解题思路
前序遍历：根左右； 中序遍历：左根右
递归：终止条件、返回值、本级任务
前序遍历找到根节点，在根据中序遍历划分左右子树，使用递归进行这个过程就可以建树。
注意：使用Arrays.copyofRange(原数组，左界限，有界限（不包含）)。
Solution

import java.util.*;

/* * public class TreeNode { * int val = 0; * TreeNode left = null; * TreeNode right = null; * public TreeNode(int val) { * this.val = val; * } * } */

public class Solution {
   
    /** * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可 * * * @param preOrder int整型一维数组 * @param vinOrder int整型一维数组 * @return TreeNode类 */
    public TreeNode reConstructBinaryTree (int[] preOrder, int[] vinOrder) {
   
        // write code here
        //递归：终止条件、返回值，本级任务
        //preorder的第一个值为头节点的值
        if(preOrder.length==0){
   
            return null;
        }
        if(preOrder.length==1){
   
            return new TreeNode(preOrder[0]);
        }
        int prenodeval = preOrder[0];
        TreeNode treenode= new TreeNode(prenodeval);
        int j=0;
        for(; j<vinOrder.length;j++){
   
            if(vinOrder[j]==prenodeval){
   
                break;
            }
        }
        treenode.left = reConstructBinaryTree(Arrays.copyOfRange(preOrder,1,j+1), Arrays.copyOfRange(vinOrder,0,j));
        treenode.right= reConstructBinaryTree(Arrays.copyOfRange(preOrder,j+1,preOrder.length), Arrays.copyOfRange(vinOrder,j+1,vinOrder.length));
        return treenode;
    }
}

020二叉树的下一个结点
题目描述

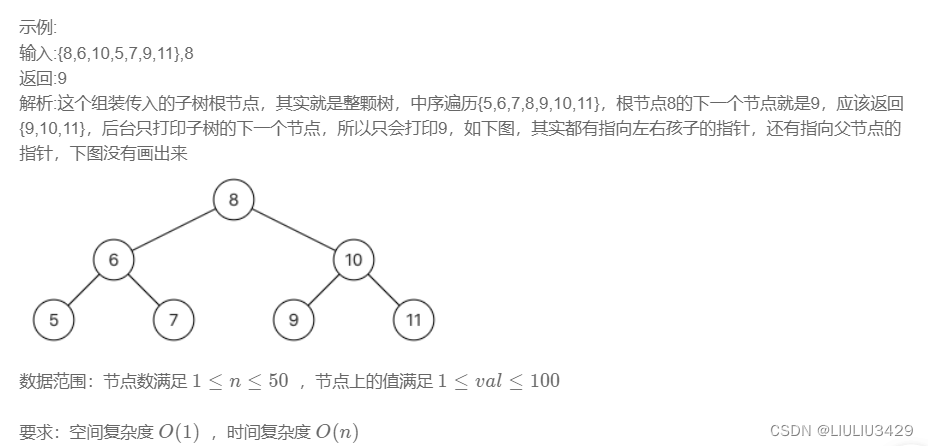
给定一个二叉树其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的next指针。下图为一棵有9个节点的二叉树。树中从父节点指向子节点的指针用实线表示，从子节点指向父节点的用虚线表示

关键解题思路
1、使用next找到根节点
2、递归，得到二叉树的中序遍历
3、根据2得到的中序遍历获得匹配的节点
Solution

import java.util.*;
/* public class TreeLinkNode { int val; TreeLinkNode left = null; TreeLinkNode right = null; TreeLinkNode next = null; TreeLinkNode(int val) { this.val = val; } } */
public class Solution {
   
    ArrayList<TreeLinkNode> nodes = new ArrayList<>(); 
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
   
        //1、找到根节点
        //2、递归，得到二叉树的中序遍历
        //3、根据中序遍历顺序，找到匹配的节点
       TreeLinkNode root =pNode;
       while(root.next!=null){
   
            root = root.next;
       }
       Order(root);
       for(int i=0;i<nodes.size()-1; i++){
   
            if(nodes.get(i)==pNode){
   
                return nodes.get(i+1);
            }
       }
        return null ;
        
    }
    void Order(TreeLinkNode root){
   
        if(root!=null){
   
            Order(root.left);
            nodes.add(root);
            Order(root.right);
        }
    }
}