文章目录

hdu 1010——tempter of the bone

一、问题描述

​ 一个迷宫有NxM格，有一些格子是地板，能走；有一些各自是障碍，不能走。给一个起点S和一个重点D。一只小狗从S出发，每步走一块地板，在每块地板不能停留，而且走过的地板都不能再走。给定一个T。问小狗能正好走T步到达D吗？

​ 输入：有很多测试样例。每个测试中，第一行输入整数N,M,T（1<N,M<7,0<T<50）。后面N行中，每行输入M个字符，有这些字符可以输入：‘X’:墙；‘S’:起点；‘D’:终点；‘.’:地板。最后一行输入’0 0 0’。表示输入结束。

​ 输出：每个测试，如果狗能到达，输出YES,否则输出NO。

二、剪枝

1.用到的变量名和含义

​ 1.k：表示已经走了多少步

​ 2.T：表示总共能走多少步

​ 3.f：曼哈顿距离——理论上的最短距离——f=abs(c-x)+abs(d-y);

2.可行性剪枝

​ 从题目中我们可以发现可行性剪枝的方法：一共走T步，现在走了K步，还要走X步，这时候要判断是否还可以走X步

​ （1）k+f>T——》f>T-k——当前位置到终点的要走的步数比从当前位置到终点要走的最小步数还要小，说明走不到了，直接剪掉。

3.奇偶剪枝

​ 奇偶剪枝其实很好理解：我们可以把这些个地板块以及墙等等组合成的区域看做是一个二维的网格区域，网格中的数只包含0，1两个数，并且他们是交错排布的，例如：

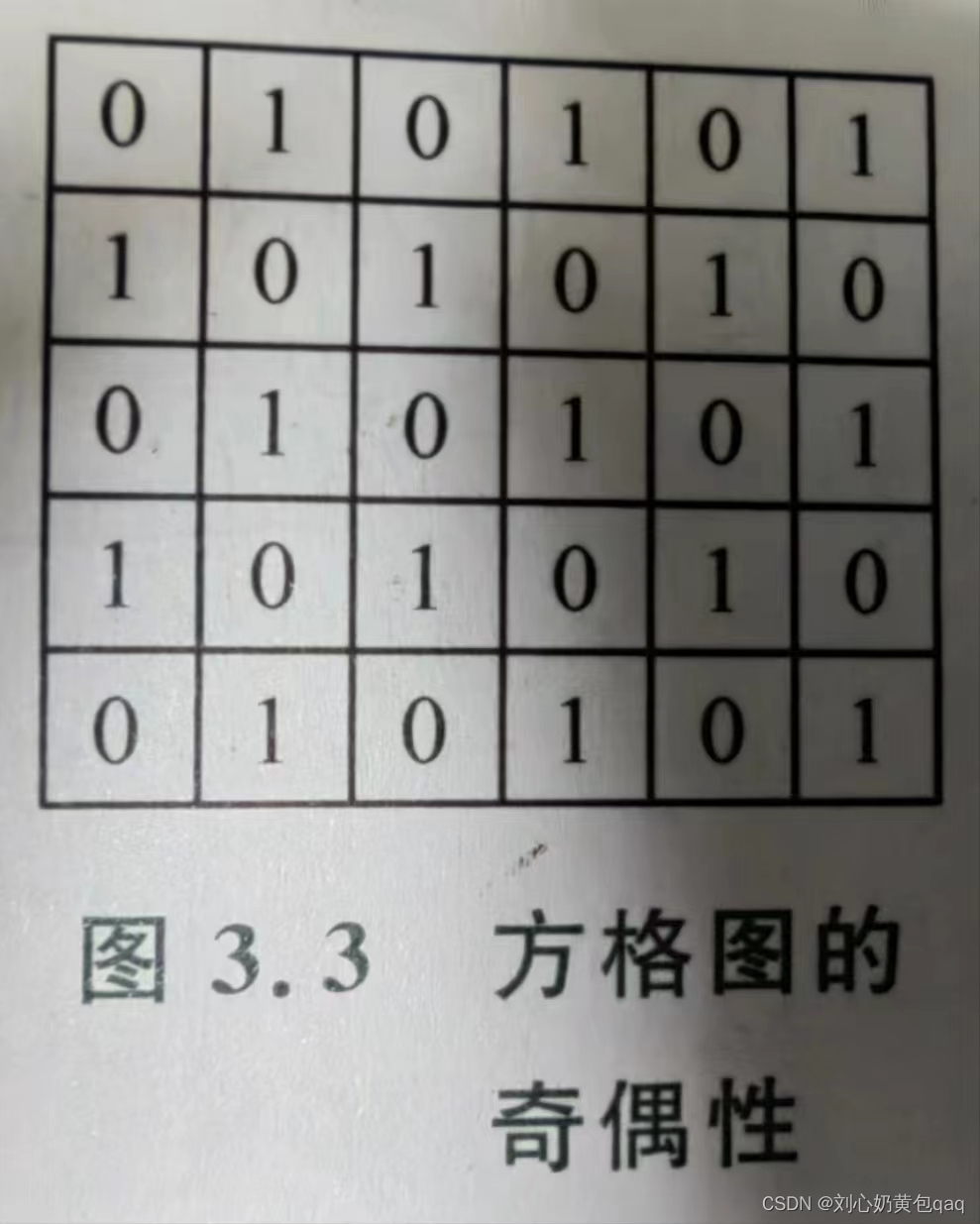
请添加图片描述

​ 起点和终点可以任意取，给定起点和终点以及T，可以立即判断是否有解：

​ （1）S、D同0或同1，当T为偶数时，可能有解，当T为奇数时，一定无解。

​ （2）S、D一个为1一个为0时，当T为奇数时，可能有解，当T为偶数时，一定无解。

​ 那么如何得知S、D的0，1情况呢，就看f（曼哈顿距离）的奇偶性，如果f为奇数，说明S、D一个为1，一个为0，如果f为偶数，说明S、D全为1或全为0。

​ 由上面知识可以知道，当T-f为奇数的时候，一定无解，就可以直接剪掉。

方格中允许有不可走的障碍，这些障碍不影响逻辑正确性

三、代码实现

#include<iostream>
using namespace std;
char biao[8][8];
int visit[8][8]={
   {
   0,0}};
int n,m,t;
int flag;				//标记是否找到答案
int a,b,c,d;
int dir[4][2]={
   {
   1,0},{
   -1,0},{
   0,1},{
   0,-1}};
#define CHECK(xx,yy) (xx>=0&&xx<n&&yy>=0&&yy<m)
void dfs(int x,int y,int step){
   
    if(flag)
        return;
    if(biao[x][y]=='D'){
   
        if(time==t)
            flag=1;
        return;
    }
    int temp=t-time-abs(c-x)-abs(d-y);
    if(temp<0)
        return ;//剪枝
    for(int i=0;i<4;i++){
   
        int xx=x+dir[i][0];
        int yy=y+dir[0][i];
        if(CHECK(xx,yy)&&biao[xx][yy]!='X'&&!visit[xx][yy]){
   
            visit[xx][yy]=1;
            bfs(xx,yy,step+1);
            visit[xx][yy]=0;
        }
    }
    return;
}
int main(){
   
    while(~scanf("%d%d%d",&n,&m,&t)){
   
        if(n==0&&m==0&&t==0)
            break;
        for(int i=0;i<n;i++){
   
            for(int j=0;j<m;j++){
   
                cin>>biao[i][j];
                if(biao[i][j]=='S'){
   
                    a=i;
                    b=j;
                }
                if(biao[i][j]=='D'){
   
                    c=i;
                    d=j;
                }
            }
        }
        memset(visit,0,sizeof(visit));
        int temp=t-abs(c-a)+abs(d-b);	//奇偶剪枝
        if(temp&1){
   
            cout<<"NO"<<endl;
            continue;
        }
        flag=0;
        visit[a][b]=1;
        dfs(a,b,0);
        if(flag)
            cout<<"YES"<<endl;
        else
            cout<<"NO"<<endl;
    }
    return 0;
}