0. 前置

1. 广义二项式定理（牛顿二项式定理）

我们重新定义组合数：

\[\dbinom rk=\dfrac{r^{\underline{k}}}{k!} \]

其中 $r^{\underline{k}}$ 是下降幂，$r\in\mathbb C,k\in\mathbb N$ .

注意 $r\in\mathbb C$ . 在这种情况下，对于任意 $\alpha\in\mathbb C$，有：

\[(1+x)^{\alpha}=\sum_{n\ge 0}\dbinom{\alpha}{n}x^n \]

2. 双阶乘

当 $n\in\mathbb N_+$ 时，$n$ 的双阶乘（$n!!$）表示不超过 $n$ 且与 $n$ 有相同奇偶性的所有正整数的乘积。

\[(2n)!!=2\times 4\times 6\times\cdots\times (2n) \]

\[(2n-1)!!=1\times 3\times 5\times\cdots\times (2n-1) \]

显然有递推式 $(n-2)!!n=n!!$，由此可以推导出：

\[(-2n-1)!!=\dfrac{(-1)^n}{|-1|\cdot|-3|\cdot|-5|\cdots\cdot|-2n+1|} \]

\[(-2n)\not\in \mathbb R \]

对于双阶乘有如下恒等式：

\[(2n)!!(2n-1)!!=(2n)! \]

\[(2n+1)!!(-2n-1)!!=(-1)^n(2n+1) \]

3. 一些展开式

\[(a+b)^n=\sum_{i=0}^n\dbinom{n}{i}a^ib^{n-i} \]

\[-\ln(-1-x)=x+\dfrac{x^2}{2}+\dfrac{x^3}{3}+\cdots \]

\[\exp(x)=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots \]

1. 形式幂级数的定义及基础运算（可略）

定义 形式幂级数（以下简称幂级数）为一个形如 $a_0+a_1x+a_2x^2+\cdots$ 形式的表达式。（注意：这里只是形式，不需要在意它表示什么），序列 $\{a_n\}$ 称之为它的 系数序列。称两个幂级数相等当且仅当它们的系数序列相同。

为简便，记 $[x^n]f(x)$ 表示幂级数 $f$ 的 $n$ 次项系数。另外，也用 $f(0)$ 表示 $f$ 的 $0$ 次项系数。

我们可以对其做一些运算，例如加法或减法。其定义是：

\[\sum_na_nx^n\pm\sum_nb_nx^n=\sum_n(a_n\pm b_n)x^n \]

幂级数的乘法由卷积来定义，即：

\[\left(\sum_na_nx^n\right)\cdot\left(\sum_nb_nx^n\right)=\sum_n c_nx^n \]

其中

\[c_n=\sum_k a_kb_{n-k} \]

现在你可以验证其满足各种我们所熟知的规律，比如加法交换律、加法结合律、乘法交换/结合律、乘法分配律等等（因此它们构成了一个环）。这些都很简单。

等下，说好的四则运算呢？还差一个除法 $\cdots$ 显然要定义除法，只需要定义逆元即 $f^{-1}$。但是有些幂级数是不可能有逆元的，比如首项系数为 $0$ 的幂级数。事实上这也是充要条件，即

幂级数 $f(x)=\sum_n a_nx^n$ 存在逆元当且仅当 $a_0\neq 0$

Proof：

必要性显然，因为若 $a_0=0$ 那么 $f$ 与任意幂级数的乘积的零次项系数都是 $0$ .

设 $f^{-1}=\sum_n b_nx^n$，那么 $f\cdot f^{-1}=1 \Longrightarrow \sum_k a_kb_{n-k}=[n=0]$，于是只需要令

\[b_n=\dfrac 1{a_0}\left([n=0]-\sum_{k>0}a_kb_{n-k}\right) \]

即可。
$\Huge \tag* □$

2. 生成函数

生成函数（Generating Function）又称母函数，是处理组合数学问题的一大利器。

它是一种形式幂级数，其每一项的系数可以提供关于这个序列的信息。

生成函数有许多不同的种类，但大多可以表示为单一的形式：

\[F(x)=\sum_{n}a_nk_n(x) \]

其中 $k_n(x)$ 被称为核函数。不同的核函数会导出不同的生成函数，拥有不同的性质。举个例子：

普通生成函数：$k_n(x)=x^n$；
指数生成函数：$k_n(x)=\dfrac{x^n}{n!}$；
狄利克雷生成函数：$k_n(x)=\dfrac{1}{n^x}$ .

同形式幂级数，我们常用 $[k_n(x)]F(x)$ 来表示它的第 $n$ 项的核函数对应的系数，也就是 $a_n$ .

1. 普通生成函数（OGF）

OGF 一般用来解决无标号有序的计数问题。

1. 定义

对于序列 $f=\langle f_0,f_1,f_2,\cdots\rangle$ 的普通生成函数（Ordinary Generating Function，OGF）为形式幂级数

\[F(x)=\sum_{i=0}^{\infty}f_ix^i \]

若已知序列 $\langle f_0,f_1,f_2,\cdots\rangle$，那么它的 OGF $F(x)$ 也随之确定；反之，如若以求得序列的 OGF $F(x)$，则该序列也随之确定。

常见 OGF：

OGF	序列
$1$	$\langle 1,0,0,0\cdots\rangle$
$\dfrac{1}{1-x}$	$\langle 1,1,1,1,\cdots\rangle$
$\dfrac{1}{(1-x)^2}$	$\langle 1,2,3,4,\cdots\rangle$
$\dfrac{1}{1+x}$	$\langle 1,-1,1,-1,\cdots\rangle$
$(1+x)^2$	$\langle 1,2,1,0,0,0,\cdots\rangle$
$(1+x)^4$	$\langle 1,4,6,4,1,0,0,0,\cdots\rangle$

对于 $\langle 1,1,1,1,,\cdots\rangle$ 的 OGF 是 $\dfrac{1}{1-x}$，是因为 $1+x+x^2+x^3+\cdots$ 在 $x\in(-1,1)$ 的时候，用等比数列求和公式：

\[\begin{aligned}1+x+x^2+\cdots &=\sum_{i=0}^n x^i\\&=\lim_{n\to \infty}\dfrac{1-x^n}{1-x}\\&=\dfrac{1}{1-x}\end{aligned} \]

这是因为 $\lim_{n\to \infty}x^n$ 在 $x\in(-1,1)$ 的时候收敛，值为 $0$ .

因为形式幂级数只是个形式，随便限制定义域没关系的。

由上式显然可以得到

\[\boxed{1+x^k+x^{2k}+\cdots = \dfrac{1}{1-x^k}} \]

只要罢 $X=x^k$ 代入即可。

把这个式子两端平方，得：

\[1+2x+3x^2+4x^3+\cdots=\dfrac{1}{(1-x)^2} \]

同理，把它两端 $k$ 次方，得到：

\[\boxed{\sum_{i}\dbinom{i+k-1}{k-1}x^i=\dfrac{1}{(1-x)^k}} \]

2. 性质

根据 OGF 的定义，容易发现 OGF 的运算和数列运算之间的关系：

\[\alpha F(x)+\beta G(x)=\sum_n(\alpha f_n+\beta g_n)x^n \]

\[x^mF(x)=\sum_n[n\ge m]f_{n-m}x^n \]

\[\dfrac{F(x)-\sum_{i=0}^{m-1}f_ix_i}{x^m}=\sum_n f_{n+m}x^n \]

\[F(cx)=\sum_n c^nf_nx^n \]

\[F'(x)=\sum_n(n+1)f_{n+1}x^n \]

\[\int_0^xF(t)\mathrm dt=\sum_{n}[n>0]\dfrac{f_{n-1}}{n}x^n \]

\[F(x)G(x)=\sum_n\left(\sum_{i=0}^nf_ig_{n-i}\right)x^n \]

注意最后一项是卷积的形式，这表明了 OGF 的乘积对应数列卷积。

通过上面的运算规则可以推出下面的式子：

OGF	序列
$\dfrac{1}{1-cx}$	$\langle 1,c,c^2,c^3\cdots\rangle$
$(1-x)^{-n}$	$\left\langle 1,n,\dbinom{n+1}{2},\dbinom{n+1}{3},\cdots\right\rangle$
$\ln \dfrac{1}{1-x}$	$\left\langle 0,1,\dfrac 12,\dfrac 13\cdots\right\rangle$
$\ln(1+x)$	$\left\langle 0,1,-\dfrac 12,\dfrac 13,-\dfrac 14\cdots\right\rangle$
$e^x$	$\left\langle 1,1,\dfrac 12,\dfrac 16,\dfrac{1}{24}\cdots\right\rangle$

你会发现以上都是一些看上去很简单的东西。那么生成函数到底哪里厉害了呢？

3. 示例

示例 1（Fibonacci 数列通项）

求 Fibonacci 数列通项，其中 Fibonacci 数列为 $f_n=\begin{cases}1 &n\le 1\\f_{n-1}+f_{n-2} &n>1\end{cases}$ .

设 $F(x)=f_0+f_1x+f_2x^2+f_3x^3+\cdots$，显然有：

\[\begin{aligned}F(x)&=&f_0+f_1x+f_2x^2+f_3x^3+\cdots\\xA&=&f_0x+f_1x^2+f_2x^3+\cdots\end{aligned} \]

前式减后式得 $x+x^2F(x)$，故 $F(x)=\dfrac{x}{1-x-x^2}$ .

注意到 $1-x-x^2=\left(1-\dfrac{1-\sqrt 5}{2}x\right)\left(1-\dfrac{1+\sqrt 5}{2}x\right)$，故：

\[\begin{aligned}\dfrac{x}{1-x-x^2}&=\dfrac{x}{\left(1-\dfrac{1-\sqrt 5}{2}x\right)\left(1-\dfrac{1+\sqrt 5}{2}x\right)}\\&=-\dfrac{1}{\sqrt 5}\dfrac{1}{1-\frac{1-\sqrt 5}{2}x}+\dfrac{1}{\sqrt 5}\dfrac{1}{1-\frac{1+\sqrt 5}{2}x}\end{aligned} \]

这就成了两个等比数列求和公式乘个常数再相加的形式了！把两个等比数列还原成数列，得到

\[f_n=-\dfrac{1}{\sqrt 5}\left(\dfrac{1-\sqrt 5}{2}\right)^n+\dfrac{1}{\sqrt 5}\left(\dfrac{1+\sqrt 5}{2}\right)^n \]

示例 2（Catalan 数列通项）

求 Catalan 数列通项，其中 Catalan 数列为 $H_n=\begin{cases}1&n=0\\\sum\limits_{i=0}^{n-1}H_iH_{n-i-1}&n>0\end{cases}$

当然也构造生成函数

\[\begin{aligned}H(x)&=\sum_n\left([n=0]+\sum_{i=0}^{n-1}f_if_{n-i-1}\right)x^n\\&=1+x\sum_n\left(\sum_{i=0}^{n-1}f_if_{n-i-1}\right)x^{n-1}\\&=1+xH^2(x)\end{aligned} \]

故 $xH^2(x)-H(x)+1=0$，解得 $H(x)=\dfrac{1\pm\sqrt{1-4x}}{2x}$

那么这就产生了一个问题：我们应该取哪一个根呢？我们将其分子有理化：

\[H(x)=\dfrac{2}{1\mp \sqrt{1-4x}} \]

代入 $x=0$ 得到的是 $H(x)$ 的常数项 $H_0$，当 $H(x)=\dfrac{2}{1+\sqrt{1-4x}}$ 时有 $H(0)=1$，满足要求，而另一个解会出现分母为 $0$ 的情况（不收敛），舍弃。

接下来我们要将其展开。但注意到它的分母不是斐波那契数列那样的多项式形式，因此不方便套用等比数列的展开形式。在这里我们需要使用牛顿二项式定理。我们来先展开 $\sqrt{1-4x}$：

\[\begin{aligned}(1-4x)^{\frac 12}&=\sum_{n\ge 0}\dbinom{\frac 12}{n}(-4x)^n\\&=1+\sum_{n\ge 1}\dfrac{\left(\frac 12\right)^n}{n!}(-4x)^n\end{aligned} \]

注意到

\[\begin{aligned}\left(\frac{1}{2}\right)^{\underline{n}}&=\frac{1}{2}\frac{-1}{2}\frac{-3}{2}\cdots\frac{-(2n-3)}{2}\\&=\frac{(-1)^{n-1}(2n-3)!!}{2^n}\\&=\frac{(-1)^{n-1}(2n-2)!}{2^n(2n-2)!!}\\&=\frac{(-1)^{n-1}(2n-2)!}{2^{2n-1}(n-1)!}\end{aligned} \]

这里使用了双阶乘的化简技巧。那么带回 $(1)$ 得到

\[\begin{aligned}(1-4x)^{\frac{1}{2}}&=1+\sum_{n\ge 1}\frac{(-1)^{n-1}(2n-2)!}{2^{2n-1}(n-1)!n!}(-4x)^n\\&=1-\sum_{n\ge 1}\frac{(2n-2)!}{(n-1)!n!}2x^n\\&=1-\sum_{n\ge 1}\binom{2n-1}{n}\frac{1}{(2n-1)}2x^n\end{aligned} \]

带回原式得到

\[\begin{aligned}H(x)&=\frac{1- \sqrt{1-4x}}{2x}\\&=\frac{1}{2x}\sum_{n\ge 1}\binom{2n-1}{n}\frac{1}{(2n-1)}2x^n\\&=\sum_{n\ge 1}\binom{2n-1}{n}\frac{1}{(2n-1)}x^{n-1}\\&=\sum_{n\ge 0}\binom{2n+1}{n+1}\frac{1}{(2n+1)}x^{n}\\&=\sum_{n\ge 0}\binom{2n}{n}\frac{1}{n+1}x^{n}\\\end{aligned} \]

这样我们就得到了卡特兰数的通项公式。

示例 3

在一个圆上的 $n$ 个点间，画出彼此不相交弦的全部方法的总数被称为默慈金数。它的前几项为 $M_0=1,M_1=1,M_2=2,M_3=4,M_4=9$ 其递推式为：

\[M_{n+2}=M_{n+1}+\sum_{i=0}^{n}M_iM_{n-i} \]

设生成函数为 $G(x)$，有：

\[\begin{aligned} G^2(x)&=M_0^2+(M_0M_1+M_1M_0)x+\cdots+\sum_{i=0}^nM_iM_{n-i}x^n+\cdots+\\&=M_0^2+(M_3-M_2)x+(M_4-M_3)x^2+...+(M_{n+2}-M_{n+1})x^n+...+\\&=1+\frac{1}{x^2}\left(M_0+M_1x+...+M_nx^n+...\right)-\frac{1}{x}\left(M_0+M_1x+...+M_nx^n+...\right)-\frac{1}{x^2}(M_0+M_1x+M_2x^2)+\frac{1}{x}(M_0+M_1x)\\&=\frac{1}{x^2}\left[G(x)-xG(x)-1\right]\\\end{aligned}\]

解得 $G(x)=\dfrac{1}{2x^2}\left[1-x-(1-2x-3x^2)^{\frac{1}{2}}\right]$，用牛顿二项式定理：

\[\begin{aligned}G(x)&=\frac{1}{2x^2}\left[1-x-\left(1+{\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n\cdot2^{2n-1}}\cdot+C_{2n-2}^{n-1}(-2x-3x^2)^n}\right)\right]\\&=\frac{1}{2x^2}\left[-x+\sum_{n=1}^{\infty}\frac{1}{n\cdot2^{2n-1}}\cdot+C_{2n-2}^{n-1}(2x+3x^2)^n\right]\\&=\frac{1}{2x^2}\left[-x+\sum_{n=1}^{\infty}\frac{1}{n\cdot2^{2n-1}}\cdot+C_{2n-2}^{n-1}\sum_{k=0}^nC_n^k(2x)^{n-k}(3x^2)^{k}\right]\\\end{aligned} \]

示例 4

有三种物品，分别有 $3,2,3$ 个，问拿出 $4$ 个进行组合（无序）的方案数是多少。

对每个物品构造一个序列 $\{a_n\}$，$a_i$ 表示取了 $i$ 个的方案数。

容易发现，这三个序列的 OGF 分别是：

$F_1(x)=1+x+x^2+x^3$；
$F_2(x)=1+x+x^2$；
$F_3(x)=1+x+x^2+x^3$；

把它们乘起来然后取第 $4$ 项系数即可。

示例 5（经典题）

食物

在许多不同种类的食物中选出 $n$ 个，每种食物的限制如下：

承德汉堡：偶数个
可乐：$0$ 个或 $1$ 个
鸡腿：$0$ 个，$1$ 个或 $2$ 个
蜜桃多：奇数个
鸡块：$4$ 的倍数个
包子：$0$ 个，$1$ 个，$2$ 个或 $3$ 个
土豆片炒肉：不超过一个
面包：$3$ 的倍数个

每种食物都是以「个」为单位，只要总数加起来是 $n$ 就算一种方案。对于给出的 $n$ 你需要计算出方案数，对 $10007$ 取模。

把每种食物的 OGF 写出来：

承德汉堡：$1+x^2+x^4+\cdots=\dfrac{1}{1-x^2}$
可乐：$1+x$
鸡腿：$1+x+x^2=\dfrac{1-x^3}{1-x}$
蜜桃多：$x+x^3+x^5+\cdots=x(1+x^2+x^4+\cdots)=\dfrac{x}{1-x^2}$
鸡块：$1+x^4+x^8+\cdots=\dfrac{1}{1-x^4}$
包子：$1+x+x^2+x^3=\dfrac{1-x^4}{1-x}$
土豆片炒肉：$1+x$
mian 包：$1+x^3+x^6+\cdots=\dfrac{1}{1-x^3}$

全乘起来，很多都约掉了，得到 $\dfrac{x}{1-x^4}$，即

\[\sum_{n\ge 1} \dbinom{n+2}{n-1}x^n \]

因此答案就是 $\dbinom{n+2}{n-1}=\dbinom{n+2}{3}$ .

示例 6（背包）

Euler 无标号计数：

你有很多物品，体积为 $i$ 的有 $a_i$ 种，每种物品数量无限。求选取物品使得它们大小之和恰好为为 $n$ 的方案数，元素无序。

这不就是背包问题吗？所以背包问题是最经典的无标号计数。

~~其实这题和 OGF 根本没有关系，背包裸题，写个 dp 即可。~~

如果按照原来的思路直接上 OGF 显然会暴毙。因为这道题装物品这个动作已经变成无序的了。

于是我们考虑拿了体积为 $i$ 的物品多少个这个问题，惊奇的发现这个问题就是可以强行钦定顺序的了！我们可以先尝试拿了多少个体积为 $1$ 的，再尝试拿了多少个体积为 $2$ 的 $\cdots$

由于体积为 $i$ 的有 $a_i$ 种，于是如果我们只拿体积为 $i$ 的能组成每个体积的方案数量为

\[(x^0+x^i+x^{2i}+\cdots)^{a_i} \]

我们就得到了 Euler 变换：

\[\operatorname{Euler}(F(x))=\prod_{i=0}^n\left(\dfrac{1}{1-x^i}\right)^{a_i} \]

往往这种不太好处理的求积可以先 $⁡\ln$ 再 $⁡\exp$：

\[\begin{aligned}\operatorname{Euler}(F(x))&=\prod_{i=0}\left(\dfrac{1}{1-x^i}\right)^{a_i}\\&=\exp\left(\sum_{i=1}^n\ln((1-x^i)^-1\right)\\&=\exp\left(\sum_{i=1}^n-\ln(1-x^i)\right)\\&=\exp\left(\sum_{i=1}^n\sum_{j\ge 1}\dfrac{x^{ij}}{j}\right)\\&=\exp\left(\sum_{j\ge 1}\dfrac{\sum_{i=1}^na_ix^{ij}}{j}\right)\end{aligned} \]

设 $\{a_ix^i\}$ 的生成函数是 $G(x)$，那么

\[=\exp\left(\sum_{j\ge 1}\dfrac{G(x_j)}{j}\right) \]

这样我们就知道了

\[\boxed{\operatorname{Euler}(F(x))=\exp\left(\sum_{j\ge 1}\dfrac{G(x_j)}{j}\right)} \]

这个枚举 $j$ 算出 $\dfrac{G(x_j)}{j}$ 算出来求和再 $\exp$ 就完了，复杂度 $O(n\log n)$ .

例题：

示例 6（推恒等式）

显然：

\[(1+x)^r=\sum_{k\ge 0}\dbinom{r}{k}x^k \]

\[(1+x)^s=\sum_{k\ge 0}\dbinom{s}{k}x^k \]

把这两个相乘得到：

\[(1+x)^r(1+x)^s=(1+x)^{r+s} \]

令这个等式两端 $x^n$ 的系数相等，得：

\[\sum_{k=0}^n\dbinom{r}{k}\dbinom{s}{n-k}=\dbinom{r+s}{n} \]

我们就发现了范德蒙德卷积！

示例 7

休闲娱乐一下：

拯救世界：

我们要召唤 kkksc03 和 lzn 两位大神，召唤他们需要五行神石。

kkksc03 大神召唤方法：

金神石的块数必须是 $6$ 的倍数。
木神石最多用 $9$ 块。
水神石最多用 $5$ 块。
火神石的块数必须是 $4$ 的倍数。
土神石最多用 $7$ 块。

lzn 大神召唤方法:

金神石的块数必须是 $2$ 的倍数。
木神石最多用 $1$ 块。
水神石的块数必须是 $8$ 的倍数。
火神石的块数必须是 $10$ 的倍数。
土神石最多用 $3$ 块。

有 $n$ 块混沌之石，这 $n$ 块混沌之石可以被认为是任意一种五行神石，求召唤这两位大神的方案数。

kkksc03：

金神石：$1+x^6+x^{12}+\cdots=\dfrac{1}{1-x^6}$
木神石：$1+x+x^2+\cdots+x^9=\dfrac{1-x^{10}}{1-x}$
水神石：$1+x+x^2+\cdots+x^5=\dfrac{1-x^6}{1-x}$
火神石：$1+x^4+x^8+\cdots=\dfrac{1}{1-x^4}$
土神石：$1+x+x^2+\cdots+x^7=\dfrac{1-x^8}{1-x}$

lzn：

金神石：$1+x^2+x^4+\cdots=\dfrac{1}{1-x^2}$
木神石：$1+x=\dfrac{1-x^2}{1-x}$
水神石：$1+x^8+x^{16}+\cdots=\dfrac{1-x^8}{1-x}$
火神石：$1+x^{10}+x^{20}+\cdots=\dfrac{1}{1-x^{10}}$
土神石：$1+x+x^2+x^3=\dfrac{1-x^4}{1-x}$

乘起来就是

\[\dfrac{1}{1-x^5}=\sum_k\dbinom{k+4}{k}x^i \]

所以答案就是 $\dbinom{k+4}{k}=\dfrac{(k+1)(k+2)(k+3)(k+4)}{24}$ .

注意高精要写 NTT .

Tips

有些题不用对 OGF 进行推导，直接暴力乘开（或者 NTT？）即可。

2. 指数生成函数（EGF）

EGF 一般用来解决有标号有序的计数问题。

1. 定义

对于序列 $f=\langle f_0,f_1,f_2,\cdots\rangle$ 的普通生成函数（Exponential Generating Function，EGF）为形式幂级数

\[\hat F(x)=\sum_{i=0}^{\infty}f_i\dfrac{x^i}{i!} \]

同样的，若已知序列 $\langle f_0,f_1,f_2,\cdots\rangle$，那么它的 EGF $\hat F(x)$ 也随之确定；反之，如若以求得序列的 EGF $\hat F(x)$，则该序列也随之确定。

注意指数生成函数的乘法运算：对于两个序列 $a,b$ ，设它们的指数生成函数分别为 $\hat{F}(x),\hat{G}(x)$ ，那么

\[\begin{aligned}\hat{F}(x)\hat{G}(x)&=\sum_{i\ge 0}a_i\frac{x^i}{i!}\sum_{j\ge 0}b_j\frac{x^j}{j!}\\&=\sum_{n\ge 0}x^{n}\sum_{i=0}^na_ib_{n-i}\frac{1}{i!(n-i)!}\\&=\sum_{n\ge 0}\frac{x^{n} }{n!}\sum_{i=0}^n\binom{n}{i}a_ib_{n-i}\end{aligned} \]

因此 $\hat{F}(x)\hat{G}(x)$ 是序列 $\left\langle \sum\limits_{i=0}^n \dbinom{n}{i}a_ib_{n-i} \right\rangle$ 的指数生成函数。

多出来的 $\dbinom ni$ 告诉我们它适用于排列的计算（相对于 OGF 的普通卷积对应组合）

2. 性质

EGF 运算法则：

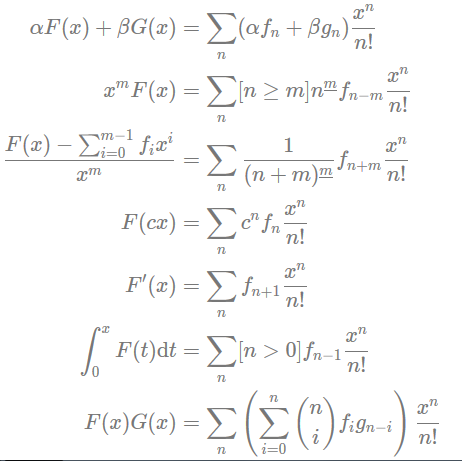
同样有一些基本的 EGF：

EGF	数列
$e^x$	$\langle1,1,1,\cdots\rangle$
$xe^x$	$\langle0,1,2,\cdots\rangle$
$e^{cx}$	$\langle 1,c,c^2,\cdot\rangle$
$\cdots$	$\cdots$

其实你只需要注意到 $\langle f_n\rangle$ 的 EGF 实际上就是 $\langle \dfrac{f_n}{x!}\rangle$ 的 OGF，就能找到不少例子。

$\begin{aligned} \hat { G } ( x ) &= 1 + x + \frac { x ^ { 2 } } { 2 ! } + \frac { x ^ { 3 } } { 3 ! } + \ldots = e ^ { x }\\ \hat { G } ( x ) &= 1 - x + \frac { x ^ { 2 } } { 2 ! } - \frac { x ^ { 3 } } { 3 ! } + \ldots = e ^ { - x }\\ \hat { G } ( x ) &= 1 + \frac { x ^ { 2 } } { 2 ! } + \frac { x ^ { 4 } } { 4 ! } + \frac { x ^ { 6 } } { 6 ! } + \ldots = \frac { e ^ { x } + e ^ { - x } } { 2 }\\ \hat { G } ( x ) &= x + \frac { x ^ { 3 } } { 3 ! } + \frac { x ^ { 5 } } { 5 ! } + \frac { x ^ { 7 } } { 7 ! } + \ldots = \frac { e ^ { x } - e ^ { - x } } { 2 }\\ \hat { G } ( x ) &= x - \frac { 1 } { 2 } x ^ { 2 } + \frac { 1 } { 3 } x ^ { 3 } +\cdots=\ln ( 1 + x )\\ \hat { G } ( x ) &=x - \frac { 1 } { 3 ! } x ^ { 3 } + \frac { 1 } { 5 ! } x ^ { 5 }+\cdots=\sin x\\ \hat { G } ( x ) &=x + \frac { 1 } { 2 } \times \frac { x ^ { 3 } } { 3 } + \frac { 1 \times 3 } { 2 \times 4 } \times \frac { x ^ { 5 } } { 5 } + \frac { 1 \times 3 \times 5 } { 2 \times 4 \times 6 } \times \frac { x ^ { 7 } } { 7 }=\arcsin x\\ \hat { G } ( x ) &=1 - \frac { 1 } { 2 ! } x ^ { 2 } + \frac { 1 } { 4 ! } x ^ { 4 } +\cdots=\cos x\\ \hat { G } ( x ) &=1 + \frac { a } { 1 ! } x + \frac { a ( a - 1 ) } { 2 ! } x ^ { 2 } + \frac { a ( a - 1 ) ( a - 2 ) } { 3 ! } x ^ { 3 }+\cdots=(1+x)^a \end{aligned}$

那么 EGF 哪里又厉害了呢？

3. 示例

示例 1（圆排列多项式 exp）

长度为 $n$ 的排列数的指数生成函数是

\[\hat{P}(x)=\sum_{n\ge 0}\frac{n!x^n}{n!}=\sum_{n\ge 0}x^n=\frac{1}{1-x} \]

圆排列的定义是把 $1,2,\cdots,n$ 排成一个环的方案数。也就是说旋转后的方案的等价的（但翻转是不等价的）。

$n$ 个数的圆排列数显然是 $(n-1)!$ 。因此 $n$ 个数的圆排列数的指数生成函数是

\[\hat{Q}(x)=\sum_{n\ge 1}\frac{(n-1)!x^n}{n!}=\sum_{n\ge 1}\frac{x^n}{n}=-\ln(1-x)=\ln\left( \frac{1}{1-x} \right) \]

也就是说 $\exp \hat{Q}(x)=\hat{P}(x)$ 。但这只是数学层面的推导。我们该怎样直观理解：圆排列数的 EGF 的 $\exp$ 是排列数的 EGF？

一个排列，是由若干个置换环构成的。例如 $p=[4,3,2,5,1]$ 有两个置换环：

（也就是说我们从 $p_i$ 向 $i$ 连有向边）

而不同的置换环，会导出不同的排列。例如我将第二个置换环改成

那么它对应的排列就是 $[5,3,2,1,4]$ 。

也就是说，长度为 $n$ 的排列的方案数是

把 $1,2,\cdots,n$ 分成若干个集合
每个集合形成一个置换环

的方案数。而一个集合的数形成置换环的方案数显然就是这个集合大小的圆排列方案数。因此长度为 $n$ 的排列的方案数就是：把 $1,2\cdots,n$ 分成若干个集合，每个集合的圆排列方案数之积。

这就是多项式 $\exp$ 的直观理解。

推广之

如果 $n$ 个点 带标号 生成树的 EGF 是 $\hat{F}(x)$ ，那么 $n$ 个点 带标号 生成森林的 EGF 就是 $\exp \hat{F}(x)$ ——直观理解为，将 $n$ 个点分成若干个集合，每个集合构成一个生成树的方案数之积。
如果 $n$ 个点带标号无向连通图的 EGF 是 $\hat{F}(x)$ ，那么 $n$ 个点带标号无向图的 EGF 就是 $\exp \hat{F}(x)$ ，后者可以很容易计算得到 $\exp \hat{F}(x)=\sum\limits_{n\ge 0}2^{\binom{n}{2}}\dfrac{x^n}{n!}$ 。因此要计算前者，只需要一次多项式 $\ln$ 即可。

Text^[1]

Refence

浅谈 OI 中常用的一些生成函数运算的合法与正确性 - _rqy
生成函数简介 - _rqy
生成函数简介 - OI Wiki
普通生成函数 - OI Wiki
组合数学——母函数与递推 - 朱全民
趣谈生成函数 =v= - 胡小兔
小学生都能看懂的生成函数入门教程 - 自为风月马前卒；牛客版；知乎版
利用生成函数求斐波那契数列通项公式 - 自为风月马前卒
双阶乘 - 百度百科
生成函数及应用 - ACdreamer
生成函数与组合计数初探 - yijan
题解 P4389 【付公主的背包】 - command_block
[数学记录]P5900 无标号无根树计数 - command_block
多项式计数杂谈 - command_block
Concrete Mathematic $\;$ A Foundation for Computer Scinece, Second Edition - Ronale L. Graham ; Donale E. Knuth ; Oren Patashink
指数生成函数 - OI Wiki

Desc ↩︎

</section>

OGF	序列
\(1\)	\(\langle 1,0,0,0\cdots\rangle\)
\(\dfrac{1}{1-x}\)	\(\langle 1,1,1,1,\cdots\rangle\)
\(\dfrac{1}{(1-x)^2}\)	\(\langle 1,2,3,4,\cdots\rangle\)
\(\dfrac{1}{1+x}\)	\(\langle 1,-1,1,-1,\cdots\rangle\)
\((1+x)^2\)	\(\langle 1,2,1,0,0,0,\cdots\rangle\)
\((1+x)^4\)	\(\langle 1,4,6,4,1,0,0,0,\cdots\rangle\)

OGF	序列
\(\dfrac{1}{1-cx}\)	\(\langle 1,c,c^2,c^3\cdots\rangle\)
\((1-x)^{-n}\)	\(\left\langle 1,n,\dbinom{n+1}{2},\dbinom{n+1}{3},\cdots\right\rangle\)
\(\ln \dfrac{1}{1-x}\)	\(\left\langle 0,1,\dfrac 12,\dfrac 13\cdots\right\rangle\)
\(\ln(1+x)\)	\(\left\langle 0,1,-\dfrac 12,\dfrac 13,-\dfrac 14\cdots\right\rangle\)
\(e^x\)	\(\left\langle 1,1,\dfrac 12,\dfrac 16,\dfrac{1}{24}\cdots\right\rangle\)

EGF	数列
\(e^x\)	\(\langle1,1,1,\cdots\rangle\)
\(xe^x\)	\(\langle0,1,2,\cdots\rangle\)
\(e^{cx}\)	\(\langle 1,c,c^2,\cdot\rangle\)
\(\cdots\)	\(\cdots\)

生成函数（母函数）详解

0. 前置

1. 广义二项式定理（牛顿二项式定理）

2. 双阶乘

3. 一些展开式

1. 形式幂级数的定义及基础运算（可略）

2. 生成函数

1. 普通生成函数（OGF）

1. 定义

2. 性质

3. 示例

示例 1（Fibonacci 数列通项）

示例 2（Catalan 数列通项）

示例 3

示例 4

示例 5（经典题）

示例 6（背包）

Tips

2. 指数生成函数（EGF）

1. 定义

2. 性质

3. 示例

示例 1（圆排列 多项式 exp）

Refence

示例 1（圆排列多项式 exp）