基础数据结构——1.1链表

洛谷 P1996 约瑟夫问题

时间限制：1.00s　　内存限制：125.00MB

题目描述

有 $n$ 个人，编号为 $1\sim n$ ，按顺序围成一圈，从第 1 个人开始报数，数到 $m$ 的人出列，再由下一个人重新从 $1$ 开始报数，数到 $m$ 的人再出圈，依次类推，直到所有的人都出圈，请输出依次出圈人的编号。

输入格式

输入两个整数 $n, m$ 。

输出格式

输出一行 $n$ 个整数，按顺序输出每个出圈人的编号。

样例输入
10 3
样例输出
3 6 9 2 7 1 8 5 10 4
提示

$1 \le m, n \le 100$

1.1.2 静态链表¹

双向链表

构建双向链表

将每个人都视为一个元素，每个元素都有以下 3 种信息：

本人的编号 $n u m$ .
本人相邻的下一个人的编号 $n x t$ .
本人相邻的上一个人的编号 $p r e$ .

在一开始，所有人围成一圈，对于编号为 $i$ 的人，有：

$n u m [i] = i$ .
$n x t [i] = i + 1$ .
$p r e [i] = i - 1$ .

特别地，对于本题，由于人是围成一圈的，所以编号为 $1$ 的人的 $p r e [1] = n$ ，编号为 $n$ 的人的 $n x t [n] = 1$ .

双向链表如图1.1.1所示.

图1.1.1 双向链表

对于链表中的元素，用结构体（struct）数组或多个数组实现均可.

删除双向链表中的元素

从编号为 1 的人开始报数，数到 $m$ 的人需要出列，设出列的人编号为 $x$ ，则：

$n x t [p r e [x]] = n x t [x]$ ，即与编号为 $x$ 的人相邻的上一个人编号为 $p r e [x]$ ，现在他相邻的下一个人的编号为 $n x t [x]$ .
$p r e [n x t [x]] = p r e [x]$ ，即与编号为 $x$ 的人相邻的下一个人编号为 $n x t [x]$ ，现在他相邻的上一个人的编号为 $p r e [x]$ .

如图1.1.2所示，虽然编号为 $x$ 的人元素没有被真正删除，但编号为 $x$ 的人已经不会再参与报数了.

图1.1.2 删除双向链表中的元素

有如下代码片段：

//代码片段-双向链表删除编号为 x 的元素
void del(int x) {
	nxt[pre[x]] = nxt[x];
	pre[nxt[x]] = pre[x];
}

代码实现

设编号为 $x$ 的人的报数为 $c n t$ ，则在一开始有 $x=1,\;cnt=1$ ，则：

若所有人都已出列，则结束算法，否则跳转到 2.
若当前的编号为 $x$ 的人的报数 $c n t = m$ ，则此人出列且 $c n t = 0$ （方便下一个人报数为 1），不论此人是否出列都跳转到 3.
让 $x=nxt[x],\; cnt=cnt+1$ ，即让与编号为 $x$ 的人相邻的下一个进行报数，随后跳转到 1.

Q：这里会发现，当最后一个人出列后，仍让最后一个人的下一个人报数，这看起来很荒谬，但为什么算法执行结果却没有问题？

A：因为与最后一个人相邻的上一个人和下一个人都是他自己，所以算法执行的结果是没有问题的；并且这不是本题唯一的算法，本算法是先判断是否出列再让下一个人报数的算法，也可以设计出一种先让人报数再判断是否出列的算法，从而规避掉这种现象.

如下为使用数组模拟双向链表的参考代码.

//洛谷P1996约瑟夫问题-静态链表-双向链表写法
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
int num[N], nxt[N], pre[N];
int main() {
	int n, m; 
    scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; ++i) {
		num[i] = i;
		nxt[i] = i + 1;
		pre[i] = i - 1;
	}
	pre[1] = n; nxt[n] = 1;
	int x = 1, cnt = 1; // cnt 为编号为 x 的人的报数
	while (n) {
		if (cnt == m) { // 若编号为 x 的人报数为 m
			--n; // 此人出列
			printf("%d ", num[x]);
			nxt[pre[x]] = nxt[x];
			pre[nxt[x]] = pre[x];
			cnt = 0; // cnt 此处清零，则下一个人的报数即为 1
		}
		x = nxt[x]; // 让编号为 x 的人原本相邻的下一个人进行报数
		++cnt;
		/*
			注意这里先判断编号为 x 的人报数是否为 m，再让下一个人进行报数
			因为 m 可能等于 1，所以一开始报数的人就有可能出列
		*/
	}
	return 0;
}

在 bits/stdc++.h 头文件中引用了绝大部分 C++ STL 的其他头文件，故其也被称为“万能头文件”，引用了该头文件后，一般不需要再引用其他头文件.

在算法竞赛中一般是可以使用的.

时间复杂度分析

由于每次报数为 $m$ 的人才会出列，总共有 $n$ 个人，所以总共需要报数 $m\times n$ 次才能让所有人都出列.

本代码就是模拟的一个报数的过程，故时间复杂度为 $O(m\times n)$ .

向双向链表中插入元素*²

若想要在编号为 $x$ 的人之后插入一个编号为 $y$ 的人，则：

$n x t [y] = n x t [x]$ ， $p r e [y] = x$ ，即原本与编号为 $x$ 的人相邻的下一个人，现在变成与编号为 $y$ 的人相邻的下一个人了.
$p r e [n x t [x]] = y$ ， $n x t [x] = y$ ，即现在与编号为 $x$ 的人相邻的下一个人，变成了编号为 $y$ 的人.

在放入编号为 $y$ 的人之前，编号为 $x$ 的人相邻的下一个人的编号只能用 $n x t [x]$ 表示.

为了避免因为 $n x t [x] = y$ 这一赋值操作而丢失编号丢失， $p r e [n x t [x]] = y$ 必须在 $n x t [x] = y$ 之前执行.

插入操作如图1.1.3所示.

图1.1.3 向双向链表中插入元素

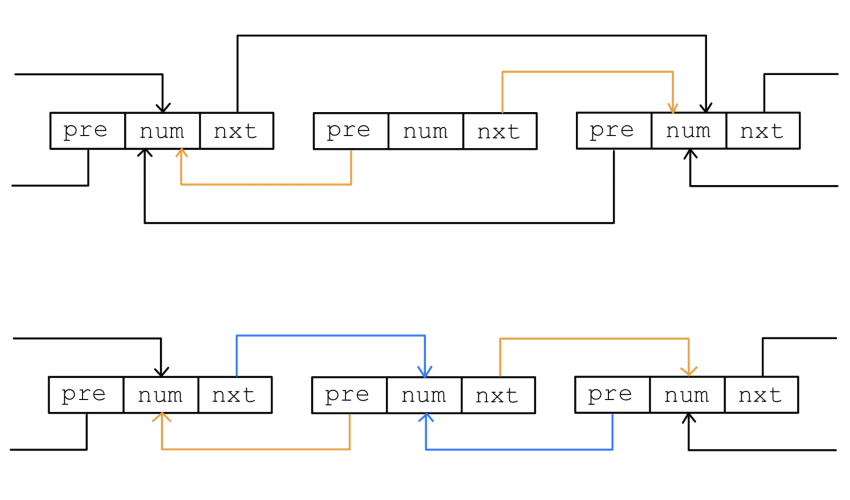
有如下代码片段：

//代码片段-双向链表在编号为 x 的元素之后插入编号为 y 的元素
void add(int x, int y) {
	nxt[y] = nxt[x];
	pre[y] = x;
	pre[nxt[x]] = y;
	nxt[x] = y;
}

关于本代码片段

链表中的元素所记录的信息不一定只有 $n u m$ 一种，存在多种信息时可以用多个数组或结构体来实现.

类似的，可以推导出，若想要在编号为 $x$ 的人之前插入一个编号为 $y$ 的人，有如下代码片段：

//代码片段-双向链表在编号为 x 的元素之前插入编号为 y 的元素
void add(int x, int y) {
	nxt[y] = x;
	pre[y] = pre[x];
	nxt[pre[x]] = y;
	pre[x] = y;
}

类似的， $n x t [p r e [x]] = y$ 必须在 $p r e [x] = y$ 之前执行，理由与上面的描述相同.

表头和`NULL`*

本题的链表比较特殊，由于人是围成一圈的，所以本题的链表没有一般意义上的开头和结尾，但一般的链表是有开头和结尾的.

表头 $h e a d$ ：链表的开头，一般来说表头只是存储链表开头的元素的位置（数组下标）.
一般的链表会有最后一个元素，而最后一个元素的 $n x t$ 一般会存储一个 -1（ $n x t$ 存储数组下标时）或者 NULL（ $n x t$ 存储元素地址时），来表示当前链表的最后一个元素后面已经没有元素了.

特别地，对于空的链表一般有 $h e a d = - 1$ ，对于链表内的第一个元素其 $p r e = - 1$ .

带表头的双向链表如图1.1.4所示.

图1.1.4 带表头的双向链表

还有一种表头的定义即 $h e a d$ 为链表中的第一个元素，其也会有保存的信息和 $nxt,\,pre$ .

将元素插入在双向链表的开头*

由于在链表中某个位置之后/之前插入一个元素时，需要先找到对应的位置才能进行插入，所以一般较为常用的是将元素直接插入在链表的开头：

将编号为 $x$ 的元素插入到双向链表的开头，有：

$n x t [x] = h e a d$ ， $p r e [x] = - 1$ ，注意 $h e a d$ 存储的是链表开头的元素（数组下标）.
$p r e [h e a d] = x$ ， $h e a d = x$ ，注意若链表为空则不需要 $p r e [h e a d] = x$ 这一语句.

将元素插入在双向链表的开头如图1.1.5所示.

图1.1.5 将元素插入在双向链表的开头

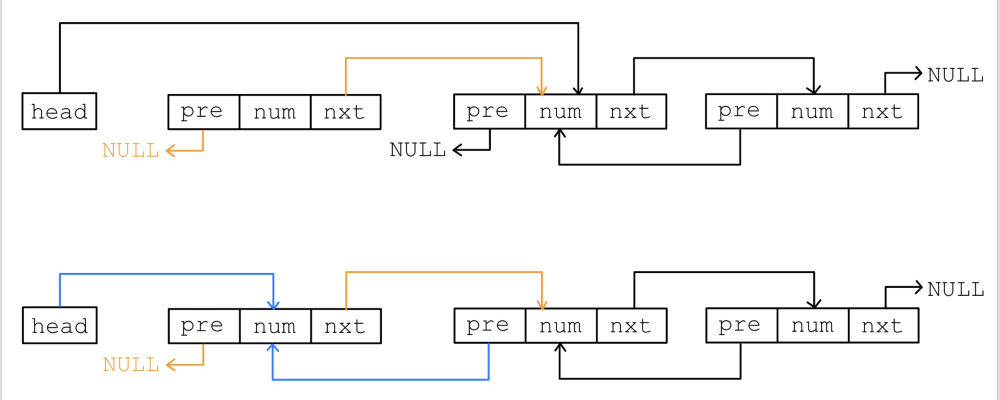
有如下代码片段：

//代码片段-将元素插入在双向链表的开头
void add_head(int x) {
	nxt[x] = head;
	pre[x] = -1;
	if (head != -1) pre[head] = x; // 默认链表为空时有 head=-1，为防止数组下标越界需要判断
	head = x;
}

类似的，这里直接给出删除双向链表开头元素的代码片段：

//代码片段-删除双向链表开头元素
void del_head(int x) {
	if (nxt[head] != -1) pre[nxt[head]] = -1; // 由于链表可能只有这一个元素，为防止数组下标越界需要判断
	head = nxt[head];
}

由于有了表头和 NULL 的概念，在插入和删除链表元素时，需要时刻注意：

需要插入的元素是否在开头、结尾，若在开头则其 $p r e = - 1$ ，若在结尾则其 $n x t = - 1$ .
需要删除的元素是否在开头、结尾，若在开头则其后一个元素（如果有的话）的 $p r e = - 1$ ，若在结尾则其前一个元素的 $n x t = - 1$ .

对于双向链表，其基本功能有如下代码片段：

//将元素插入在双向链表的开头
void add_head(int x) {
	nxt[x] = head;
	pre[x] = -1; // 在链表开头的元素的 pre = -1
	if (head != -1) pre[head] = x; 
    /*
    	如果 head != -1，说明链表中有元素
    	应有该元素的 pre = x
    */
	head = x;
}
//删除双向链表开头元素
void del_head() {
	if (nxt[head] != -1) pre[nxt[head]] = -1;
    /*
    	如果链表开头的元素的 nxt != -1，说明它后面还有元素
    	则它后面的元素在删除链表开头的元素后，变成了新的链表开头的元素，其 pre = -1
    */
	head = nxt[head];
}
//双向链表在编号为 x 的元素之前插入编号为 y 的元素
void add_L(int x, int y) {
	nxt[y] = x;
	pre[y] = pre[x];
	if (pre[x] == -1) head = y;
	else nxt[pre[x]] = y;
    /*
    	如果 x 是链表开头的元素（即其 pre = -1）
    	那么在 x 之前插入的 y 就会变成链表开头的元素，即 head = y
    	否则 x 之前也有元素，此元素的 nxt = y
    */
	pre[x] = y;
}
//双向链表在编号为 x 的元素之后插入编号为 y 的元素
void add_R(int x, int y) {
	nxt[y] = nxt[x];
	pre[y] = x;
	if (nxt[x] != -1) pre[nxt[x]] = y;
    /*
    	如果 x 不是链表最后一个元素（即其 nxt != -1）
    	则存在 x 后面的元素的 pre = y
    */
	nxt[x] = y;
}
//双向链表删除编号为 x 的元素
void del(int x) {
	if (pre[x] == -1)  head = nxt[x];
	else nxt[pre[x]] = nxt[x];
    /*
    	如果 x 是链表开头的元素（即其 pre = -1）删除它后有 head = nxt[x]
    	否则存在 x 前面的元素，其 nxt = nxt[x]
    */
	if (nxt[x] != -1) pre[nxt[x]] = pre[x];
    /*
    	如果 x 不是链表最后一个元素（即其 nxt != -1）
    	则存在 x 后面的元素的 pre = pre[x]
    */
}

单向链表

构建单向链表

可以发现，在本题中，记录相邻的上一个人的编号并不重要，因为总是让相邻的下一个人进行报数，所以所有元素中 $p r e$ 信息都不需要记录.

单向链表如图1.1.6所示.

图1.1.6 单向链表

### 删除单向链表中的元素

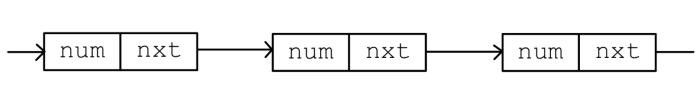
对于单向链表来说，设需要删除的元素为 $x$ ，则需要知道其前一个元素 $y$ ，有：

$n x t [y] = n x t [x]$ ，即其前一个元素 $y$ 直接指向其后一个元素，即可完成删除.
由于 $n x t [y] = x$ ，故如上语句也可以直接写成 $n x t [y] = n x t [n x t [y]]$ .

有如下代码片段：

//代码片段-删除单向链表中的元素
void del(int y) {
	nxt[y] = nxt[nxt[y]];
}

代码实现

设编号为 $x$ 的人的报数为 $c n t$ ，为了方便删除元素，所以在一开始有 $x=0,\;cnt=n$ ，则：

若所有人都已出列，则结束算法，否则跳转到 2.
若当前的编号为 $x$ 的人的报数 $c n t = m - 1$ ，则其相邻的下一个人出列且 $c n t = 0$ （方便下一个人报数为 1），不论是否有人出列都跳转到 3.
让 $x=nxt[x],\; cnt=cnt+1$ ，即让与编号为 $x$ 的人相邻的下一个进行报数，随后跳转到 1.

如下为使用数组模拟单向链表的参考代码.

//洛谷P1996约瑟夫问题-静态链表-单向链表写法
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
int nxt[N]; // 因为第 i 个人的编号就是 i，所以可以省略 num
int main() {
	int n, m; 
    scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; ++i) 
		nxt[i] = i + 1;
	nxt[n] = 1;
	int x = n, cnt = 0;
	/*
		第 1 个报数的人编号为 1，则在报数开始之前
		可以认为第 0 个报数的人编号为 n，报数为 0
	*/
	while (n) {
		if (cnt == m - 1) {
			/*
				对于当前编号为 x 的人来说，若他的报数为 m-1
				则他相邻的下一个人的编号为 nxt[x]、报数为 m
			*/
			--n;
			printf("%d ", nxt[x]);
			nxt[x] = nxt[nxt[x]];
			cnt = 0;
		}
		x = nxt[x];
		++cnt;
	}
	return 0;
}

时间复杂度分析

本代码时间复杂度为 $O(m\times n)$ .

向单向链表中插入元素*

若想要在编号为 $x$ 的元素之后插入一个编号为 $y$ 的元素，则：

$n x t [y] = n x t [x]$ ， $n x t [x] = y$ .

注意 $n x t [y] = n x t [x]$ 必须在 $n x t [x] = y$ 之前执行.

有如下代码片段：

//代码片段-单向链表在编号为 x 的元素之后插入编号为 y 的元素
void add(int x, int y) {
	nxt[y] = nxt[x];
	nxt[x] = y;
}

单向链表一般没有在编号为 $x$ 的元素之前插入元素的需求.

带表头的单向链表如图1.1.7所示.

图1.1.7 带表头的单向链表

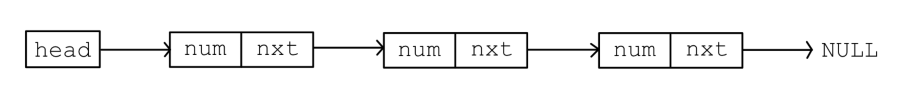
将编号为 $x$ 的元素插入到单向链表的开头，有：

$n x t [x] = h e a d$ ， $h e a d = x$ .

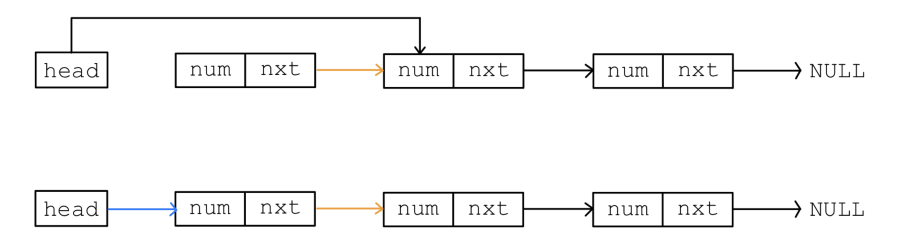
将元素插入在单向链表的开头如图1.1.8所示.

图1.1.8 将元素插入在单向链表的开头

有如下代码片段：

//代码片段-将元素插入在单向链表的开头
void add_head(int x) {
	nxt[x] = head;
	head = x;
}

类似的，这里直接给出删除双向链表开头元素的代码片段：

//代码片段-删除单向链表开头元素
void del_head(int x) {
	head = nxt[head];
}

从表头遍历链表*

设 $i$ 为当前遍历到的链表的元素的编号，则有：

链表中的第一个元素的编号即为 $h e a d$ ，故有 $i = h e a d$ ，并跳转到 2.
若 $i = - 1$ ，则说明链表已经遍历结束，退出遍历，否则跳转到 3.
现在遍历到了链表中编号为 $i$ 的元素，则对其进行一些操作后，访问下一个元素，即 $i = n x t [i]$ ，跳转到 2.

有如下代码片段：

//代码片段-从表头遍历链表
for (int i = head; i != -1; i = nxt[i]) {
	//do something...
}

对于单向链表，其基本功能有如下代码片段：

//将元素插入在单向链表的开头
void add_head(int x) {
	nxt[x] = head;
	head = x;
}
//删除单向链表开头元素
void del_head(int x) {
	head = nxt[head];
}
//删除单向链表中的元素
void del(int y) {
	nxt[y] = nxt[nxt[y]];
}
//单向链表在编号为 x 的元素之后插入编号为 y 的元素
void add(int x, int y) {
	nxt[y] = nxt[x];
	nxt[x] = y;
}

链表的优点与缺点

链表相较于数组的优点：

插入和删除元素比数组方便，数组删除中间某个元素需要将后继的元素进行移动，但链表只需要遍历到需要删除的元素删除即可.

链表相较于数组的缺点：

链表不能快速地访问随机一个元素，必须从表头开始遍历去访问.

习题

洛谷 P1160 队列安排

时间限制：1.00s　　内存限制：125.00MB

题目描述

一个学校里老师要将班上 $N$ 个同学排成一列，同学被编号为 $1\sim N$ ，他采取如下的方法：

先将 $1$ 号同学安排进队列，这时队列中只有他一个人；

$2\sim N$ 号同学依次入列，编号为 $i$ 的同学入列方式为：老师指定编号为 $i$ 的同学站在编号为 $1\sim(i-1)$ 中某位同学（即之前已经入列的同学）的左边或右边；

从队列中去掉 $M$ 个同学，其他同学位置顺序不变。

在所有同学按照上述方法队列排列完毕后，老师想知道从左到右所有同学的编号。

输入格式

第一行一个整数 $N$ ，表示了有 $N$ 个同学。

第 $2\sim N$ 行，第 $i$ 行包含两个整数 $k, p$ ，其中 $k$ 为小于 $i$ 的正整数， $p$ 为 $0$ 或者 $1$ 。若 $p$ 为 $0$ ，则表示将 $i$ 号同学插入到 $k$ 号同学的左边， $p$ 为 $1$ 则表示插入到右边。

第 $N + 1$ 行为一个整数 $M$ ，表示去掉的同学数目。

接下来 $M$ 行，每行一个正整数 $x$ ，表示将 $x$ 号同学从队列中移去，如果 $x$ 号同学已经不在队列中则忽略这一条指令。

输出格式

一行，包含最多 $N$ 个空格隔开的整数，表示了队列从左到右所有同学的编号。

样例输入
4
1 0
2 1
1 0
2
3
3
样例输出
2 4 1
样例解释

将同学 $2$ 插入至同学 $1$ 左边，此时队列为：2 1

将同学 $3$ 插入至同学 $2$ 右边，此时队列为：2 3 1

将同学 $4$ 插入至同学 $1$ 左边，此时队列为：2 3 4 1

将同学 $3$ 从队列中移出，此时队列为：2 4 1

同学 $3$ 已经不在队列中，忽略最后一条指令

最终队列：2 4 1

数据范围

对于 $20 %$ 的数据， $1\leq N\leq 10$ 。

对于 $40 %$ 的数据， $1\leq N\leq 1000$ 。

对于 $100\%$ 的数据， $1<M\leq N\leq 10^5$ 。

题解

使用双向链表模拟即可：
1. 先将 $1$ 号同学安排进队列，即建立一个有表头的空的双向链表后，将 1 号同学插入链表的开头.
2. $2 \sim N$ 号同学入队时，编号为 $i$ 的同学站在某位同学的左边（插入到其之前）或右边（插入到其之后）.
3. 从队列中去掉 $M$ 个同学，即为删除链表中的元素（注意有可能重复删除某个元素）.
最后输出队列时，直接从表头遍历链表即可.

代码

//洛谷P1160队列安排-双向链表写法
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int head = -1, nxt[N], pre[N];
void add_head(int x) {
	nxt[x] = head;
	pre[x] = -1;
	if (head != -1) pre[head] = x;
	head = x;
}
void add_L(int x, int y) {
	nxt[y] = x;
	pre[y] = pre[x];
	if (pre[x] == -1) head = y;
	else nxt[pre[x]] = y;
	pre[x] = y;
}
void add_R(int x, int y) {
	nxt[y] = nxt[x];
	pre[y] = x;
	if (nxt[x] != -1) pre[nxt[x]] = y;
	nxt[x] = y;
}
void del(int x) {
	if (pre[x] == -1)  head = nxt[x];
	else nxt[pre[x]] = nxt[x];
	if (nxt[x] != -1) pre[nxt[x]] = pre[x];
    nxt[x]=pre[x]=x; //本语句可以避免多次删除编号为 x 的元素引起的错误
}
int main() {
	int n; scanf("%d", &n);
	add_head(1);
	for (int i = 2; i <= n; ++i) {
		int k, p; scanf("%d%d", &k, &p);
		if (p == 0) add_L(k, i);
		else add_R(k, i);
	}
	int m; scanf("%d", &m);
	while (m--) {
		int x; scanf("%d", &x);
		del(x);
	}
	for (int i = head; i != -1; i = nxt[i])
		printf("%d ", i); // 链表的元素的编号即为人的编号，直接输出即可
	return 0;
}

时间复杂度分析

双向链表的操作的时间复杂度都是 $O (1)$ 的，遍历链表的时间复杂度为链表的长度，故本代码的时间复杂度为 $O (N)$ .

附件

//洛谷P1996约瑟夫问题-静态链表-先报数再判断出列的单向链表写法
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
int num[N], nxt[N];
int main() {
	int n, m; scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; ++i) {
		num[i] = i;
		nxt[i] = i + 1;
	}
	nxt[n] = 1;
	int now = n, pre, cnt = 0;
	/*
		now 为当前报数的人的编号
		pre 为上一个报数的人的编号
	*/
	while (n) {
		pre=now; now=nxt[now]; ++cnt;
		if(cnt==m){
			--n;
			printf("%d ",now);
			nxt[pre]=nxt[now];
			cnt=0;
		}
	}
	return 0;
}

//洛谷P1996约瑟夫问题-静态链表-使用结构体的双向链表写法
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
struct node{
	int nxt,pre;
}s[N];
int main() {
	int n, m; scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; ++i) {
		s[i].nxt=i+1;
		s[i].pre=i-1;
	}
	s[1].pre = n; s[n].nxt = 1;
	int now = n, pre, cnt = 0; 
	/*
		now 为当前报数的人的编号
		pre 为上一个报数的人的编号
	*/
	while (n) {
		pre=now; now=s[now].nxt; ++cnt;
		if(cnt==m){
			--n;
			printf("%d ", now);
			s[s[now].pre].nxt = s[now].nxt;
			s[s[now].nxt].pre = s[now].pre;
			cnt = 0; 
		}
	}
	return 0;
}

1.1.1 动态链表和 1.1.3 STL list 的内容很少在算法竞赛中涉及，在此忽略.↩
*：代表原书中并未涉及，内容为编者补充.↩

基础数据结构——1.1链表

基础数据结构——1.1链表

洛谷 P1996 约瑟夫问题

题目描述

输入格式

输出格式

样例输入

样例输出

提示

1.1.2 静态链表1

双向链表

构建双向链表

删除双向链表中的元素

代码实现

向双向链表中插入元素*2

表头和NULL*

将元素插入在双向链表的开头*

单向链表

构建单向链表

代码实现

向单向链表中插入元素*

从表头遍历链表*

链表的优点与缺点

习题

洛谷 P1160 队列安排

题目描述

输入格式

输出格式

样例输入

样例输出

样例解释

数据范围

题解

代码

附件

1.1.2 静态链表¹

向双向链表中插入元素*²

表头和`NULL`*