描述

题目描述

首先给我们了两个字符串，我们又三种操作分别是增删改，现在询问我们最少的操作次数，让两个字符串相同

样例解释

假设我们的两个字符串分别是

"nawcoder","nowcoder"

这里我们只需要把$a\mathrm{改}\mathrm{成}oa改成o$就可以得到第二个字符串，所以操作数是$11$

所以我们的输出是

1

对三种情况的方式判断

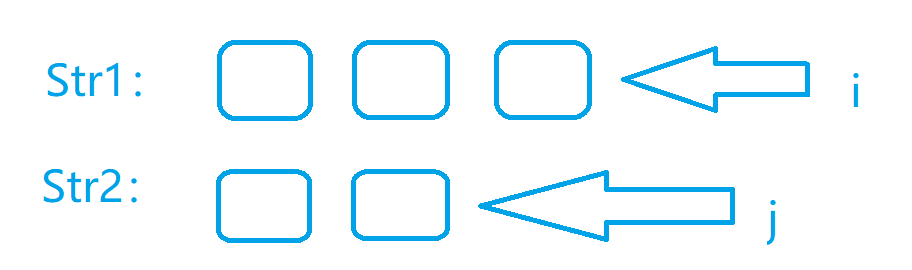
假设我们这种情况就是我们遍历我们的两个字符串分别到了第$ii$位和第$jj$位，现在我们进行判断

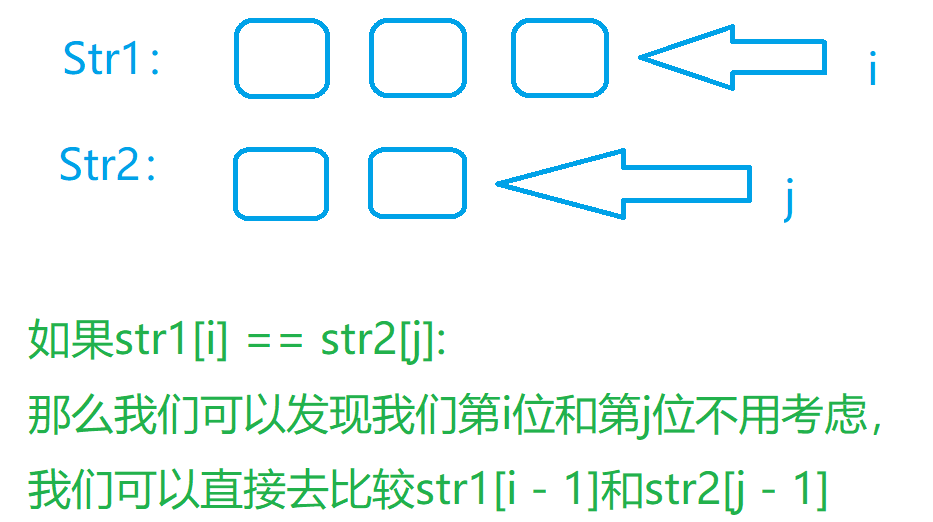
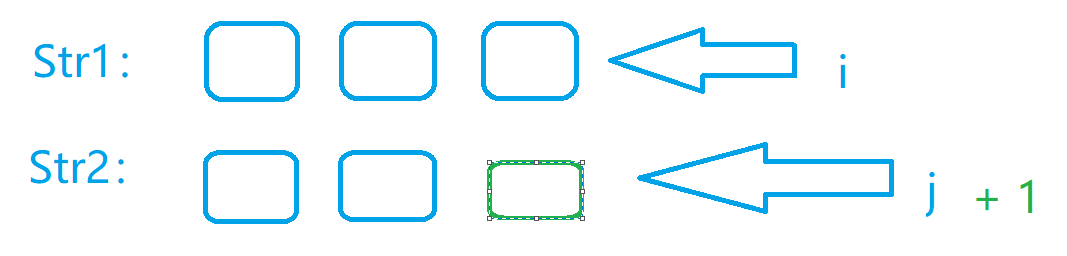
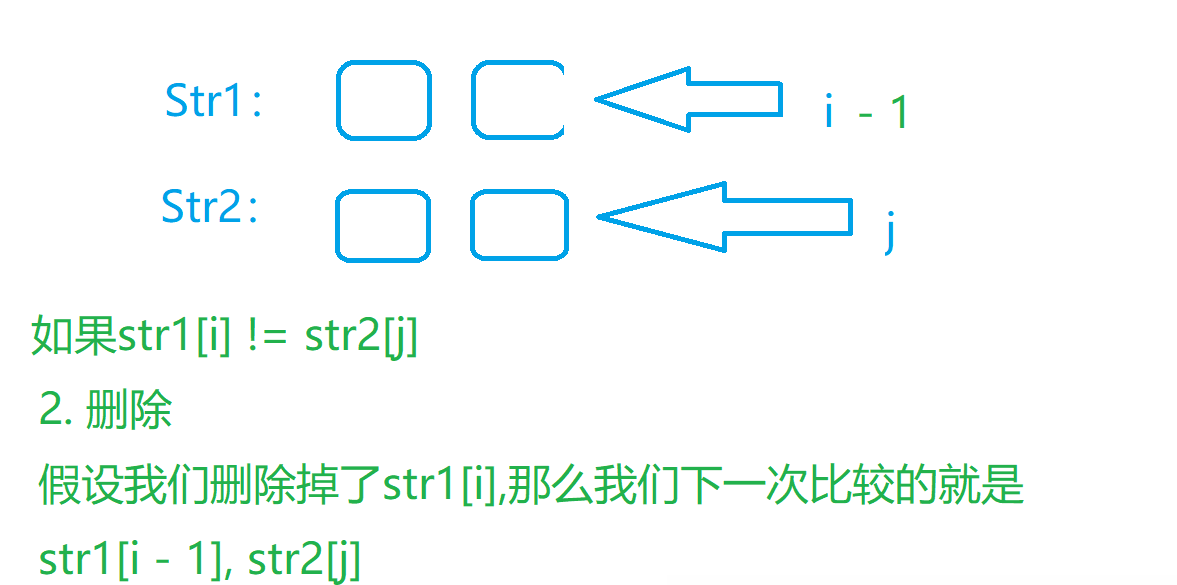
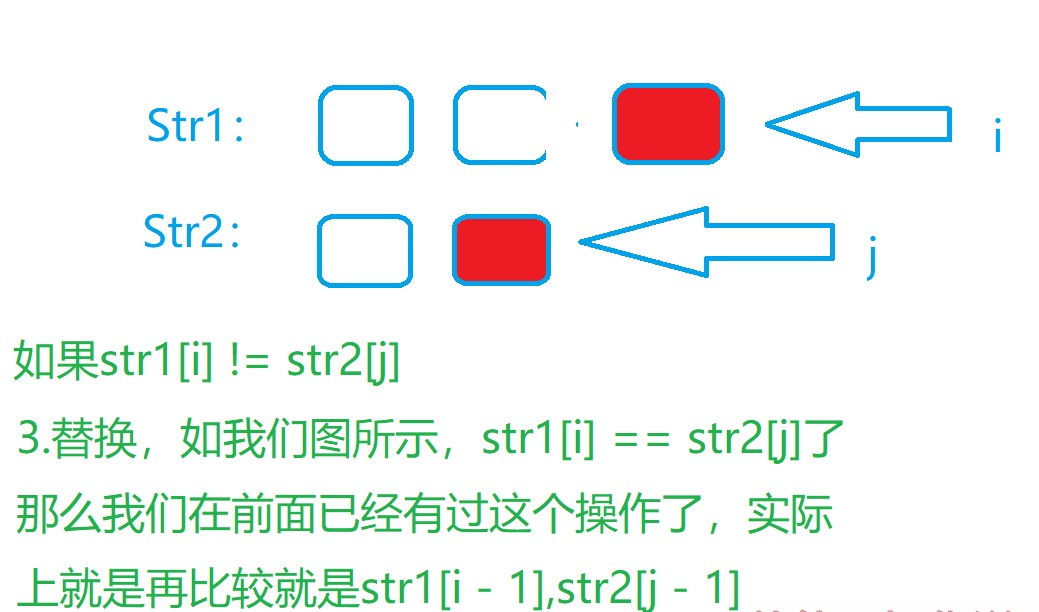
题解

解法一：DFS + 记忆化

解题思路

这里我们采用自顶向下的方式，我们如果直接暴力DFS，那么我们的复杂度是$O(2^n)O(2\; ^\; n)$的，这个显然是我们无法接受的，那么我们可以想到，把我们计算过的情况用一个二维数组存下来，比如$vis[i][j]vis[i][j]$代表的就是我们到了$str1\mathrm{的}\mathrm{第}i\mathrm{位}\mathrm{和}str2\mathrm{的}\mathrm{第}j\mathrm{位}str1的第i位和str2的第j位$，这样我们每次进行dfs判断，首先确定递归的终点，

1. 第一个就是我们之前计算过，可以直接返回
2. 第二个如果两个位置相等，我们可以直接记录返回
3. 第三个如果有一个走到了头，遍历完字符串的所有位置了，我们返回
4. 最后就是判断当前的位置，增删改这三种操作，哪一种操作的代价更小，然后因为我们肯定会操作，所以最小的代价 + 我们操作的一次

代码实现

#include <bits/stdc++.h>

using namespace std;

class Solution {
    int vis[1010][1010];

   public:
    int dfs(string s1, int i, string s2, int j) {
        if (vis[i][j] != -1) return vis[i][j];
        //         如果这位已经计算过了
        if (i == s1.size()) return vis[i][j] = s2.size() - j;
        //         如果我们的s1字符串已经到了结尾，我们只需要删操作s2就可以了
        if (j == s2.size()) return vis[i][j] = s1.size() - i;
        //         s2到了结尾
        if (s1[i] == s2[j]) return vis[i][j] = dfs(s1, i + 1, s2, j + 1);
        //         当我们发现现在的两个字符串的最后一位是一样的,我们可以直接当成这两位没有,进行下一次操作
        return vis[i][j] =
                   min(dfs(s1, i + 1, s2, j + 1),
                       min((dfs(s1, i + 1, s2, j)), (dfs(s1, i, s2, j + 1)))) +
                   1;
        //         找到我们三种操作的最小的情况
    }
    int editDistance(string str1, string str2) {
        memset(vis, -1, sizeof vis);
        return dfs(str1, 0, str2, 0);
    }
};
signed main() {
    string s1, s2;
    cin >> s1 >> s2;
    Solution s;
    cout << s.editDistance(s1, s2) << "\n";
    return 0;
}

时空复杂度分析

时间复杂度： $O(n^2)O(n\; ^\; 2)$

理由如下，遍历两个字符串的所有位置

空间复杂度： $O(n^2)O(n\; ^\; 2)$

理由如下，开辟了$n\ast nn\; *\; n$的记忆化数组

解法二：动态规划

解题思路

我们这里其实也是这么几种情况

$dp[i][j]dp[i][j]$表示为从$str1\mathrm{的}\mathrm{第}i\mathrm{位}\mathrm{变}\mathrm{化}\mathrm{位}str2\mathrm{的}\mathrm{第}j\mathrm{位}str1的第i位变化位str2的第j位$次数

1. $str1\mathrm{第}i\mathrm{位}\mathrm{和}str2\mathrm{第}j\mathrm{位}\mathrm{一}\mathrm{样}str1第i位和str2第j位一样$ $dp[i][j]=dp[i-1][j-1]dp[i][j]\; =\; dp[i\; -\; 1][j\; -\; 1]$

2. $str1\mathrm{第}i\mathrm{位}\mathrm{和}str2\mathrm{第}j\mathrm{位}\mathrm{不}\mathrm{一}\mathrm{样}str1第i位和str2第j位不一样$ $dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1dp[i][j]\; =\; min(dp[i\; -\; 1][j\; -\; 1],\; dp[i\; -\; 1][j],\; dp[i][j\; -\; 1])\; +\; 1$

这个就是我们的状态转移方程

代码实现

#include <bits/stdc++.h>

using namespace std;

class Solution {
   public:
    int editDistance(string str1, string str2) {
        int len1 = str1.size(), len2 = str2.size();
        vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));
        //         创建DP数组
        for (int i = 1; i <= len1; i++) dp[i][0] = dp[i - 1][0] + 1;
        for (int i = 1; i <= len2; i++) dp[0][i] = dp[0][i - 1] + 1;
        //         DP数组的初始化
        for (int i = 1; i <= len1; i++)
            for (int j = 1; j <= len2; j++)
                if (str1[i - 1] == str2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] =
                        min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) +
                        1;
        //         我们在之前推导出来的状态转移方程
        return dp[len1][len2];
    }
};
signed main() {
    string s1, s2;
    cin >> s1 >> s2;
    Solution s;
    cout << s.editDistance(s1, s2) << "\n";
    return 0;
}

时空复杂度分析

时间复杂度： $O(n^2)O(n\; ^\; 2)$

理由如下，遍历两个字符串的所有位置

空间复杂度： $O(n^2)O(n\; ^\; 2)$

理由如下，开辟了$n\ast nn\; *\; n$的记忆化数组

区别

其实我们记忆化搜索和我们的动态规划在某些题目中，其实区别就是一个自顶向下，一个自自向上