1. 投影

向量 b = ( 2 , 3 , 4 ) b = (2, 3, 4) b=(2,3,4) 在 z z z 轴上和在 x y xy xy 平面上的投影是什么，哪个矩阵能产生到一条线上和到一个平面的投影？

当 b b b 被投影到 z z z 轴上时，它的投影 p p p 就是 b b b 沿着那条线的部分。当 b b b 被投影到一个平面时，它的投影就是 b b b 在平面中的部分。

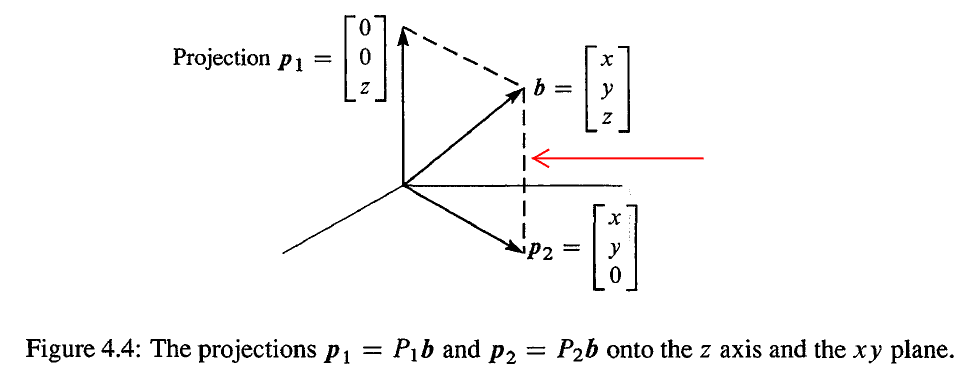
到 z z z 轴上的投影 p 1 = ( 0 , 0 , 4 ) p_1 = (0, 0, 4) p1​=(0,0,4)，到 x y xy xy 平面上的投影 p 2 = ( 2 , 3 , 0 ) p_2 = (2, 3, 0) p2​=(2,3,0)，两个投影矩阵 P 1 P_1 P1​ 和 P 2 P_2 P2​ 分别为

P 1 P_1 P1​ 就是选出每个向量的 z z z 分量， P 2 P_2 P2​ 就是选出每个向量的 x x x 和 y y y 分量。

在这个例子中， z z z 轴和 x y xy xy 平面是正交子空间，就像地面和两面墙的交线一样。

除此之外，它们还是正交补的。整个空间的任意向量都可以表示为它们在两个子空间中分量的和。

2. 到一条线上的投影

假设一条过原点的直线方向为 a = ( a 1 , a 2 , ⋯   , a m ) a = (a_1, a_2,\cdots, a_m) a=(a1​,a2​,⋯,am​)，我们要将点 b = ( b 1 , b 2 , ⋯   , b m ) b = (b_1, b_2,\cdots, b_m) b=(b1​,b2​,⋯,bm​) 投影到这条直线上。

投影 p p p 和 a a a 在一条直线上，因此有 p = <mover accent="true"> x ^ </mover> a p = \hat xa p=x^a，误差 e = b − p = b − <mover accent="true"> x ^ </mover> a e = b-p = b-\hat xa e=b−p=b−x^a，然后由 e e e 垂直于 a a a，我们可得。

e ⋅ a = 0 → ( b − <mover accent="true"> x ^ </mover> a ) ⋅ a = 0 → a ⋅ b − <mover accent="true"> x ^ </mover> a ⋅ a = 0 e \cdot a = 0 \to (b-\hat xa) \cdot a = 0 \to a\cdot b - \hat x a\cdot a = 0 e⋅a=0→(b−x^a)⋅a=0→a⋅b−x^a⋅a=0

因此，可求得系数 <mover accent="true"> x ^ </mover> \hat x x^ 为

<mover accent="true"> x ^ </mover> = a ⋅ b a ⋅ a = a T b a T a \hat x = \frac{a\cdot b}{a\cdot a} = \frac{a^Tb}{a^Ta} x^=a⋅aa⋅b​=aTaaTb​

投影为 p = <mover accent="true"> x ^ </mover> a = a T b a T a a p = \hat x a = \frac{a^Tb}{a^Ta} a p=x^a=aTaaTb​a。

如果 b = a b=a b=a，那么 <mover accent="true"> x ^ </mover> = 1 \hat x = 1 x^=1，投影还是它自己， P a = a Pa = a Pa=a。 如果 b ⊥ a b\perp a b⊥a，那么 <mover accent="true"> x ^ </mover> = 0 \hat x = 0 x^=0，投影为 0。

将投影重写为 p = a <mover accent="true"> x ^ </mover> = a a T b a T a = a a T a T a b p = a \hat x =a \frac{a^Tb}{a^Ta} = \frac{aa^T}{a^Ta}b p=ax^=aaTaaTb​=aTaaaT​b。因此，投影矩阵 P = a a T a T a P = \frac{aa^T}{a^Ta} P=aTaaaT​。

如果向量 a a a 变为两倍，投影矩阵 P P P 不变，它还是投影到同一条直线。如果投影矩阵平方，那就是进行两次投影，和进行一次投影是一样的结果，因此有 P 2 = P P^2=P P2=P。

同时， I − P I-P I−P 也是一个投影矩阵， ( I − P ) b = b − p = e (I-P)b = b-p = e (I−P)b=b−p=e。当 P P P 投影到一个子空间时， I − P I-P I−P 投影到和它垂直的另一个子空间。

3. 到子空间的投影

假设 n n n 个 R m \boldsymbol R^m Rm 空间中的向量 a 1 , ⋯ &ThinSpace; , a n a_1,\cdots,a_n a1​,⋯,an​ 是线性不相关的，我们想找到一个线性组合 p = <mover accent="true"> x ^ </mover> 1 a 1 + ⋯ + <mover accent="true"> x ^ </mover> n a n p=\hat x_1 a_1+\cdots+\hat x_n a_n p=x^1​a1​+⋯+x^n​an​ 使得 p p p 距离一个给定向量 b b b 最近。

a 1 , ⋯ &ThinSpace; , a n a_1,\cdots,a_n a1​,⋯,an​ 可以看做是矩阵 A A A 的列，我们要找的线性组合是在矩阵 A A A 的列空间中。我们要找的是距离 b b b 最近的一个组合 A <mover accent="true"> x ^ </mover> A\hat x Ax^，也就是 b b b 在列空间的投影。

同理，误差 e = b − A <mover accent="true"> x ^ </mover> e=b-A\hat x e=b−Ax^ 垂直于子空间，也就是垂直于子空间的所有向量。

也即

A T ( b − A <mover accent="true"> x ^ </mover> ) = 0 → A T A <mover accent="true"> x ^ </mover> = A T b A^T(b-A\hat x) = 0 \to A^TA\hat x = A^Tb AT(b−Ax^)=0→ATAx^=ATb

A T A A^TA ATA 是一个 n×n 的矩阵，因为 A A A 的列是线性不相关的，所以其是可逆的。可得线性组合系数为

<mover accent="true"> x ^ </mover> = ( A T A ) − 1 A T b \hat x = (A^TA)^{-1}A^Tb x^=(ATA)−1ATb

所以有，投影和投影矩阵分别为

p = A <mover accent="true"> x ^ </mover> = A ( A T A ) − 1 A T b p = A \hat x = A(A^TA)^{-1}A^Tb p=Ax^=A(ATA)−1ATb

P = A ( A T A ) − 1 A T P = A(A^TA)^{-1}A^T P=A(ATA)−1AT

由 A T ( b − A <mover accent="true"> x ^ </mover> ) = 0 A^T(b-A\hat x) = 0 AT(b−Ax^)=0 可知，误差 e e e 位于 A A A 的左零空间 N ( A T ) N(A^T) N(AT) 中，向量 b b b 被分为了投影 p p p 和误差 e e e 两部分。

A T A A^TA ATA 是可逆的当且仅当 A A A 的列是线性不相关的。

当 A x = 0 Ax=0 Ax=0 时，我们有 A T A x = 0 A^TAx=0 ATAx=0。而当 A T A x = 0 A^TAx=0 ATAx=0 时，我们有
x T A T A x = 0 → ( A x ) T A x = 0 → A x = 0 x^TA^TAx=0 \to (Ax)^TAx = 0 \to Ax = 0 xTATAx=0→(Ax)TAx=0→Ax=0

因此 A T A A^TA ATA 和 A A A 有着一样的零空间，当 A A A 的列线性不相关时， A T A A^TA ATA 是一个方阵，对称并且可逆。

获取更多精彩，请关注「seniusen」!