文章目录

题目链接：

51nod 1642
cf594D

cf上竟然有405ms的（惊恐.jpg）
【快速单次取逆元】
学习了一个单次快速取模的代码，不懂啥意思T_T：

LL inv(int x)
{
  LL r = 1;
  for (; x > 1; x = MOD % x)
    r = r * LL(-MOD/x) % MOD;
  return (r+MOD)%MOD;
}

题意：给N个数，Q次询问[qL,qR]内所有数乘积的欧拉函数

因为是求欧拉函数，所以只用统计区间内有多少有哪些质因子就阔以计算出欧拉函数了
可是怎么统计喃？1e6以内的质数有70000+个，每个质数建个数据结构来区间统计，那空间不是炸了嘛，于是我便没了思路

题解的意思大概是直接统计有影响的因子的欧拉那一部分
比如2 3 4的欧拉值
2 ⋅ 3 ⋅ 4 ⋅ ( 1 − 1 2 ) ⋅ ( 1 − 1 3 ) 2\cdot3\cdot4\cdot(1-\frac{1}{2})\cdot(1-\frac{1}{3}) 2⋅3⋅4⋅(1−21​)⋅(1−31​)
我们就统计后面括号里的

但是这样只能得到[1,qR]的答案，还没有[L,R]=[1,R]-[1,L-1]这个性质怎么办喃？

sy的思路

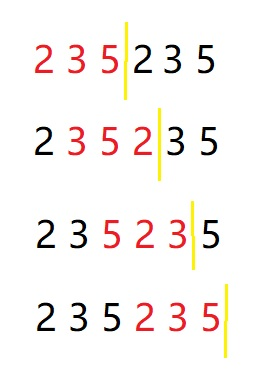
把每个询问按照左端点升序排列，对于每一个询问[qL,qR]，我们把前缀里的有贡献的因子都弄到 [qL,qR] 里面，这样就能够满足L,R]=[1,R]-[1,L-1]这个性质了
他这个思路想当于是把当前这个因子复制到后面去，所以要预处理出每个因子后面会在哪里出现，而其他博客的是把因子从前面那个位置挪过来，就直接记录前面是在哪个位置就行了不用预处理

/*宋毅的写法*/
#include"bits/stdc++.h"
//#define inv(n) ksm(n,MOD-2,MOD)
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
const int MOD=1e9+7;
LL ksm(LL a,LL b,LL mod)
{
	LL res=1,base=a;
	while(b)
	{
		if(b&1)res=(res*base)%mod;
		base=(base*base)%mod;
		b>>=1;
	}
	return res;
}
LL inv(int x)
{
  LL r = 1;
  for (; x > 1; x = MOD % x)
    r = r * LL(-MOD/x) % MOD;
  return (r+MOD)%MOD;
}
vector<int>factor[maxn];
void PHI(int n)
{
	static vector<int>prime;
	static bool vis[maxn];
	/*处理质数*/
	memset(vis,1,sizeof(vis));
	for(int i=2; i<=n; i++)
	{
		if(vis[i])prime.push_back(i);
		for(int j=0; j<prime.size()&&i*prime[j]<=n; j++)
		{
			vis[i*prime[j]]=0;
			if(i%prime[j]==0)break;
		}
	}
	/*筛每个数的质因子，只要质因子*/
	for(int i=0; i<prime.size(); i++)
	{
		for(int k=1; k*prime[i]<=n; k++) //枚举质因子pirme[i]的倍数，质因子的倍数是肯定包含质因子的
		{
			factor[k*prime[i]].push_back(prime[i]);
		}
	}
}
int N,Q;
LL a[maxn],sum[maxn]= {1};
struct AAA
{
	int L,R,id;
	bool operator<(const AAA &tp)const
	{
		return L<tp.L;
	}
};
AAA q[maxn];
LL tree[maxn];
void Add(int i,LL val)
{
	if(i<1)return ;
	for(; i<=N; i+=i&-i)tree[i]=(tree[i]*val)%MOD;
}
LL getsum(int i)
{
	LL res=1;
	for(; i>=1; i-=i&-i)res=(res*tree[i])%MOD;
	return res;
}
int RR[maxn][20];//RR[i][j]表示第i个数的第j个因子p下一次出现在哪里 
void PreSolve()//预处理出这个因子的下一次出现的位置 
{
	static int flag[maxn];
	for(int i=0;i<maxn;i++)flag[i]=N+1;
	for(int i=N;i>=1;i--)
	{
		int t=a[i];
		for(int j=0;j<factor[t].size();j++)
		{
			int p=factor[t][j];
			RR[i][j]=flag[p];//在所有因子中取最左边的 
			flag[p]=i;//p这个质因子的位置更新成i 
		}
	}
}
int main()
{
	PHI(maxn-5);
	while(cin>>N)
	{
		for(int i=0; i<maxn; i++)tree[i]=1;
		for(int i=1; i<=N; i++)
		{
			scanf("%lld",a+i);
			sum[i]=sum[i-1]*a[i]%MOD;
		}
		PreSolve();
		cin>>Q;
		for(int i=1; i<=Q; i++)
		{
			scanf("%d%d",&q[i].L,&q[i].R);
			q[i].id=i;
		}
		sort(q+1,q+1+Q);
		static int ans[maxn];
		static bool vis[maxn];//vis[p]表示p这个因子出没出现过 
		memset(vis,0,sizeof vis);
		int L=1,R=1;
		for(int i=1;i<=Q;i++)
		{
			int qL=q[i].L,qR=q[i].R,id=q[i].id;
			while(R<=qR)
			{
				int t=a[R];
				for(int j=0;j<factor[t].size();j++)
				{
					int p=factor[t][j];
					if(vis[p]==0)
					{
						Add(R,(LL)(p-1)*inv(p)%MOD);//如果p这个因子没出现过，就把p的影响加进去 
						vis[p]=1;
					}
				}
				R++;
			}
			while(L<qL)
			{
				int t=a[L];
				for(int j=0;j<factor[t].size();j++)
				{
					int p=factor[t][j];
					Add(RR[L][j],(LL)(p-1)*inv(p)%MOD);//p这个因子赋值到下一次出现p这个因子的地方 
				}
				L++;
			}
			ans[id]=sum[qR]*inv(sum[qL-1])%MOD*getsum(qR)%MOD*inv(getsum(qL-1))%MOD;
		}
		for(int i=1; i<=Q; i++)printf("%d\n",ans[i]);
	}
}

网上博客的思路

这里一个非常巧妙的做法就是，对于有贡献的那个因子，我们用最靠近 qR 的那个因子来计算贡献

比如要求到黄线那里的欧拉值，出现过的因子只取最近的那一个，这样就能满足[L,R]=[1,R]-[1,L-1]这个性质了
但是因为有个挪动的操作，就多了一个减法操作，因此这个的代码差不多是上面的2倍时间，虽然也能AC，随机生成了个满的数据跑了4000+ms，上面的只跑了2000+ms

#include"bits/stdc++.h"
#define inv(n) ksm(n,MOD-2,MOD)
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
const int MOD=1e9+7;
LL ksm(LL a,LL b,LL mod)
{
	LL res=1,base=a;
	while(b)
	{
		if(b&1)res=(res*base)%mod;
		base=(base*base)%mod;
		b>>=1;
	}
	return res;
}
vector<LL>prime;
bool vis[maxn];
vector<int>factor[maxn];
void PHI(int n)
{
	/*处理质数*/
	memset(vis,1,sizeof(vis));
	for(int i=2; i<=n; i++)
	{
		if(vis[i])prime.push_back(i);
		for(int j=0; j<prime.size()&&i*prime[j]<=n; j++)
		{
			vis[i*prime[j]]=0;
			if(i%prime[j]==0)break;
		}
	}
	/*筛每个数的质因子，只要质因子*/
	for(int i=0;i<prime.size();i++)
	{
		for(int k=1;k*prime[i]<=n;k++)//枚举质因子pirme[i]的倍数，质因子的倍数是肯定包含质因子的 
		{
			factor[k*prime[i]].push_back(prime[i]);
		}
	}
}
int N,Q;
LL a[maxn],sum[maxn]= {1};
struct AAA
{
	int L,R,id;
	bool operator<(const AAA &tp)const
	{
		return R<tp.R;
	}
};
AAA q[maxn];
LL tree[maxn];
void Add(int i,LL val)
{
	if(i<1)return ;
	for(; i<=N; i+=i&-i)tree[i]=(tree[i]*val)%MOD;
}
LL getsum(int i)
{
	LL res=1;
	for(; i>=1; i-=i&-i)res=(res*tree[i])%MOD;
	return res;
}
int main()
{
	PHI(maxn-5);
	while(cin>>N)
	{
		for(int i=0; i<maxn; i++)tree[i]=1;
		for(int i=1; i<=N; i++)
		{
			scanf("%lld",a+i);
			sum[i]=sum[i-1]*a[i]%MOD;
		}
		cin>>Q;
		for(int i=1; i<=Q; i++)
		{
			scanf("%d%d",&q[i].L,&q[i].R);
			q[i].id=i;
		}
		sort(q+1,q+1+Q);
		static int last[maxn];//last[p]表示p这个因子上次在哪个位置
		memset(last,0,sizeof last);
		static int ans[maxn];
		int now=1;//表示第now个询问区间
		for(int i=1; i<=N; i++)
		{
			for(int j=0; j<factor[a[i]].size(); j++)
			{
				LL p=factor[a[i]][j];
				if(last[p])Add(last[p],p*inv(p-1)%MOD);//把上个位置上的因子p的影响取消了
				Add(i,(LL)(p-1)*inv(p)%MOD);//在这个位置上加上p这个因子的影响
				last[p]=i;
			}
			while(q[now].R==i)
			{
				int id=q[now].id;
				int qL=q[now].L;
				ans[id]=sum[i]*inv(sum[qL-1])%MOD*getsum(i)%MOD*inv(getsum(qL-1))%MOD;
				now++;
			}
		}
		for(int i=1; i<=Q; i++)printf("%d\n",ans[i]);
	}
}