2009提高组初赛讲解

2009NOIP提高组初赛

题解 – by L_Y_T

一.单项选择题

1.C

A.世界上最早的计算机是1946年美国的ENIAC

B&C&D.1936年,图灵提出了一种新的计算模型—图灵机

2.A

BIOS <==> “Basic Input Output System” ,基本输入输出系统

3.D

j的二进制编码为 $(74{)}_{10}$(74)10​ = $(4A{)}_{16}$(4A)16​

$\frac{74}{16}$1674​ = 4 … 10 , $\frac{4}{16}$164​ = 0 … 4 , 所以16进制就是4 10(A) 了

4.B

来下定义:

原码:在用二进制原码表示的数中 ， 符号位为0 表示正数 ， 符号位为1 表示负数 ，
其余各位表示数值部分 .

反码:反码的定义如下 :
⑴ 对于正数，它的反码表示与原码相同。即 $x_{反}$x反​ = $x_{原}$x原​
⑵对于负数，则除符号位仍为“ 1” 外，其余各位“ 1” 换成” 0” ，**” 0” 换成1” **，即得到反码 [X] 反。例如 $-1101001_{反}$−1101001反​=10010110 。

(3)对于0, $0_{反}$0反​有两种表示: $+0_{反}$+0反​=000…0 , $-0_{反}$−0反​ = 111…1 ;

补码:正数的补码就是该数本身

即 : $[01100100{]}_{补}$[01100100]补​ = 01100100

负数:两头的1不变,中间取反

当然,你也可以用这个结论 $[x{]}_{补}=[x{]}_{反}+1$[x]补​=[x]反​+1

即: $[10100100{]}_{补}$[10100100]补​ == 11011100

嗯…有一点注意一下:0只有一个补数

由补码的定义可知: $(1111111111101101{)}_2$(1111111111101101)2​ 与其10进制真值的关系为 $2^{16} + X = (1111111111101101)_2 $ ,解得: $X=-(2^{16}-(1111111111101101{)}_2$X=−(216−(1111111111101101)2​ = $-(65536-65517)=-19$−(65536−65517)=−19 .

5.m层满k二叉树有 $\frac{1-k^m}{1-k}$1−k1−km​ 个节点,非叶节点有 $k^{m-1}$km−1个,叶节点有 $k^{m-1}$km−1 个, $k^{m-1}$km−1 = $k^{m-1}=\frac{1-k^{m-1}}{1-k}\ast (k-1)+1$km−1=1−k1−km−1​∗(k−1)+1

6.后缀表达式的主要特点是左右根,根节点有表示符号,左右两边石狮子或数字

表达式有前缀表达式,中缀表达式和后缀表达式

中缀表达式就是我们平常看的式子:举个栗子: $(3+4)\ast 5-6$(3+4)∗5−6 就是最普通的式子

前缀表达式:运算符在操作数之前

我们把上面的式子转一下:

将中缀表达式转换为前缀表达式步骤：
讲解

(1) 初始化两个栈：运算符栈 $S_1$S1​和储存中间结果的栈 $S_2$S2​；

(2) 从右至左扫描中缀表达式；

(3) 遇到操作数时，将其压入 $S_2$S2​；

(4) 遇到运算符时，比较其与 $S_1$S1​栈顶运算符的优先级：

( $4_1$41​) 如果 $S_1$S1​为空，或栈顶运算符为右括号“)”，则直接将此运算符入栈；

(4 $2_{}$2​) 否则，若优先级比栈顶运算符的较高或相等，也将运算符压入 $S_1$S1​；

( $4_3$43​) 否则，将 $S_1$S1​栈顶的运算符弹出并压入到 $S_2$S2​中，再次转到( $4_1$41​)与 $S_1$S1​中新的栈顶运算符相比较；

(5) 遇到括号时：

( $5_1$51​) 如果是右括号“)”，则直接压入 $S_1$S1​；

( $5_2$52​) 如果是左括号“(”，则依次弹出 $S_1$S1​栈顶的运算符，并压入 $S_2$S2​，直到遇到右括号为止，此时将这一对括号丢弃；

(6) 重复步骤(2)至(5)，直到表达式的最左边；

(7) 将 $S_1$S1​中剩余的运算符依次弹出并压入 $S_2$S2​；

(8) 依次弹出S2中的元素并输出，结果即为中缀表达式对应的前缀表达式。

7.B

Huffman编码不允许一个编码是另一个的前缀

8.A

这道题硬将也不行吧

9.A

prim算法是指从起点开始,每次找与当前节点距离最短的节点进行扩展,已经被扩展的节点不在扩展

然而,我是直接看的克鲁斯卡尔…所以prim我并不会

10.C

NOI官网

二.不定项选择

11.AB
Intel最早发明的是微处理器,位数只能说明处理的字长,所在的系统硬件不同,速度很难说谁快.
12.BD
RAM的位置不是随机,而是随时访问.高速缓存和寄存器的物理实现是集成在CPU中.
13.BC
多任务系统可以是单个CPU构架的,普通的PC都是多任务的.而且操作系统不是都是免费的.
14.C
网络协议分层不是为了兼容,而是根据网络的分层模型来的.新的IPv6是IPv4的升级.必须要有IP地址才能进入互联网.
15.BD
HTML没有统一编码.本网站页面间也可以用超链接.
16.ABD
画个图就看出来了…嗯?!不用我画吧!!..算了,我还是一画吧!!..

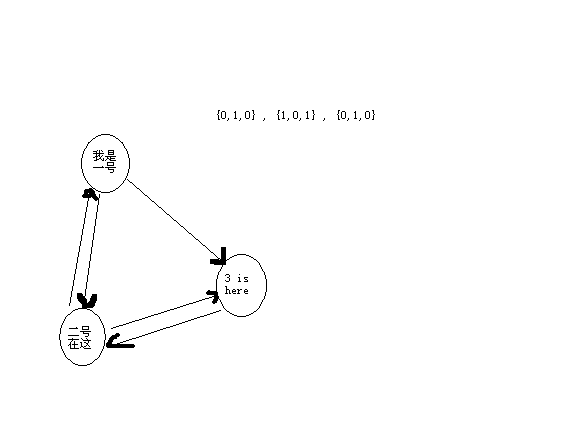
手绘图…说实话怪丑
但是可以判断,ABD是对的,C是错的了吧…
17.AC
链表的常识题…
不会的话自己动手试试也行了…
18.ABC
按照题意,求出26%11=4(这里的’='不是赋值) ,以此类推,得出那几个数求出的"散列值"为4,3,6,5,8,7,4 . 5有可能为26,59. 7可能为36,38,72,59. 9有可能为26,38,72,18,8,59.
19.ABCD
希尔排序,快排,直接选择排序,堆排都是不问定的
20.ACD
嗯…我咋感觉B项挺好的啊…

三.问题求解

1.432
可以看出有两个DAG.(把图片插过来先)

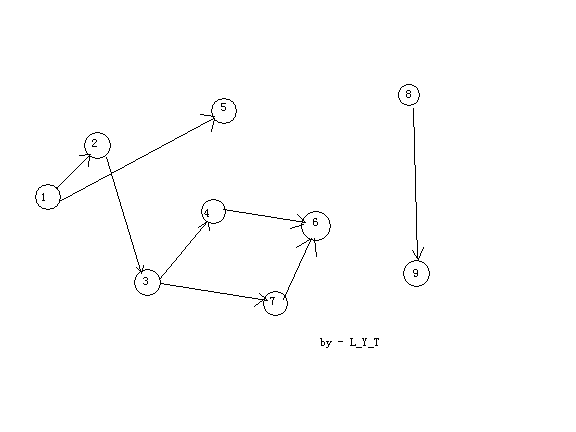
1一定是序列的第一个点,接下来是2和5,因为5后面没有连接的数字,所以们先考虑2.然后是3,然后是4(或7),6要在4和7后,根据乘法原理1,2,3,4,6,7,只有2中派发,分别是 $1,2,3,4,7,6$1,2,3,4,7,6和 $1,2,3,7,4,6$1,2,3,7,4,6 吧5排在1的后面,共有6个位置,则有 $2\ast 6=12$2∗6=12 中.再讲8和9插入其***有 ${\sum }_{i=1}^{n=8}i种情况$∑i=1n=8​i种情况
原因嘛…画个图就知道了…但我不想画
所以,共有1236=432
2.35
10015化成7进制是 $(41125{)}_7$(41125)7​,正常是47+1=29张 $7^3$73面额的,1张 $7^2$72面额的,和2张 $7^1$71面额的,以及5张 $7^0$70面额的~~(我有毒吧)~~.这样,我们可以找数值大于4的,并用7-a的方法来找零这样,总数就是29+2+1+(1+7-5)=35张.

阅读程序

1.这道题是一道gcd

2.模拟.tmp = 1 时,a,b的数组的值分别为2,5,26,92和94,8,49,33.然后将每一位的各位相加后再相乘.

3.求杨辉三角的第n行. $c\left[i\right]\left[j\right]=c[i-1][j-1]+c[i-1]\left[j\right]$c[i][j]=c[i−1][j−1]+c[i−1][j]

4.将分数化为小数.

ans : 3 , 5850 , 487 , 0.(384615)

完善程序

只提供答案
1.
(1) 0
(2) ans == tmp + a[i]
(3) <0
(4) i
(5) tmp += a[i]
2.
(1) now <= maxnum
(2) second - first
(3) (ans - 1)
(4) hash[first] >= ans
(5) ok
(6) work(0)
PS:答案不唯一(当然也有唯一的)