杭电多校第一场 1007 Chiaki Sequence Revisited
1007 Chiaki Sequence Revisited
题意
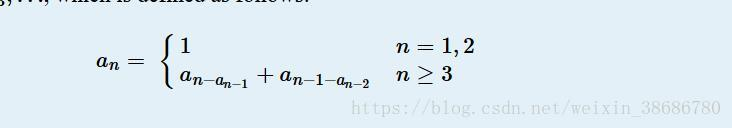
给定 的递推式,求 的前缀和
打表
1 1
2 2
3
4 4 4
5
6 6
78 8 8 8
9
10 10
11 12 12 12
13
14 14
15
16 16 16 16 16
我们设数字i出现的次数 为
观察到规律,每一个数出现的次数是该数里含2的因子数的个数+1,转化成数学语言就是
如果有
那么有
唯一例外的就是1,排除掉这个就行了
那么从 1,…n 出现次数总和是多少呢
设为g(n)
// 注意是整除
这个概念和阶乘尾零的求法很相似
例如 n = 8 的时候
| n/ | i | 个数 |
|---|---|---|
| n = 8 | 1 2 3 4 5 6 7 8 | 8个数字算一次 |
| n/2 = 4 | 2 4 6 8 | 4个数字算二次 |
| n/4 = 2 | 4 8 | 2个数字算三次 |
| n/8 = 1 | 8 | 1个数字算四次 |
| 出现次数 | 1 2 1 3 1 2 1 4 | 15 |
好了我们知道这个规律之后就可以求得 的值了,方法就是二分枚举 的值,如果有 则必有
如果知道 的值之后怎么求前缀和呢
求前缀和
所以问题转化成了 如何求
我们又知道 每个数出现的次数
所以
举例说明
1 2 3 4 5 6 7 8 求和一次
2 4 6 8 求和一次是
4 8 求和是 ;
代码如下
#include <bits/stdc++.h>
#define mem(ar,num) memset(ar,num,sizeof(ar))
#define me(ar) memset(ar,0,sizeof(ar))
#define lowbit(x) (x&(-x))
#define Pb push_back
#define FI first
#define SE second
#define For(i,a,b) for(int i = a; i < b; ++i)
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int prime = 999983;
const int INF = 0x7FFFFFFF;
const LL INFF =0x7FFFFFFFFFFFFFFF;
const double pi = acos(-1.0);
const double inf = 1e18;
const double eps = 1e-6;
const LL mod = 1e9 + 7;
int dr[2][4] = {1,-1,0,0,0,0,-1,1};
typedef pair<int,int> P;
LL n;
bool judge(LL mid,LL n){
LL ans = 0;
while(mid > 0)
ans += mid,mid >>= 1;
return ans >= n;
}
const LL inv2 = 500000004;
const int maxn = 1e6;
LL a[maxn];
LL an[maxn];
LL F(LL n){
if(n < 200){
return a[n];
}
n--;
LL l = 1,r = n;
while(r >= l){
LL mid = l+((r-l)>>1);
if(!judge(mid,n))
l = mid+1;
else
r = mid-1;
}
LL ans = 0;
LL num = 0;
while( r > 0)
num += r, r >>=1;
num = n-num;
ans = (num%mod*(l%mod))%mod;
l--;
LL tmp = 1;
while(1){
LL t = l/tmp;
if(t & 1)
t = t%mod*(((t+1)/2)%mod)%mod;
else
t = (t/2)%mod*((t+1)%mod)%mod;
ans = (ans+(t*(tmp%mod)%mod))%mod;
tmp <<= 1;
if(tmp > l)
break;
}
return (ans+1)%mod;
}
int main(void)
{
a[1] =a[2]= 1;
for(int i = 3;i < maxn; ++i)
a[i] = (a[i-a[i-1]]+a[i-1-a[i-2]])%mod;
for(int i = 1;i < maxn;++i)
a[i] = (a[i] +a[i-1])%mod;
int T;
scanf("%d",&T);
for(int i = 1;i <= T; ++i){
scanf("%lld",&n);
LL ans = F(n);
printf("%lld\n",ans);
}
return 0;
}




 京公网安备 11010502036488号
京公网安备 11010502036488号