题目链接:
https://www.lydsy.com/JudgeOnline/problem.php?id=4888
思路:
先求个前缀和,区间的和就是sum[r]-sum[l-1],固定枚举r,如果能够有办法快速知道有多少个sum[l-1]满足sum[r]-sum[l-1]的第k位是1的话,那就能够解决了,如果统计出来是奇数个,那最后答案的第k位就是1
怎么快速知道有多少个sum[l-1]满足sum[r]-sum[l-1]的第k位是1
(一)分类讨论
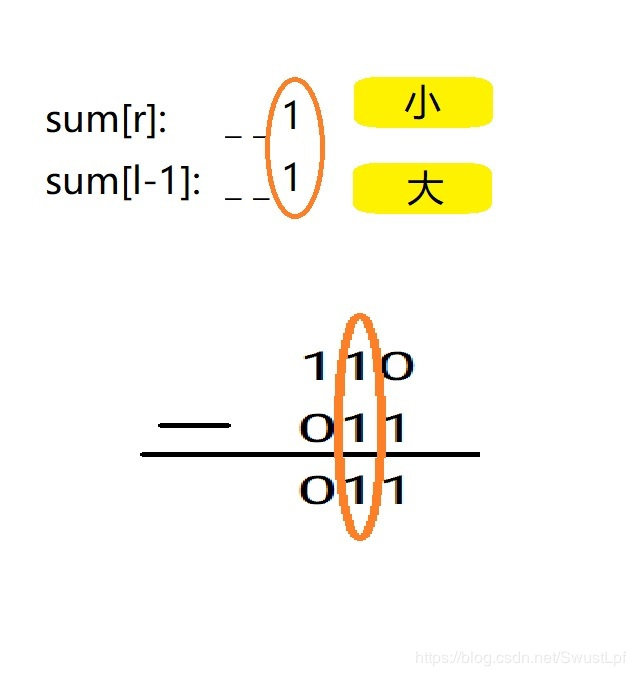
①:sum[r]和sum[l-1]的第k位都是1的时候
就比如图上这个,6的第2位是1,3的第2位是1,但减了之后的结果还是1,至于为什么自己算算就知道了
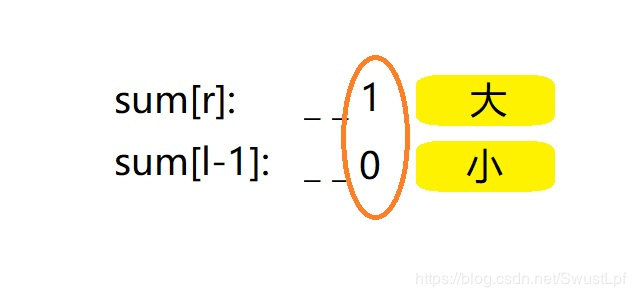
②:sum[r]的第k位是1,sum[l-1]的第k位是0
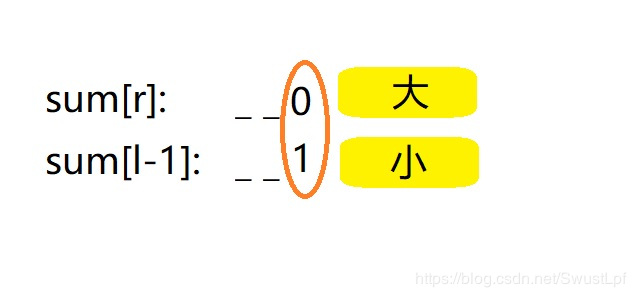
③:sum[r]的第k位是0,sum[l-1]的第k位是1
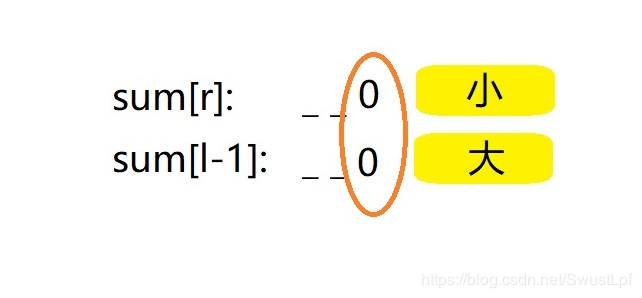
④:都是0的情况
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
const int MOD=1e9+7;
int tree[2][maxn];
int sum[maxn],P[maxn];
int N;
void Add(int pos,int v,int cmd)
{
if(pos<1)return ;
for(int i=pos; i<=N; i+=i&-i)tree[cmd][i]+=v;
}
int getsum(int pos,int cmd)
{
int res=0;
for(int i=pos; i>0; i-=i&-i)res+=tree[cmd][i];
return res;
}
int solve()
{
int res=0;
for(int k=0; k<=20; k++)
{
int cnt[2]={0};//记录第k为是1和是0的个数
int tp=0;
memset(tree,0,sizeof tree);
for(int i=1; i<=N; i++)P[i]=sum[i]%(1<<(k));//0也要算进去
sort(P+1,P+1+N);
int n=unique(P+1,P+1+N)-(P+1);
for(int i=1; i<=N; i++)
{
int now=sum[i];
int pos=lower_bound(P+1,P+1+n,now%(1<<k))-P;
int cmd=(now>>k)&1;
int mi0=getsum(pos,0);//第k位是0,且小于等于now%(1<<(k))的个数
int mi1=getsum(pos,1);//第k位是1,且小于等于now%(1<<(k))的个数
int mx0=cnt[0]-getsum(pos,0);//第k位是0,且大于now%(1<<(k))的个数
int mx1=cnt[1]-getsum(pos,1);//第k位是1,且大于now%(1<<(k))的个数
if(cmd)tp+=mx1+mi0;
else tp+=mi1+mx0;
if(cmd)tp++;//sum[i]-sum[0]这段
cnt[cmd]++;
Add(pos,1,cmd);
}
if(tp&1)res|=(1<<k);
}
return res;
}
int main()
{
while(cin>>N)
{
for(int i=1; i<=N; i++)
{
scanf("%d",sum+i);
sum[i]+=sum[i-1];
}
cout<<solve()<<endl;
}
}
(二)用不等式
第k位是1,是不是就相当于 (sum[r]−sum[l−1])%2k+1≥2k
相当于要找满足 (sum[r]−X)%2k+1≥2k的 X%2k+1的数量
所以先拆开来看:
sum[r]%2k+1−X%2k+1≥2k
①:正常的那种
比如 (11−5)%4≥2
拆开后:
11%4−5%4≥2
变成
3−1≥2
就还是成立
所以这种直接就是变形成:
X%2k+1≤sum[r]%2k+1−2k
②:不正常的那种
比如 (12−5)%4≥2
拆开后:
12%4−5%4≥2
变成
0−1≥2
就不成立了
所以此时左边就还要加上 2k+1才成立
所以这种情况就是
sum[r]%2k+1−X%2k+1+2k+1>=2k
变哈形就是:
X%2k+1≤sum[r]%2k+1+2k
而这种不正常的情况的条件就是 X%2k+1≥sum[r]%2k+1
所以这种情况的 X就是夹在中间的:
sum[r]%2k+1≤X%2k+1≤sum[r]%2k+1+2k
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
const int MOD=1e9+7;
int tree[maxn];
int sum[maxn],P[maxn];
int N,n;
void Add(int pos)
{
pos++;//因为有0这个位置,所以树状数组的都加1
if(pos<1)return ;
for(int i=pos; i<maxn; i+=i&-i)tree[i]++;;
}
int getsum(int pos)
{
pos++;
int res=0;
for(int i=pos; i>0; i-=i&-i)res+=tree[i];
return res;
}
int idx(int x)//找最后一个小于等于他的数,所以是upper_bound-1
{
return upper_bound(P,P+n+1,x)-P-1;//注意,还有减1
}
int solve()
{
int res=0;
for(int k=0; k<=19; k++)
{
memset(tree,0,sizeof tree);
int tp=0;
for(int i=1;i<=N;i++)P[i]=sum[i]%(1<<(1+k));
sort(P,P+1+N);
//unique这里弄出来是有n+1个数,但是我想把P[n]作为最后一个数,因此,还减了一个1
n=unique(P,P+1+N)-P-1;
for(int i=0;i<=N;i++)//这里要从0开始,我也不是很懂为什么
{
int now=sum[i]%(1<<(k+1));
Add(idx(now));
tp+=getsum(idx(now-(1<<k)));//第一个不等式
tp+=getsum(idx(now+(1<<k)))-getsum(idx(now));//第二个不等式,求夹在中间的那一坨
}
if(tp&1)res|=(1<<k);
}
return res;
}
int main()
{
while(cin>>N)
{
for(int i=1; i<=N; i++)
{
scanf("%d",sum+i);
sum[i]+=sum[i-1];
}
cout<<solve()<<endl;
}
}
/* input 3 2 9 9 output 15 */




 京公网安备 11010502036488号
京公网安备 11010502036488号