描述
题目描述
首先给定了我们一个长度为的绳子, 然后我们需要把这个绳子分成段, 然后我们问我们这个段的最大的乘积是多少
题解
解法一: 我们暴力思考, 进行一个数学推导
实现思路
我们可以对这个考虑一下数学思想的一个证明

根据算数几何均值不等式可以知道以下结论
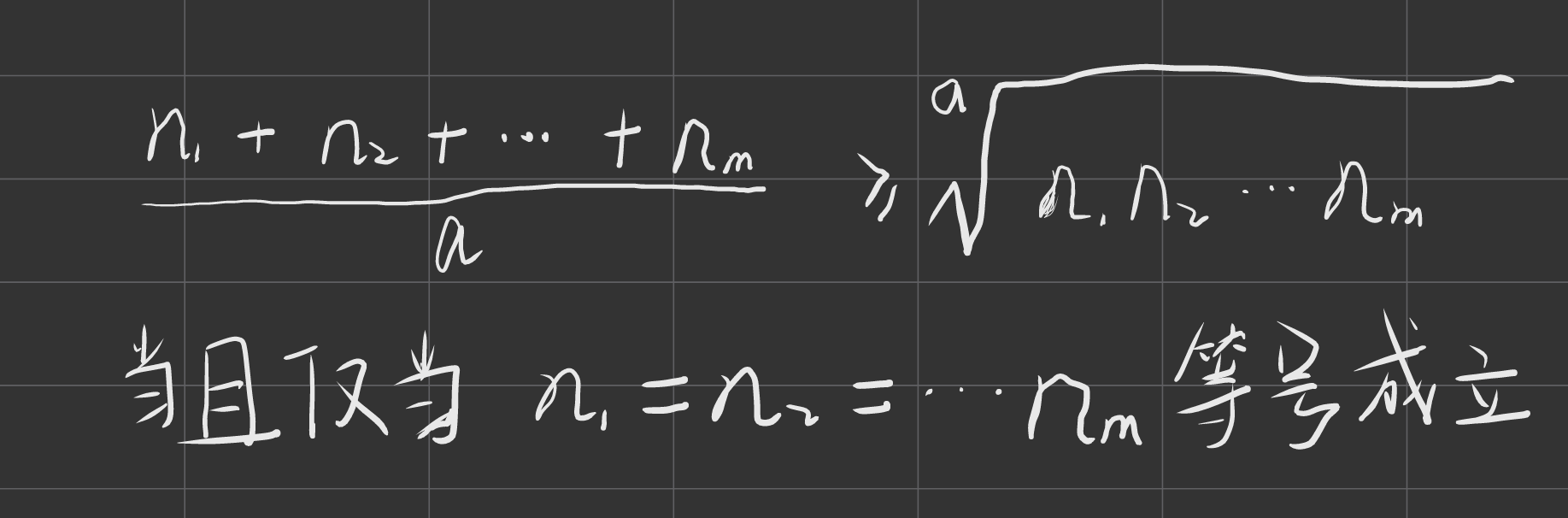
得到推论: 将绳子以相等的长度分为多段得到的乘积最大
我们将绳子按照长度等分成为段, , 然后我们的乘积就是, 然后我们可以得到这样的一个式子

我们其实就是对于最后的式子求极大值, 这个根据求导可得, 这里不过于赘述, 最后我们可以知道驻点是
然后我们的切分长度要求是为整数, 我们考虑和哪一个更是接近我们的
我们可以把这个和分别带入我们上述的, 我们可以发现我们的的值更大, 所以我们每次最好的方式就是每次都尽可能的切成长度为的
那么我们的算法流程就是可以确定了下来
- 如果我们按照长度为进行一个切分, 如果最后剩下的是, 不用考虑了
- 如果最后留下来的是, 我们不拆分
- 如果最后留下来的是, 我们把之前的一个变成
代码实现
class Solution {
const int mod = 998244353;
public:
long long cutRope(long long number) {
if (number <= 3) return number - 1;
// 如果不到3我们可以直接计算
long long cnt = 0;
while (number > 4) {
cnt += 1;
number -= 3;
}
// 计算我们的这个有多少段3
long long res = 1;
for (int i = 1; i <= cnt; i++) res = (res % mod * 3 % mod) % mod;
// 得到我们最后的答案
return res * number % mod;
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们需要运算次, 是级别的
空间复杂度:
理由如下: 我们只引入了常数级别的空间
解法二: 快速幂
实现思路:
首先我们要考虑这么一个问题, 这个数据范围如果我们正常的的做法肯定是会, 那么我们就是需要考虑一种算法这种的时间复杂度要可以达到或者是, 那么我们再去考虑我们上面慢在哪里, 我们是不是慢在一次次的寻找上面, 那么我们其实可以发现我们最简单的一个问题, 如果优化这个方面, 我们可以得到以下的算法思路
- 如果我们可以整除, 那么我们可以直接计算
- 如果我们除余, 那么我们结果就是
- 如果我们余, 我们结果就是
代码实现
class Solution {
const long long mod = 998244353;
public:
long long qpow(long long a, long long b) {
long long res = 1 % mod;
a %= mod;
while (b) {
if (b & 1) res = res * a % mod;
// 如果我们这位的二进制有值, 那么我们可以把这位乘上他的权重
a = a * a % mod;
// 更新权重
b >>= 1;
// 调整我们的b
}
return res;
}
// 快速幂
long long cutRope(long long number) {
if (number <= 3) return number - 1;
// 如果不到3我们可以直接计算
if (number % 3 == 0) return qpow(3, number / 3) % mod;
// 如果正好整除
else if (number % 3 == 1) return qpow(3, number / 3 - 1) * 4 % mod;
// 如果最后余1
else return qpow(3, number / 3) * 2 % mod;
// 如果余是2
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们的快速幂本质就是我们对我们的二进制位和它们的权值进行一个计算, 那么我们也就是需要遍历我们的所有的二进制位, 然后我们一个数的二进制位数也就是级别的
空间复杂度:
理由如下: 我们未引用额外的空间






 京公网安备 11010502036488号
京公网安备 11010502036488号