题目背景

SHOI2012 D2T1

题目描述

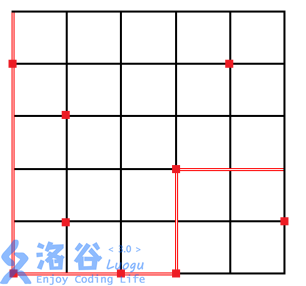
\(2046\) 年 \(OI\) 城的城市轨道交通建设终于全部竣工，由于前期规划周密，建成后的轨道交通网络由\(2n\)条地铁线路构成，组成了一个\(n\)纵\(n\)横的交通网。如下图所示，这\(2n\)条线路每条线路都包含\(n\)个车站，而每个车站都在一组纵横线路的交汇处。

出于建设成本的考虑，并非每个车站都能够进行站内换乘，能够进行站内换乘的地铁站共有\(m\)个，在下图中，标上方块标记的车站为换乘车站。已知地铁运行 \(1\) 站需要 \(2\) 分钟，而站内换乘需要步行 \(1\) 分钟。\(Serenade\) 想要知道，在不中途出站的前提下，他从学校回家最快需要多少时间（等车时间忽略不计）。

输入输出格式

输入格式：

第一行有两个整数\(n,m\)。

接下去\(m\)行每行两个整数\(x,y\),表示第\(x\)条横向线路与第\(y\)条纵向线路的交

汇站是站内换乘站。

接下去一行是四个整数\(x_1,y_1,x_2,y_2\)。表示 \(Serenade\) 从学校回家时，在第 \(x_1\)条横向线路与第\(y_1\)​条纵向线路的交汇站上车，在第\(x_2\)​条横向线路与第\(y_2\)​条纵向线路的交汇站下车。

输出格式：

输出文件只有一行，即 \(Serenade\) 在合理选择线路的情况下，回家所需要的时间。如果 \(Serenade\) 无法在不出站换乘的情况下回家，请输出\(-1\)。

输入输出样例

输入样例#1：

2 1
1 2
1 1 2 2

输出样例#1：

5

输入样例#2：

6 9
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
1 1 4 6

输出样例#2：

27

输入样例#3：

6 10
2 1
2 5
3 2
4 4
5 2
5 6
6 1
6 3
6 4
6 6
1 1 4 6

输出样例#3：

26

说明

对于 \(30\%\)的数据，\(n\le 50,m\le 1000\)；

对于 \(60\%\)的数据，\(n\le 500,m\le 2000\)；

对于 \(100\%\)的数据，\(n\le 20000,m\le 100000\)；

思路：
裸的分层最短路，对于这个题目来说，层与层之间的权值为\(1\)。

而且看数据范围，\(n\)这么大的一个范围，肯定不能\(n^2\)存图了，那么我们就枚举每个中转点(换乘点)，横纵分别求两个中转点之间的距离，然后存下来，每层起点和起点的映射及终点和终点的映射都要是0，然后直接上堆优化dijkstra，这个题就做完了。

分层最短路需要注意的问题:

1、数组的大小，这个很重要。

2、确定每层之间的权值是多少。

3、考虑如何建边。

注意了这三个问题之后，分层最短路就跟裸的最短路没什么区别了……

于是我们开开心心的来看代码(代码就不解释了，有了思路就能看懂)：

#include<cstdio>
#include<algorithm>
#include<queue>
#include<cctype>
#include<cstring>
#define maxn 200001
using namespace std;
int num,n,m,head[800001],dis[800001];
inline int qread() {
  char c=getchar();int num=0,f=1; 
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';return num*f;
} 
struct edge {
  int v,w,nxt;
}e[800001];
struct node {
  int x,y;
  bool operator < (const node &a) const {return y>a.y;}
};
struct Edge {
  int x,y,id;
}zrj[maxn];
bool cmp1(Edge a,Edge b){if(a.x==b.x)return a.y<b.y;return a.x<b.x;}
bool cmp2(Edge a,Edge b){if(a.y==b.y)return a.x<b.x;return a.y<b.y;}
inline void ct(int u, int v, int w) {
  e[++num].v=v;
  e[num].w=w;
  e[num].nxt=head[u];
  head[u]=num;
}
priority_queue<node>q;
inline void dijkstra() {
  memset(dis,0x3f,sizeof(dis)); 
  dis[m+1]=0;q.push((node){m+1,0});
  while(!q.empty()) {
    int u=q.top().x,d=q.top().y;
    q.pop();
    if(d!=dis[u]) continue;
    for(int i=head[u];i;i=e[i].nxt) {
      int v=e[i].v;
      if(dis[v]>dis[u]+e[i].w) {
        dis[v]=dis[u]+e[i].w;
        q.push((node){v,dis[v]});
      } 
    }
  }
}
int main() {
  n=qread(),m=qread();
  for(int i=1;i<=m+2;++i) zrj[i].x=qread(),zrj[i].y=qread(),zrj[i].id=i;
  sort(zrj+1,zrj+m+3,cmp1);
  for(int i=1;i<m+2;++i)
  {if(zrj[i].x==zrj[i+1].x) ct(zrj[i].id,zrj[i+1].id,(zrj[i+1].y-zrj[i].y)*2),ct(zrj[i+1].id,zrj[i].id,(zrj[i+1].y-zrj[i].y)*2);}
  sort(zrj+1,zrj+m+3,cmp2);
  for(int i=1;i<m+2;++i) 
  {if(zrj[i].y==zrj[i+1].y) ct(zrj[i].id+m+2,zrj[i+1].id+m+2,(zrj[i+1].x-zrj[i].x)*2),ct(zrj[i+1].id+m+2,zrj[i].id+m+2,(zrj[i+1].x-zrj[i].x)*2);}
  for(int i=1;i<=m;++i) ct(i,i+m+2,1),ct(i+m+2,i,1); 
  ct(m+1,m*2+3,0),ct(m*2+3,m+1,0);ct(m+2,m*2+4,0),ct(m*2+4,m+2,0);
  dijkstra();
  if(dis[m+2]>1e9) printf("-1\n");
  else printf("%d\n",dis[m+2]);
  return 0;
}

希望这篇题解可以对大家了解分层最短路有些帮助。