基础数据结构——1.3栈
HDU1062 Text Reverse
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Problem Description
Ignatius likes to write words in reverse way. Given a single line of text which is written by Ignatius, you should reverse all the words and then output them.
Input
The input contains several test cases. The first line of the input is a single integer which is the number of test cases. test cases follow. Each test case contains a single line with several words. There will be at most characters in a line.
Output
For each test case, you should output the text which is processed.
Sample Input
3 olleh !dlrow m'I morf .udh I ekil .mcaSample Output
hello world! I'm from hdu. I like acm.Hint
Remember to use
getchar()to read'\n'after the integer , then you may usegets()to read a line and process it.Author
Ignatius.L
题目大意
输入 行单词,将所有单词翻转后输出.
栈有栈顶 ,栈内元素是讲究顺序的,元素只能放入栈顶或从栈顶取出.
栈如图1.3.1.所示,其中 代表栈内的元素.
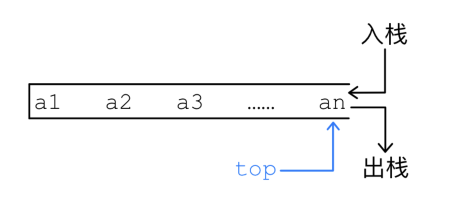
1.3.1 STL stack
STL stack 的部分基本操作1
C++ STL中有封装好的栈(stack)容器,引用 stack 头文件即可使用,其有如下几种基本操作:
stack<T> s:定义存储元素的数据类型为T的队列变量,其变量名为s.s.top():返回栈s栈顶的元素.s.push(x):将x放入栈s的栈顶.s.pop():将栈s的栈顶元素删除.s.size():返回栈s内的元素个数.s.empty():检查栈s是否为空,若栈s中没有元素则返回true,否则返回false.
使用
s.top()、s.pop()这类直接调用栈内元素的函数时,要注意先判断栈是否为空.如果栈为空就使用这些函数会导致程序运行时错误(Runtime Error).
STL stack 的部分基本操作如图1.3.2所示.
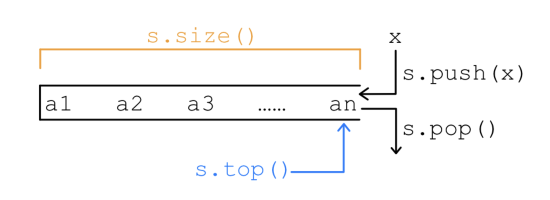
STL stack 和 STL queue 一样,不能随机访问栈内的元素.
即试图用
s[2]来获得栈s中的第二个元素是不可行的.
代码实现
对于单个单词,可以先将其全部字符入栈,之后再将字符逐个从栈顶取出,就可以实现单词的翻转.
如图1.3.3为单词 olleh 依靠栈进行翻转的示例.
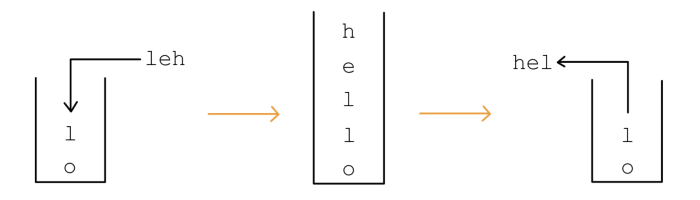
//HDU1062TextReverse-STLstack写法
#include<bits/stdc++.h>
using namespace std;
void solve() {
string s; getline(cin, s); s += ' ';
int len = s.size();
stack<char>st;
for (int i = 0; i < len; ++i) {
if (s[i] == ' ') {
while (!st.empty()) {
cout << st.top();
st.pop();
}
cout << " \n"[i == len - 1];
} else st.push(s[i]);
}
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T; cin >> T; cin.ignore();
while (T--) solve();
return 0;
}
这份代码有很多需要说明的地方:
ios::sync_with_stdio(0); cin.tie(0);这两句的效果是关闭cin/cout的流同步,这样
cin/cout就可以和scanf/printf一样快,但此时cin/cout就不能与scanf/printf/getchar/putchar/gets/puts混用.每行单词的数量是不定的,只会在输入数据的第一行给出一个 代表接下来字符串的行数,
不论是用
scanf(“%s”,s)来读取字符数组(char [])s,还是用cin>>s读取字符串(string)s,都没办法读取空格,它们都会在读到空格时结束,这里使用
getline(cin,s)来读取整行的字符串(string)s,当然也可以用gets(s)来读取整行的字符数组(char [])s,但由于关闭了流同步,故这里是用
getline.第一行不止有一个整数 ,还会有一个回车(其实数据除了最后一行外,每行末尾都会有回车,只是
scanf/cin不去读取它罢了),如果在读取 之后立刻使用
getline,则还没有被读取的回车就会被读到,从而影响数据的读入,这里使用
cin.ignore()来忽略行末回车,这样再使用getline就会从下一行开始读入.C++ STL中封装好的字符串(string)容器可以看作不定长的字符数组,引用
string头文件即可使用,这里先介绍一下 STL string 的部分基本操作:
string s:定义一个字符串s,如没有赋值则字符串s默认为空.
s[i]:返回字符串s下标为 的字符(从 开始计数).
s.size():返回字符串s的长度.
s+=ch:在字符串s的末尾接上一个字符或字符串ch.使用
s[i]这类调用字符串的字符的函数(或功能)时,要注意先判断字符串的长度是否允许其有这样一个字符.对于当前行,可以以空格为分隔,遍历字符串
s时,遇到空格就代表当前单词的结束,将栈st内的字符全部出栈.特别地,最后一个单词后面没有空格,则可以人为在字符串
s末尾添加一个空格.注意除了单词外空格也要被输出,但人为添加的空格不应该被输出,
如果字符串
s遍历到了最后一个字符,它一定是人为添加的那个空格,就可以输出一个回车而不是空格,这里使用的是
cout<<" \n"[i==len-1];,是将" \n"当做没有名字的字符数组/字符串,其第一个字符是
" \n"[0]空格,第二个字符是" \n"[1]回车,
len代表字符串s的长度,当i==len-1为真时,字符串s遍历到了最后一个字符,则输出字符" \n"[1],否则就需要输出字符" \n"[0].
时间复杂度分析
设数据中字符串的长度为 ,则总的时间复杂度为 .
1.3.2 手写栈
可以使用结构体或数组来实现栈,这里用数组 模拟栈,用 表示栈顶在数组 内的下标,有:
- 当栈为空时,有 .
- 栈内元素个数为 (因为栈的元素从 开始存起).
- 栈顶元素为 .
- 删除栈顶只需要 ,不需要对 进行修改,因为之后如果有元素入栈会覆盖掉它的值.
如下为使用数组实现栈的参考代码.
//HDU1062TextReverse-手写栈写法
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
char st[N];
int top;
void solve() {
string s; getline(cin, s); s += ' ';
int len = s.size();
top = -1;
for (int i = 0; i < len; ++i) {
if (s[i] == ' ') {
while (top != -1) {
cout << st[top];
--top;
}
cout << " \n"[i == len - 1];
} else st[++top] = s[i];
}
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T; cin >> T; cin.ignore();
while (T--) solve();
return 0;
}
时间复杂度分析
本代码时间复杂度与 STL stack 几乎没有区别,为 .
1.3.3 单调栈
洛谷 P2947 [USACO09MAR]Look Up S
时间限制:1.00s 内存限制:125.00MB题目描述
约翰的 头奶牛站成一排,奶牛 的身高是 。现在,每只奶牛都在向右看齐。对于奶牛 ,如果奶牛 满足 且 ,我们可以说奶牛 可以仰望奶牛 。 求出每只奶牛离她最近的仰望对象。
输入格式
第 行输入 ,之后每行输入一个身高 。
输出格式
共 行,按顺序每行输出一只奶牛的最近仰望对象,如果没有仰望对象,输出 。
样例输入
6 3 2 6 1 1 2样例输出
3 3 0 6 6 0提示
【输入说明】 头奶牛的身高分别为 3,2,6,1,1,2。
【输出说明】奶牛 1,2 仰望奶牛 3,奶牛 4,5 仰望奶牛 6,奶牛 3 和 6 没有仰望对象。
【数据规模】
对于 的数据:;
对于 的数据:;
对于 的数据:。
单调栈是指栈内的元素按照入栈顺序、以某种规则呈现出(非)递增/递减的特点的栈.
在本题中,考虑当前遍历到了第 只奶牛,则:
- 若栈顶奶牛的身高 ,则栈顶的奶牛出栈,并且可以说栈顶奶牛最近的仰望对象是第 只奶牛,直到栈为空或栈顶奶牛的身高 ,将第 只奶牛入栈.
- 注意,若栈顶奶牛和第 只奶牛身高相同,栈顶奶牛是不仰望第 只奶牛的.
这样可以保证:
- 栈内的元素从栈顶开始是非递减的,如果入栈早的奶牛比入栈晚的奶牛矮,则入栈早的奶牛会被入栈晚的奶牛挤出栈.
- 当遍历到第 只奶牛时,若在第 只奶牛入栈后,栈内的一部分元素为 ( 更靠近栈顶),则其保证了 是 范围内的最高的奶牛.
- 因为栈内的元素从栈顶开始是非递减的,有 .
- 若 前面没有 存在,则 是 范围内最高的奶牛.
代码实现
在代码实现时,为了方便知道栈顶奶牛是第几只奶牛,这里并不在单调栈中直接存奶牛的身高,而是存储它是第几只奶牛.
如下为使用 STL stack 的参考代码.
//洛谷P2947LookUpS-单调栈写法
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int h[N], ans[N];
int main() {
int n; scanf("%d", &n);
stack<int>s;
for (int i = 1; i <= n; ++i) {
scanf("%d", &h[i]);
while (!s.empty() && h[s.top()] < h[i]) {
ans[s.top()] = i;
s.pop();
}
s.push(i);
}
for (int i = 1; i <= n; ++i) printf("%d\n", ans[i]);
return 0;
}
时间复杂度分析
这份代码看似有
while循环,但是出栈的元素不会再次入栈.总共会有 个元素入栈,再考虑总共有 只奶牛,总的时间复杂度为 .
习题
洛谷 P1739 表达式括号匹配
时间限制:1.00s 内存限制:128.00MB题目描述
假设一个表达式有英文字母(小写)、运算符(
+、-、*、/)和左右小(圆)括号构成,以@作为表达式的结束符。请编写一个程序检查表达式中的左右圆括号是否匹配,若匹配,则输出YES;否则输出NO。表达式长度小于 ,左圆括号少于 个。输入格式
一行:表达式。
输出格式
一行:
YES或NO。样例 #1
样例输入
2*(x+y)/(1-x)@样例输出
YES样例 #2
样例输入
(25+x)*(a*(a+b+b)@样例输出
NO提示
表达式长度小于 ,左圆括号少于 个。
题解
从头到尾遍历字符串(表达式),设当前遍历到的字符为 ,则:
- 若 不是左括号/右括号,则忽略它.
- 若
(,则将其入栈. - 若
),则检查栈内是否有(,若有则认为一对括号()匹配上了,否则(即栈空)则认为匹配失败.
遍历完之后,检查栈内是否还有剩余没有匹配成功的 (,若有则认为匹配失败,没有则匹配成功.
代码实现
如下为使用 STL stack 的参考代码.
//洛谷P1739表达式括号匹配-STLstack写法
#include<bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(0); cin.tie(0);
string s; cin >> s;
stack<char>st;
for (auto ch : s) {
if (ch == '(') st.push(ch);
if (ch == ')') {
if (st.empty()) { cout << "NO"; return 0; }
st.pop();
}
}
if (!st.empty()) cout << "NO";
else cout << "YES";
return 0;
}
这份代码的第 行使用了 C++11 标准开始支持的
for循环遍历方法.
auto可以自动判断ch的数据类型,ch则是遍历过程中的s这一容器内的元素,这里的for (auto ch : s)作用相当于
for (int i = 0; i < s.size(); ++i) { char ch = s[i]; }
时间复杂度分析
设字符串的长度为 ,本代码时间复杂度为 .
洛谷 P1449 后缀表达式
时间限制:1.00s 内存限制:125.00MB题目描述
所谓后缀表达式是指这样的一个表达式:式中不再引用括号,运算符号放在两个运算对象之后,所有计算按运算符号出现的顺序,严格地由左而右新进行(不用考虑运算符的优先级)。
如: 对应的后缀表达式为:。在该式中,
@为表达式的结束符号。.为操作数的结束符号。输入格式
输入一行一个字符串 ,表示后缀表达式。
输出格式
输出一个整数,表示表达式的值。
样例输入
3.5.2.-*7.+@样例输出
16提示
数据保证,,答案和计算过程中的每一个值的绝对值不超过 。
题解
遇到运算符号时,需要从栈顶连续取出两个数字,对这两个数字按照运算符号进行计算。这里会有一个问题:
-
设从栈顶取出的第一个数为 ,从栈顶取出的第二个数为 ,若运算符号为
-或/,则得到的结果应该是 或 .例如样例中的
3.5.2.-这一部分,当遇到-时从栈顶取出的第一个数为2,从栈顶取出的第二个数为5,而计算的应该是5-2.
代码实现
在读入数字时,由于一开始直接读入整个字符串,所以让数字入栈时,需要对两位及以上的数字进行处理.
可以发现 .
若现在需要读入的这个数字是 ,则对于字符串遍历到的当前字符 ,有:
- 若
'0''9',则有'0'. - 若
'.',则说明这个数字读入完成,将 的值入栈,随后将 清空.
如下为使用 STL stack 的参考代码.
//洛谷P1449后缀表达式-STLstack写法
#include<bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(0); cin.tie(0);
string s; cin >> s;
int n = s.size();
int num = 0;
stack<int>st;
for (int i = 0; i < n; ++i)
if (s[i] == '@')
break;
else if (s[i] == '.') {
st.push(num);
num = 0;
} else if ('0' <= s[i] && s[i] <= '9')
num = num * 10 + s[i] - '0';
else {
int a = st.top(); st.pop();
int b = st.top(); st.pop();
if (s[i] == '+') st.push(b + a);
if (s[i] == '-') st.push(b - a);
if (s[i] == '*') st.push(b * a);
if (s[i] == '/') st.push(b / a);
}
cout << st.top();
return 0;
}
时间复杂度分析
时间复杂度为 .
洛谷 P1981 [NOIP2013 普及组] 表达式求值
时间限制:1.00s 内存限制:125.00MB题目描述
给定一个只包含加法和乘法的算术表达式,请你编程计算表达式的值。
输入格式
一行,为需要你计算的表达式,表达式中只包含数字、加法运算符 “” 和乘法运算符 “”,且没有括号,所有参与运算的数字均为 到 之间的整数。
输入数据保证这一行只有 、、 这 种字符。
输出格式
一个整数,表示这个表达式的值。
注意:当答案长度多于 位时,请只输出最后 位,前导 不输出。
样例 #1
样例输入
1+1*3+4样例输出
8样例 #2
样例输入
1+1234567890*1样例输出
7891样例 #3
样例输入
1+1000000003*1样例输出
4提示
对于 的数据, 表达式中加法运算符和乘法运算符的总数 。
对于 的数据, 表达式中加法运算符和乘法运算符的总数 。
对于 的数据, 表达式中加法运算符和乘法运算符的总数 。
题解
对于多位数字的处理已经在洛谷 P1449 后缀表达式一题中解决了,现在需要解决如何计算表达式.
定义一个数字栈 和一个符号栈 ,考虑从头到尾遍历表达式,则:
-
若遇到数字就将其放入数字栈 .
-
若遇到
+,则检查符号栈 的栈顶符号是否为*.-
如果符号栈 栈顶符号是
*就从数字栈 内取出两个数字进行乘法运算后再放回数字栈 ,并将*从符号栈 中取出.直到符号栈 为空或栈顶符号不是
*. -
如果符号栈 栈顶符号是
+则正常将新遍历到的+放入符号栈 .
-
-
若遇到
*,则将其放入符号栈 即可.
本题的关键是处理
+和*的运算优先级导致的运算顺序的改变.如果新进来一个
+,那么在+之前的*的运算优先级会更高,需要先计算*得到的结果才能让+的计算进行.
遍历完后,只要符号栈 不为空,就从数字栈 中取出两个数字按照符号栈 栈顶符号进行计算.
将计算结果再放回数字栈 的栈顶,并将符号栈 的栈顶符号删除.
最后只有数字栈内剩余一个数字,即为表达式的计算结果.
代码实现
不要忘记表达式遍历结束时,会有一个数字,要注意将其放入数字栈 .
//P1981[NOIP2013 普及组]表达式求值-STLstack写法
#include<bits/stdc++.h>
using namespace std;
string s;
stack<int>num;
stack<char>opt;
void calc() {
int a = num.top(); num.pop();
int b = num.top(); num.pop();
if (opt.top() == '+') num.push((b + a) % 10000);
if (opt.top() == '*') num.push((b * a) % 10000);
opt.pop();
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> s;
int x = 0;
for (auto ch : s) {
if ('0' <= ch && ch <= '9') x = (x * 10 + ch - '0') % 10000;
else {
num.push(x); x = 0;
while (ch == '+' && !opt.empty() && opt.top() == '*') calc();
opt.push(ch);
}
}
num.push(x);
while (!opt.empty()) calc();
cout << num.top();
return 0;
}
时间复杂度分析
设表达式的长度为 ,本代码时间复杂度为 .
洛谷 P1175 表达式的转换
时间限制:1.00s 内存限制:128.00MB题目描述
平常我们书写的表达式称为中缀表达式,因为它将运算符放在两个操作数中间,许多情况下为了确定运算顺序,括号是不可少的,而后缀表达式就不必用括号了。
后缀标记法:书写表达式时采用运算紧跟在两个操作数之后,从而实现了无括号处理和优先级处理,使计算机的处理规则简化为:从左到右顺序完成计算,并用结果取而代之。
例如:
8-(3+2*6)/5+4可以写为:8 3 2 6 * + 5 / - 4 +其计算步骤为:
8 3 2 6 * + 5 / - 4 + 8 3 12 + 5 / - 4 + 8 15 5 / - 4 + 8 3 - 4 + 5 4 + 9编写一个程序,完成这个转换,要求输出的每一个数据间都留一个空格。
输入格式
就一行,是一个中缀表达式。输入的符号中只有这些基本符号
0123456789+-*/^(),并且不会出现形如2*-3的格式。表达式中的基本数字也都是一位的,不会出现形如
12形式的数字。所输入的字符串不要判错。
输出格式
若干个后缀表达式,第 行比第 行少一个运算符和一个操作数,最后一行只有一个数字,表示运算结果。
样例 #1
样例输入
8-(3+2*6)/5+4样例输出
8 3 2 6 * + 5 / - 4 + 8 3 12 + 5 / - 4 + 8 15 5 / - 4 + 8 3 - 4 + 5 4 + 9样例 #2
样例输入
2^2^3样例输出
2 2 3 ^ ^ 2 8 ^ 256提示
运算的结果可能为负数,
/以整除运算。并且中间每一步都不会超过 。字符串长度不超过 。注意乘方运算
^是从右向左结合的,即2 ^ 2 ^ 3为2 ^ (2 ^ 3),后缀表达式为2 2 3 ^ ^。其他同优先级的运算是从左向右结合的,即
4 / 2 / 2 * 2为((4 / 2) / 2) * 2,后缀表达式为4 2 / 2 / 2 *。保证不会出现计算乘方时幂次为负数的情况,故保证一切中间结果为整数。
题解
在这里先讨论运算符号的优先级:
(和)虽然不是运算符号,但是这里仍认为它们的运算优先级为 .+和-的运算优先级为 .*和/的运算优先级为 .^的运算优先级为 .
依旧设计一个数字栈 和一个符号栈 从头到尾遍历表达式,有:
-
若遍历到了数字,则将数字放入数字栈 .
-
若遍历到了
(,则直接将其放入符号栈 . -
若遍历到了
),则进行计算,直到符号栈 的栈顶符号为(时停止,并将此(删除.计算指的就是从数字栈 中取出两个数字,按照符号栈 的栈顶运算符号进行计算,计算结果放回数字栈 ,并且将该运算符号从符号栈 中删除.
-
若遍历到了
+-*/,则进行计算,直到符号栈 为空或栈顶的运算符号的优先级小于该运算符号,再将该运算符号放入符号栈 .注意就算优先级相等,仍需要进行计算,例如
3-2+5,就不应该先计算2+5,而是应该先计算3-2. -
特别地,由于
^是从右向左结合,故只需要直接放入符号栈 即可.因为
2^2^3,可以发现其先计算的2^3,再计算的2^(2^3).
遍历完表达式后,进行计算直到符号栈 为空.
这里考虑储存题目要求的答案,每行答案由若干个字符串组成,有:
-
当数字放入数字栈 时,所有答案行都在末尾放入这个数字.
-
当有计算进行时,新增一行答案,此答案行的内容与原先的其他答案行一致,但其需要取消末尾两个数字,并且不和其他答案行一样放入进行计算的运算符.
每有一次运算进行,就会多一个答案行.
上下两个答案行之间的区别就是上一行答案行最左边的运算符没有进行运算,而下一行答案行是进行过该运算符的运算的.
代码实现
如下为使用 STL stack 的参考代码.
//洛谷P1175表达式的转换-STLstack写法
#include<bits/stdc++.h>
using namespace std;
stack<int>num;
stack<char>opt;
map<char, int>Rank;
vector<vector<string>>ans(1);
void init() {
Rank['('] = Rank[')'] = 0;
Rank['+'] = Rank['-'] = 1;
Rank['*'] = Rank['/'] = 2;
Rank['^'] = 3;
}
void calc() {
int a = num.top(); num.pop();
int b = num.top(); num.pop();
if (opt.top() == '+') num.push(b + a);
if (opt.top() == '-') num.push(b - a);
if (opt.top() == '*') num.push(b * a);
if (opt.top() == '/') num.push(b / a);
if (opt.top() == '^') {
int res = 1;
for (int i = 1; i <= a; ++i) res *= b;
num.push(res);
}
ans.push_back(ans.back());
string OPT = ""; OPT += opt.top();
for (int i = 0; i < ans.size() - 1; ++i) ans[i].push_back(OPT);
ans[ans.size() - 1].pop_back();
ans[ans.size() - 1].pop_back();
ans[ans.size() - 1].push_back(to_string(num.top()));
opt.pop();
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
init();
string s; cin >> s;
for (auto ch : s) {
if ('0' <= ch && ch <= '9') {
for (int i = 0; i < ans.size(); ++i)
ans[i].push_back(to_string(ch - '0'));
num.push(ch - '0');
} else if (ch == '(') {
opt.push(ch);
} else if (ch == ')') {
while (opt.top() != '(') calc();
opt.pop();
} else if (ch != '^') {
while (!opt.empty() && Rank[opt.top()] >= Rank[ch]) calc();
opt.push(ch);
} else opt.push(ch);
}
while (!opt.empty()) calc();
for (auto res : ans)
for (int i = 0; i < res.size(); ++i)
cout << res[i] << " \n"[i == res.size() - 1];
return 0;
}
这份代码有很多需要说明的地方:
C++ STL中封装好的映射(map)容器,可以让一个字符映射成一个数字,引用
map头文件即可使用,这里先介绍一下 STL map 的部分基本操作:
map<T1,T2> mp:定义一种映射规则mp,是一种从数据类型T1映射到数据类型T2的映射规则.
mp[s]=t:将数据类型为T1的变量(或常量)s映射为数据类型为T2的变量(或常量)t.
mp[s]:返回s在映射规则mp下的映射,如果这一规则还没有被定义,则会创建对应数据类型T2默认为空的新规则调用
mp[s]的时间复杂度为 ,其中 为映射mp已经建立的规则的数量.在算法竞赛中, 不加底数默认为是以 为底的,即 .
- 但注意若
s为字符串(string)或其他复杂的数据类型(容器),则还会增加一个判断变量(或常量)是否相等的时间.- 即若
s="abc",则mp需要在已经建立的映射规则中,寻找与"abc"相等的字符串(string).- 设字符串(string)长度为 ,则调用
mp[s]的时间复杂度为 .C++ STL中封装好了不定长的数组,即动态数组(vector),引用
vector头文件即可使用,这里介绍一下 STL vector 的部分基本操作:
vector<T> a:定义一个变量名为a的元素数据类型为T的动态数组a,默认为空.
vector<T> a(x,P):若在变量名后增加(x,P),则其初始化的长度为x,且所有元素的初始值为P(P不填默认为空,则其可以写成vector<T> a(x)).
a[i]:返回动态数组a下标为 的元素(从 开始计数).
a.back():返回动态数组a的末尾元素.
a.size():返回动态数组a的大小.
a.push_back(x):将x添加到动态数组a的末尾(这样动态数组a的大小就会 ).
a.pop_back():将动态数组a的末尾元素删除(这样动态数组a的大小就会 ).使用
a[i]、a.back()、a.pop_back()这类调用动态数组的元素的函数(或功能)时,要注意先判断动态数组内是否有这样的元素.函数
to_string(x):返回数字x转换为的字符串(string).函数
init()使用了映射Rank来定义运算符的优先级.由于保证输入的数字只有个位数,所以类似于
2^3的幂次方运算结果都是直接for循环得到的.定义二维动态数组
ans来保存答案,其中:
ans[i]代表第 行答案(从 开始计数).每行答案是一个元素为
string的数组.
ans[i][j]表示第 行答案的第 个字符串,输出时用空格隔开它们.
时间复杂度分析
每出现一个运算符,就会让答案多输出一行,表达式总长为 ,则最坏的时间复杂度为 .
以下题目的解法已经在本节介绍过(或过于相似)
附件
//洛谷P1175表达式的转换-STLstack写法-允许表达式内数字位数大于一(计算过程中出现的数不能超过int)
#include<bits/stdc++.h>
using namespace std;
stack<int>num;
stack<char>opt;
map<char, int>Rank;
vector<vector<string>>ans(1);
void init() {
Rank['('] = Rank[')'] = 0;
Rank['+'] = Rank['-'] = 1;
Rank['*'] = Rank['/'] = 2;
Rank['^'] = 3;
}
int qpow(int a, int b) { // 多位数的幂次方运算再使用 for 循环可能会超时,这里使用快速幂
int res = 1;
for (; b; b >>= 1, a = a * a)
if (b & 1) res = res * a;
return res;
}
void calc() {
int a = num.top(); num.pop();
int b = num.top(); num.pop();
if (opt.top() == '+') num.push(b + a);
if (opt.top() == '-') num.push(b - a);
if (opt.top() == '*') num.push(b * a);
if (opt.top() == '/') num.push(b / a);
if (opt.top() == '^') num.push(qpow(b, a));
ans.push_back(ans.back());
string OPT = ""; OPT += opt.top();
for (int i = 0; i < ans.size() - 1; ++i) ans[i].push_back(OPT);
ans[ans.size() - 1].pop_back();
ans[ans.size() - 1].pop_back();
ans[ans.size() - 1].push_back(to_string(num.top()));
opt.pop();
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
init();
string s; cin >> s;
int x = 0; bool is_num = 0;
/*
因为类似于 (3+0)/2 这种表示的 )/ 运算符号是连在一起的,并且前面的数字还是 0
这样遇到一个运算符号时,需要确定其是否是紧跟在一个数字结尾的
is_num 代表在遍历到当前字符之前是否在输入一个数字
*/
for (auto ch : s) {
if ('0' <= ch && ch <= '9') { x = x * 10 + ch - '0'; is_num = 1; }
else {
if (is_num) {
for (int i = 0; i < ans.size(); ++i)
ans[i].push_back(to_string(x));
num.push(x); x = 0; is_num = 0;
}
if (ch == '(') {
opt.push(ch);
} else if (ch == ')') {
while (opt.top() != '(') calc();
opt.pop();
} else if (ch != '^') {
while (!opt.empty() && Rank[opt.top()] >= Rank[ch]) calc();
opt.push(ch);
} else opt.push(ch);
}
}
if (is_num) {
for (int i = 0; i < ans.size(); ++i)
ans[i].push_back(to_string(x));
num.push(x);
}
while (!opt.empty()) calc();
for (auto res : ans)
for (int i = 0; i < res.size(); ++i)
cout << res[i] << " \n"[i == res.size() - 1];
return 0;
}
//洛谷P1175表达式的转换-STLstack写法-只输出后缀表达式和答案
#include<bits/stdc++.h>
using namespace std;
stack<int>num;
stack<char>opt;
map<char, int>Rank;
vector<string>ans;
void init() {
Rank['('] = Rank[')'] = 0;
Rank['+'] = Rank['-'] = 1;
Rank['*'] = Rank['/'] = 2;
Rank['^'] = 3;
}
int qpow(int a, int b) {
int res = 1;
for (; b; b >>= 1, a = a * a)
if (b & 1) res = res * a;
return res;
}
void calc() {
int a = num.top(); num.pop();
int b = num.top(); num.pop();
if (opt.top() == '+') num.push(b + a);
if (opt.top() == '-') num.push(b - a);
if (opt.top() == '*') num.push(b * a);
if (opt.top() == '/') num.push(b / a);
if (opt.top() == '^') num.push(qpow(b, a));
string OPT = ""; OPT += opt.top();
ans.push_back(OPT);
opt.pop();
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
init();
string s; cin >> s;
int x = 0; bool is_num = 0;
for (auto ch : s) {
if ('0' <= ch && ch <= '9') { x = x * 10 + ch - '0'; is_num = 1; }
else {
if (is_num) {
ans.push_back(to_string(x));
num.push(x); x = 0; is_num = 0;
}
if (ch == '(') {
opt.push(ch);
} else if (ch == ')') {
while (opt.top() != '(') calc();
opt.pop();
} else if (ch != '^') {
while (!opt.empty() && Rank[opt.top()] >= Rank[ch]) calc();
opt.push(ch);
} else opt.push(ch);
}
}
if (is_num) {
ans.push_back(to_string(x));
num.push(x);
}
while (!opt.empty()) calc();
for (int i = 0; i < ans.size(); ++i)
cout << ans[i] << " \n"[i == ans.size() - 1];
cout << num.top();
return 0;
}




 京公网安备 11010502036488号
京公网安备 11010502036488号