题目大意
给定一个柱状图，求它能包含的最大的矩形的面积。如下图中阴影部分就是要求的矩形。
输入: [2,1,5,6,2,3]
输出: 10
解题思路
栈，难题。
看了半天两个解法，只有下图最容易理解：
http://www.cnblogs.com/zuoyuan/p/3783993.html
https://shenjie1993.gitbooks.io/leetcode-python/084%20Largest%20Rectangle%20in%20Histogram.html
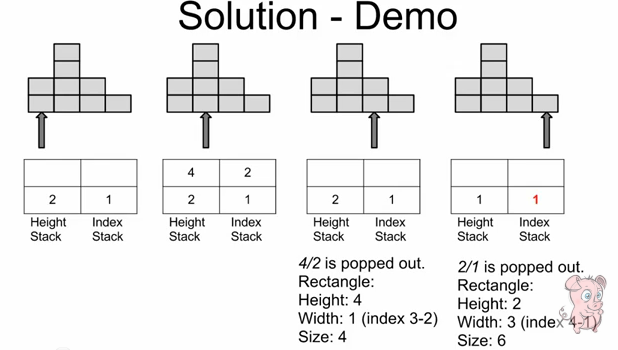
依次遍历柱状结构，如果是递增的则压栈，
如果不是则把比它高的柱依次弹出（只弹出比当前柱高的可以保证把当前柱压栈后，栈中的柱依旧是依次递增的）并计算以该柱为高的矩形的面积。
计算面积时，宽度应该是栈顶元素到遍历到元素之间的宽
如当弹出第二个2（2后面没有比它小的元素，为了使该元素能顺利弹出，在原柱状图末尾加一个0）时，栈顶元素是1，这样就能方便计算出宽度为4。还有一个问题是弹出1时栈中没有元素，无法计算宽度，所以在初始化时要在栈底加一个-1来应对所有元素都出栈的情况。
代码
class Solution(object):
def largestRectangleArea(self, heights):
""" :type heights: List[int] :rtype: int """
stack=[]
i=0
area=0
while i<len(heights):
if stack==[] or heights[i]>heights[stack[len(stack)-1]]: # 递增直接入栈
stack.append(i)
else: # 不递增开始弹栈
curr=stack.pop()
if stack == []:
width = i
else:
width = i-stack[len(stack)-1]-1
area=max(area,width*heights[curr])
i-=1
i+=1
while stack != []:
curr = stack.pop()
if stack == []:
width = i
else:
width = len(heights)-stack[len(stack)-1]-1
area = max(area,width*heights[curr])
return area
总结
stack.pop()输出弹出的值
京公网安备 11010502036488号