最长回文子串——Manacher 算法

1.问题描述

给定一个字符串，求它的最长回文子串长度。

示例 1：

输入: "babad"
输出: 3

示例 2：

输入: "abc1234321ab"
输出: "7"

2.Manacher 算法原理

回文半径

我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径。

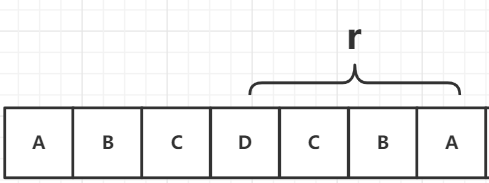
Gur7yF.png

如上图,以D为中心，"ABCDCBA"构成一个一个回文串，那么该回文串的回文半径就是r。

预处理

Manacher算法首先会进行一个预处理，在字符串的所有空隙位置(包括首尾)插入同样的符号，要求这个符号是不会在原串中出现的。例如将字符串"ABBACDC"转换为"#A#B#B#A#C#D#C#"。然后，我们会发现"ABBA"偶回文和"CDC"奇回文分别被转换成了"#A#B#B#A#"和"#C#D#C#"，都变成了奇回文，这就解决了长度奇偶性带来的对称轴位置问题。

我们还定义了一个rec数组，用于记录以i为中心的最大回文半径，如表

i 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
s_new # A # B # B # A # C # D # C #
rec[i] 1 2 1 2 5 2 1 2 1 2 1 4 1 2 1

从表中不难得到，的最大值即为原字符串的最长回文子串长度。那么我们怎么来求数组呢？

case1：

在这里插入图片描述

为关于中心（或对称轴）C的对称点，那么，我们由回文串（以为对称轴，为回文半径）的性质可得，到部分的字符串=到部分的字符串。由回文串（以为对称轴，为回文半径）的性质可得，到部分的字符串=到部分的字符串。由回文串（以为对称轴，为回文半径）的性质可得，到部分的字符串=到部分的字符串。因此，到部分的字符串=到部分的字符串=到i部分的字符串=到部分的字符串。所以，此时以为中心的最大回文半径为（即）。

case 2:

在这里插入图片描述

此时到部分的字符串与到部分的字符串相交，但很容易得到二者仍然相等，然后其余的与case1同理，易得此时以为中心的最大回文半径为（即）。

case 3:

在这里插入图片描述

与case1同理,但是由于到部分的字符串超过了回文串（以为对称轴，为回文半径）的界限（即），所以，此时以为中心，回文半径至少为，然后还要继续扩展回文串，直到左右两边字符不同，或者到达边界。

case 4:

在这里插入图片描述

此时到部分的字符串与到部分的字符串相交，但很容易得到二者仍然相等，然后其余的与case3同理，易得此时以为中心,回文半径至少为，然后还要继续扩展回文串，直到左右两边字符不同，或者到达边界。

case 5:

当在的右边时，说明以为对称轴的回文串还没有被访问过，于是只能从的左右两边开始扩展，直到左右两边字符不同，或者到达边界。

结论：

伪代码如下：

如果i<right_border且rec[2*center-i]<right_border-i+1
{
    rec[i]=rec[2*center-i];
}
如果i<right_border且rec[2*center-i]>=right_border-i+1
{
    rec[i]=right_border-i+1
    继续扩展回文串，直到左右两边字符不同，或者到达边界
}
如果i>=right_border
{
    rec[i]=1;
    继续扩展回文串，直到左右两边字符不同，或者到达边界
}
如果right_border<i+rec[i]-1
    更新right_border和center

具体代码如下：

if(i<right_border)
    rec[i]=min(rec[2*center-i],right_border-i+1);
else
    rec[i]=1;
while(i-rec[i]>=0&&rec[i]+i<len_new&&s_new[rec[i]+i]==s_new[i-rec[i]])
    rec[i]++;
if(right_border<i+rec[i]-1)
{
    right_border=i+rec[i]-1;
    center=i;
}

3.时间复杂度分析

从上面的分析中，可以看出，算法只有遇到还没有扩展过的位置时才进行扩展，已经扩展过的位置不会再继续进行扩展，所以对于进行预处理过的字符串中的每一个位置，只会进行一次扩展，所以虽然Manacher算法有两层循环，但是Manacher算法的总体时间复杂度为，即。

4.算法实现

#include <iostream>
#include <cstring>
using namespace std;
char s[10001],s_new[30007];
int rec[30007];


void init()
{
    int len=strlen(s);
    int cnt=0;
    s_new[cnt++]='#';
    for(int i=0;i<len;i++)
    {
        s_new[cnt++]=s[i];
        s_new[cnt++]='#';
    }
    s_new[cnt]='\0';
}


int Manacher()
{
    int len_new=strlen(s_new);
    int right_border=0,ans=-1,center;
    for(int i=0;i<len_new;i++)
    {
        if(i<right_border)
            rec[i]=min(rec[2*center-i],right_border-i+1);
        else
            rec[i]=1;
        while(i-rec[i]>=0&&rec[i]+i<len_new&&s_new[rec[i]+i]==s_new[i-rec[i]])
            rec[i]++;
        if(right_border<i+rec[i]-1)
        {
            right_border=i+rec[i]-1;
            center=i;
        }
        ans=max(ans,rec[i]-1);
    }
    return ans;
}


int main()
{
    while(cin>>s)
    {
        init();
        cout<<Manacher()<<endl;
    }
    return 0;
}

5.相应练习

力扣：https://leetcode-cn.com/problems/longest-palindromic-substring/

牛客：https://www.nowcoder.com/questionTerminal/b4525d1d84934cf280439aeecc36f4af