读前福利:几百本经典书籍 https://www.johngo689.com/2158/
原文链接:https://www.johngo689.com/2264/
LeetCode 刷题的进展有段时间没有更新了,过去的一篇文章有过这方面的解释,今天再来说一下。
穿插一句,今天文末再送书哈...
回归正题:
两点原因,第一点就是有读者说过去文章太长,是否可以考虑截取出来,分类讨论。这一点我是有考虑的,事实上本身文章已经是一个类别了,比如说动态规划,整个介绍超过万字,自我感觉才把一个问题描述的比较清楚。所以,后面考虑再细分,使得想要表述的问题更加调理清楚,可读性更强。
另外一点原因呢,就是关于文章页面展示。也是关于一个可读性的方面,这个是真真切切花了将近一个月搞的一个事情。就是重新打理了一个网站(www.johngo689.com,感觉还是比较漂亮的,每天都要看几眼、、哈哈)。
这中间还有人问到为什么域名起这样的一个名字,还穿插着数字,咱们还是后面有空在说说(later。。。)
今天咱们一起要讨论的是关于「字符串」的第一块内容。
字符串 - 滑动窗口
今天再把整个的刷题脑图放出来,前面的已经细化,后面一块一块逐渐会整理出来。
可以看在整个大的脑图当中**「字符串 - 滑动窗口」**这一块。

上面是整个 LeetCode 算法刷题计划,图中只细化了二叉树、动态规划和字符串相关理论分析和题目的讲解。所以,没有加入的同学们可以私信我,即使现在没有计划刷题的也可以加入进来,当个看客也不错,身处互联网,迟早会用到。
之前说到过,「字符串」这一块会出 10 篇复盘总结,今天是第一篇「字符串 - 滑动窗口」。
**「字符串 - 滑动窗口」**这一块咱们安排了四个问题,准备用这四个问题将滑动窗口的使用以及相关题目讨论清楚。
【简单】滑动窗口数字之和(引例)
【中等】567.字符串的排列 https://leetcode-cn.com/problems/permutation-in-string/
【困难】239.滑动窗口最大值 https://leetcode-cn.com/problems/sliding-window-maximum/
【中等】3.无重复字符的最长子串 https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/
滑动窗口-引例
滑动窗口算法一般是作用在字符串或者数组上,通过不断的滑动逻辑窗口,在特定窗口大小内进行计算的过程。
滑动窗口的方式可以降低时间复杂度,从而减短计算的执行时间。
引例:比如说在字符串 s="5189623196" 中,窗口大小 w=5,找出每个窗口字符子串的和。
普通的计算方式:每 5 个进行一次求个计算,时间复杂度方面能够达到 O(N^2)。
利用窗口的方式:可很大程度可以减小时间方面的消耗。就拿引例来说,时间复杂度应该是O(N)的线性复杂度。
该案例核心思路是:窗口在每一次的滑动前后,中间元素内容没有改变,仅仅改变的是开头和结尾元素。
即:下一窗口内元素之和 = 上一窗口元素和 - 离开窗口元素值 + 新加入窗口元素值
下面分步骤进行讨论,将最终结果写入到 res 中。
步骤一:直接计算窗口内元素和,res = [29]

步骤二:在上一步骤的基础上,减去离开窗口的元素,加上新加入窗口的元素。

步骤三:继续在上一步骤的基础上,减去离开窗口的元素,加上新加入窗口的元素

相同逻辑继续执行....
步骤六:滑动窗口将最后一个元素包含进来

上述每一步骤中,将 sum 值都添加到最终的结果变量 res 中。
滑动窗口这样的思维方式就很巧妙的进行在窗口的不断移动,进而产生各元素在窗口边界进进出出,利用这一点,在时间复杂度方面进行了一个很大提升!
代码简单的写一下,还是利用 Python,也是因为 Python 的话,绝大多数人还是比较熟悉。
class Solution(object):
def sumSlidingWindow(self, s, w):
sum = 0
res = []
# 计算第一个窗口数字之和
for item in range(5):
sum += s[item]
res.append(sum)
# 后面利用滑动窗口思想进行计算
for item in range(w, len(s)):
sum -= s[item-w]
sum += s[item]
res.append(sum)
return res
下面咱们用三个 LeetCode 经典案例进一步阐述滑动窗口这类题目。
滑动窗口经典题目
567.字符串的排列【中等】
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。
换句话说,s1 的排列之一是 s2 的 子串 。
输入:s1 = "ab" s2 = "eidbaooo" 输出:true 解释:s2 包含 s1 的排列之一 ("ba").
首先,两个字符串的排列,首先可以想到字典,根据字典去比较。
词典可根据两个不同字符串将给到的字符进行计数,因此,这样很同容易进行比较。
另外,在遍历 s2 的时候,使用滑动窗口,该窗口的长度是字符串 s1 的长度,遍历 s2 使得字符不断的出入,在此过程中比较两个字典。
整个过程,记 s1 的长度为 size1,s2 的长度为 size2,窗口大小为 size1,不断遍历 s2,直到 s2 的结尾。
记 s1 的字典为 dict_s1,记s1的字典为dict_s2,在遍历s2的过程中,每滑动一次窗口,比较 dict_s1 和 dict_s2 是否相等。
窗口滑动过程中,需要删除滑出窗口的元素以及新增滑入窗口的元素。
删除滑出窗口的元素:广义上是从字典 dict_s2 中删除,注意此处不能直接删除,因为可能会有重复元素存在,比如:{'a':2},所以只能是将 value 值减 1。之后再判断 value 值为否为 0,如果为 0 了,这个时候就可以直接将该元素从字典中删除。
新增滑入窗口的元素:直接将滑入窗口的元素添加进字典中。
下面用几个图清晰的一步一步操作:
初始化 s1 对应的字典 dict_s1={'a':1,'b':1}
① s2 对应的字典为图中窗口中的元素 dict_s2={'e':1,'i':1}。
最后判断 dict_s1 != dict_s2

② 向右滑动窗口,由于元素e的 value 值为 1,直接删除该元素,加入新元素d,此时,dict_s2={'i':1,'d':1}。
最后判断 dict_s1 != dict_s2

③ 继续向右滑动窗口,由于元素 i 的 value 值为 1,直接删除该元素,加入新元素 b,此时,dict_s2={'d':1,'b':1}。
最后判断 dict_s1 != dict_s2

③ 继续向右滑动窗口,由于元素 d 的 value 值为 1,直接删除该元素,加入新元素 a,此时,dict_s2={'b':1,'a':1}。
最后判断 dict_s1 == dict_s2 ,此时可以直接返回 True。不用在继续窗口滑动了。

这个题虽然在 LeetCode 中标记为中等,但是用滑动窗口的方式去解决还是非常容易理解的。
下面是 Python 代码的实现:
class Solution(object):
def checkInclusion(self, s1, s2):
size1 = len(s1)
size2 = len(s2)
if size1 > size2:
return False
dict_s1 = collections.Counter(s1)
dict_s2 = collections.Counter(s2[:size1-1])
left = 0
for right in range(size1-1, size2):
# 增加新添加的元素
dict_s2[s2[right]] += 1
# 判断如果字典相同,则返回 True
if dict_s1 == dict_s2:
return True
# 删除左边剔除的元素(首先需要将左边元素的 value 值减 1)
dict_s2[s2[left]] -= 1
# value 值为 0 的时候,就可以删除该元素了
if dict_s2[s2[left]] == 0:
del(dict_s2[s2[left]])
# 窗口整体向右移动一格
left += 1
right += 1
return False
下面再看一个稍微复杂一点的,也是滑动窗口的典型例题。
239.滑动窗口最大值【困难】
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
滑动窗口最大值是一道典型的滑动窗口的例题。该题被标记为困难,可能就在于最大值的判断,如果使用传统方式的话,时间复杂度就会很高。
关于最大值,可是尝试使用优先队列去解决,即构造大顶堆,也可以使用双向队列解决问题。
以下用两种方式都来解决一下。
方法一:优先队列解决
由于题目要求是选择窗口内的最大值,因此需要构造了大顶堆,此时得出来队首元素就是整个队列的最大值。
注意点:我们这里由于采用 Python 的 heapq 库来实现,而 heapq 库只能构造小顶堆。
因此,可以换一个思路进行实现,例如列表 [1,-3,12]:
首先,每个元素的负值都插入到优先队列中,构造小顶堆,产生的结果是这样的 [-12, 3, -1]
然后,将队首元素去除并且取反,得到的结果是 12。这就是我们想要的结果,取到了其中的最大值。
关于 Python 使用优先队列的方式,可以查看这一篇文章【https://mp.weixin.qq.com/s/94Rnnt7R5_kTfoAW0j-wyQ】,有详细的使用方式。
首先,初始化一个窗口大小的优先队列 window,并且记录元素(注意这里要取反)以及元素下标,组装成一个元祖 (-num, index)。
然后,当不断向右移动窗口,把新加进来的元素(元祖)加入到优先队列中。
最后,判断当前优先队列中的队首元素对应的 index,是否在固定窗口内,如果在,则取值并且取反;否则,删除队首元素,继续判断。
下面依旧用几个图清晰的一步一步操作:
我们用字符串为 nums=[12, -3, 1, -1, 9, 5], k = 3 来进行说明。
初始化 res 用来存储每个窗口最大值。
① 初始化优先队列 window=[(-12, 0), (3, 1), (-1, 2)],判断队首元素的下标值 value=0 在当前窗口内。
所以,取出队首元素-12,并且取反,res=[12]
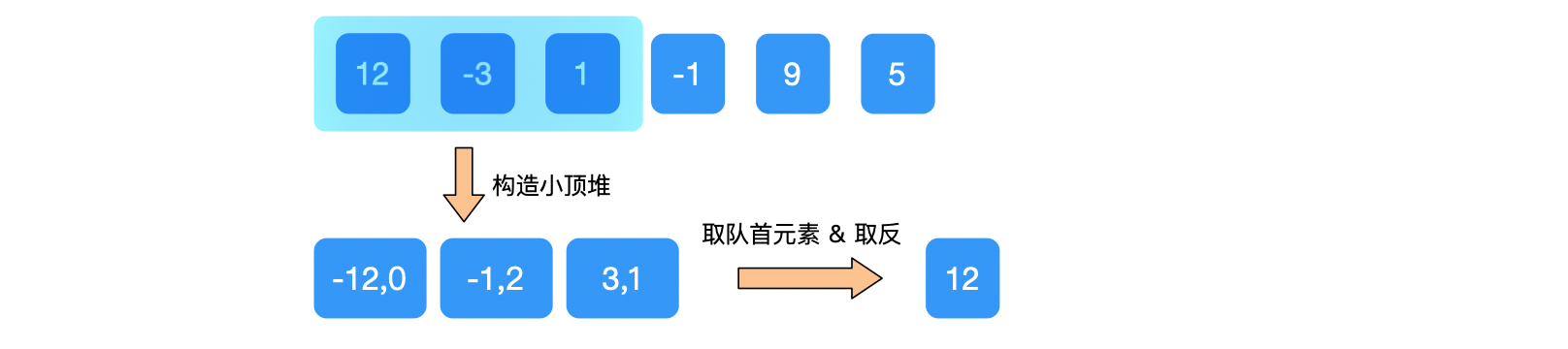
② 优先队列 window=[(-12, 0), (-1, 2), (1, 3), (3, 1)],判断队首元素的下标值 value=0 不在当前窗口内,弹出队首元素。
此时,window=[(-12, 0), (-1, 2), (1, 3), (3, 1)],再判断此时队首元素的下标值 value=2 在当前窗口内。
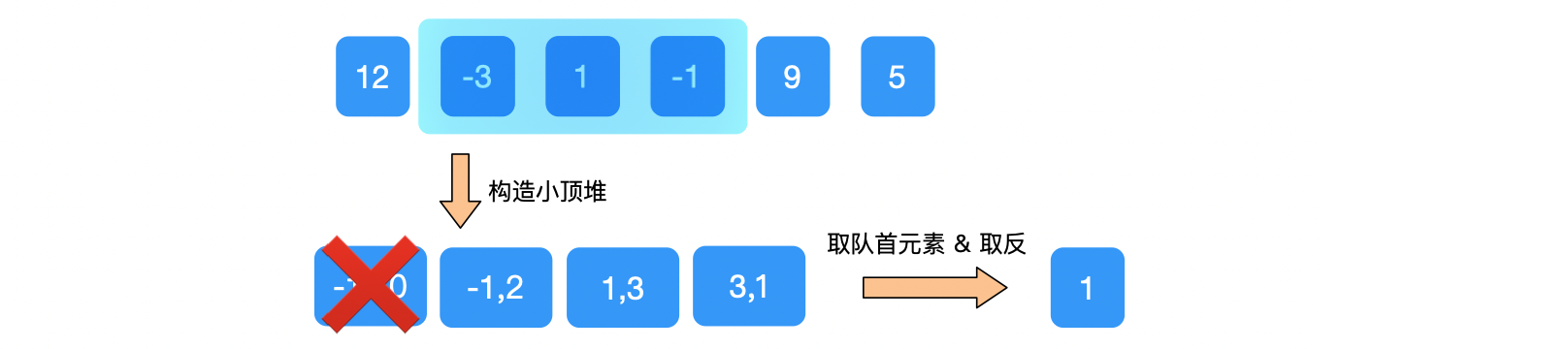
所以,取出队首元素-1,并且取反,res=[12, 1]
③ 优先队列 window=[(-9, 4), (-1, 2), (3, 1), (1, 3)],判断队首元素的下标值 value=4 在当前窗口内。
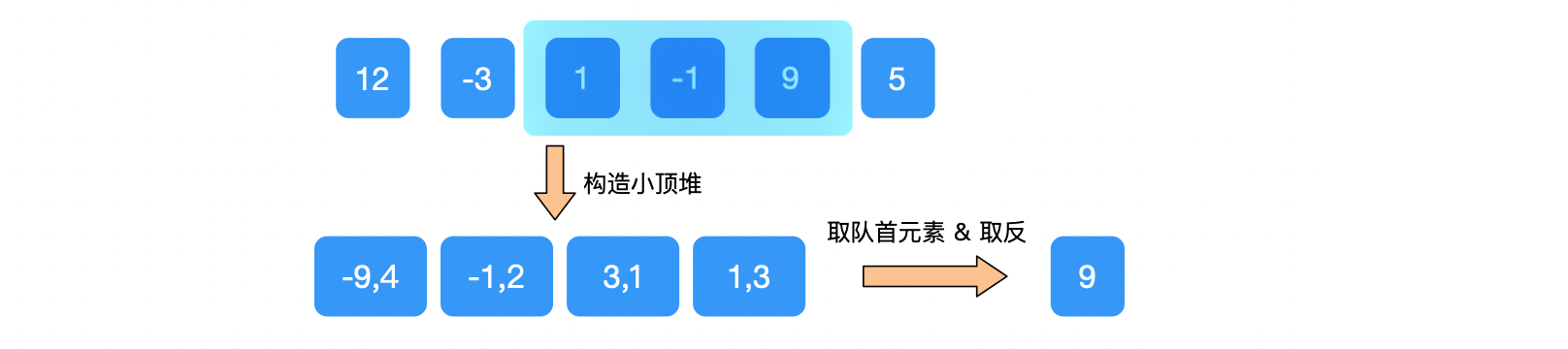
所以,取出队首元素-9,并且取反,res=[12, 1, 9]
④优先队列 window=[(-9, 4), (-5, 5), (3, 1), (1, 3), (-1, 2)],判断队首元素的下标值 value=4 在当前窗口内。
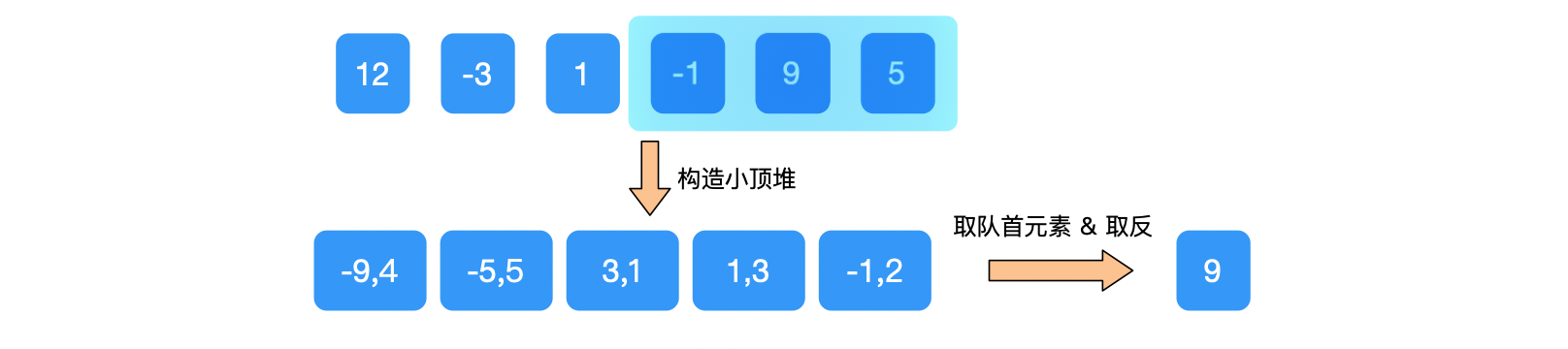
所以,取出队首元素-9,并且取反,res=[12, 1, 9, 9]
这个时候就都所有取数完成了!
中间关于 Python 的 hepq 库构造大顶堆有点绕,这点稍微理解下,对于后面的解题帮助特别大。
思路描述完了,再看下代码实现:
def maxSlidingWindow(self, nums, k):
size = len(nums)
window = [(-nums[i], i) for i in range(k)]
heapq.heapify(window)
res = [-window[0][0]]
for i in range(k, size):
heapq.heappush(window, (-nums[i], i))
while window[0][1] <= i-k:
heapq.heappop(window)
res.append(-window[0][0])
return res
感觉描述了一堆,但是代码倒是很简洁。
说完方法一,下面看看方法二...
方法二:双向队列解决
为什么要使用双向队列呢?在算法执行过程中,需要两边进行入队和出队的操作。
大致思路也比较容易:
首先,初始化一个空队列 queue;
然后,逐个入队,但当下一个元素入队时,判断与队尾元素大小。如果小于队尾元素,则入队。否则,队尾依次出队,直到大于要入队的元素;
最后,判断队首元素是否是在窗口内,如果在窗口内,直接取值,否则,队首元素出队。
下面依旧用几个图清晰的一步一步操作:
① 元素 12 入队;窗口范围 [0, 0]
未形成窗口,不取值;
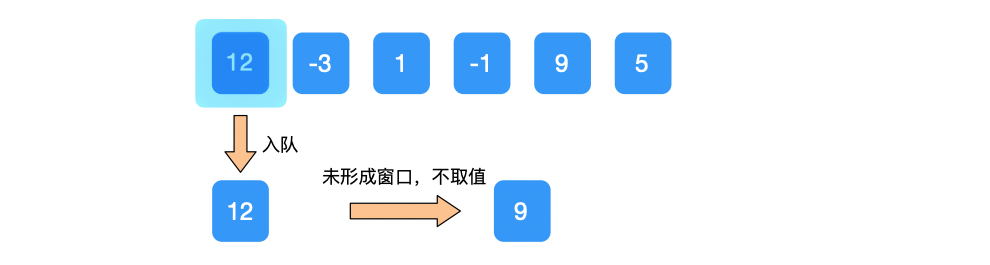
② 元素 -3 入队;窗口范围 [0, 1]
比队尾元素 12 小,直接入队;
未形成窗口,不取值;
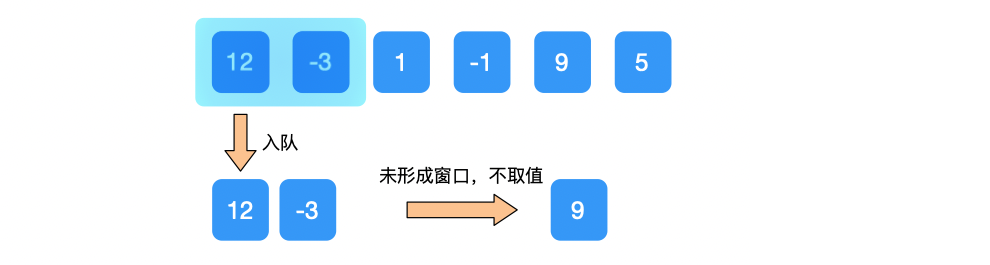
③ 元素 1 入队;窗口范围 [0, 2]
比队尾元素 -3 大,所以,队尾元素出队,元素 1 入队。而且队首元素12 下标0在窗口内
取队首元素 12;
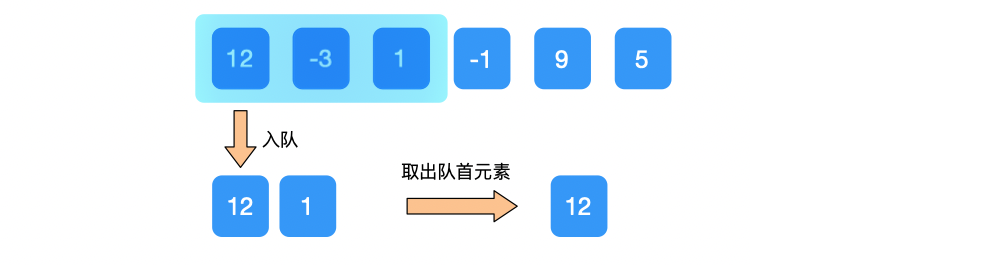
④ 元素 -1 入队;窗口范围 [1, 3]
比队尾元素 1 小,元素 -1 入队。队首元素12 下标 0 不在窗口内,元素 12 出队;取队首元素 1 的下标 2 在窗口内;
取队首元素 1;

⑤ 元素 9 入队;窗口范围 [2, 4]
比队尾元素 -1 和 1 都大,所以,比他小的队尾元素均出队,元素 9 入队。而且队首元素 9 下标4在窗口内
取队首元素 9;

⑤ 元素 5 入队;窗口范围 [3, 5]
比队尾元素 9 小,元素 5 入队。而且队首元素 9 下标4在窗口内
取队首元素 9;

利用双向队列的方式也将窗口内最大元素取出来了!
上面是整体的思路,具体到代码中,是把进入队列的元素替换为元素的下标,这样实现起来更加容易!
看下 Python 代码的实现:
class Solution(object):
def maxSlidingWindow1(self, nums, k):
size = len(nums)
queue = collections.deque()
res = []
for i in range(0, size):
# 新元素进队,在队不空的情况下,需要判断与队尾元素的大小
while queue and nums[i] > nums[queue[-1]]:
queue.pop()
queue.append(i)
# 在已经形成窗口(i+1>=k)的前提下,判断队首是否在窗口内
while queue[0] < i-k+1:
queue.popleft()
# 从形成窗口的时刻开始将元素置于结果集 res 中
if i+1 >= k:
res.append(nums[queue[0]])
return res
无论是利用优先队列还是双向队列,都需要注意所取的元素是否在当前的窗口内。
3.无重复字符的最长子串【中等】
给定一个字符串
s,请你找出其中不含有重复字符的 最长子串 的长度。输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
想要判断字符是否存在,通常会使用到字典结构来判断是否存在。
首先,初始化窗口左右端 left=0 和 right=0,初始化字典 words 用来存放已加入字符的元素(key)和元素下标(value),例如,words={'a':0,'b':1,'c':2}
然后,right 指针向右移动,判断新加入元素是否存在于字典中,如果存在,让窗口左边界指向字典对应 value 值的下一个位置,并且更新字典中对应元素的下标值(value);如果不存在,则加入字典 words 中;
注意点:
中间有可能 left 已经更新到后边,而新判断的元素可能在前面,会导致 left 变小,所以需要采用 max 来进行判断
举例:abba,执行到第二个 b 的时候,left=2,此时words={'a':0,'b':2}。后面再判断最后的 a 的时候,就会使得 left=0+1=1
因此,需要 left = max(words.get(v) + 1, left)
最后,每一步骤记录最长子串长度。
依旧用几个图清晰的一步一步操作:
① left=0, right=0, 加入新元素 'a',words={'a':0}, 窗口长度为1

② left=0, right=1, 加入新元素 'b',words={'a':0, 'b':1}, 窗口长度为2

③ left=0, right=2, 加入新元素 'c',words={'a':0, 'b':1, 'c':2}, 窗口长度为3

④ left=0, right=3, 加入新元素 'a';
发现 a 已经在 words={'a':0, 'b':1, 'c':2} 存在;
则更新 left=max(words.get('a') + 1, left)=1,words={'a':3, 'b':1, 'c':2}
窗口长度为3

⑤ left=1, right=4, 加入新元素 'b';
发现 'b' 已经在 words={'a':3, 'b':1, 'c':2} 存在;
则更新 left=max(words.get('b') + 1, left)=2,words={'a':3, 'b':4, 'c':2}
窗口长度为3

⑥ left=2, right=5, 加入新元素 'c';
发现 'c' 已经在 words={'a':3, 'b':4, 'c':2} 存在;
则更新 left=max(words.get('c') + 1, left)=3,words={'a':3, 'b':4, 'c':5}
窗口长度为3

⑦ left=3, right=6, 加入新元素 'b';
发现 b 已经在 words={'a':3, 'b':4, 'c':5} 存在;
则更新 left=max(words.get('b') + 1, left)=5,words={'a':3, 'b':6, 'c':5}
窗口长度为2

⑧ left=5, right=7, 加入新元素 'b';
发现 'b' 已经在 words={'a':3, 'b':6, 'c':5} 存在;
则更新 left=max(words.get('b') + 1, left)=7,words={'a':3, 'b':7, 'c':5}
窗口长度为1
左右步骤描述完毕!
根据每一步骤记录的窗口长度,可得到最长窗口为 3。
下面就由上述逻辑得到最终的代码:
class Solution(object):
def lengthOfLongestSubstring(self, s):
if not s:
return 0
left, right = 0, 0
length = 1
words = {}
for right, v in enumerate(s):
if s[right] in words.keys():
print(words.get(v) + 1, left)
left = max(words.get(v) + 1, left)
length = max(right-left+1, length)
# 将当前值的 value 值覆盖
words[v] = right
print(words)
return length





 京公网安备 11010502036488号
京公网安备 11010502036488号